 Sign numbers |
Multiple precision |
Floating point |
| Footer |
Procedures Employed in Digital Systems :
6. - PROCEDURES EMPLOYED IN DIGITAL SYSTEMS
Digital systems, when they are wired or programmed to perform certain functions, perform their task whenever they are solicited and this indefinitely (or almost), without fatigue, weariness and very high speed.
They can repeat long, error-free procedures, with only those initiatives that the technician will have planned in their programming.
These systems are therefore disciplined but without imagination, which implies that the procedure to be followed will be indicated with order and method ; each step will have to be dictated and shelled.
It appears that the technician must have a perfect knowledge of the problem that his machine will have to deal with alone afterwards.
In the case that interests us for the moment, it would be desirable to find a universal procedure for carrying out these operations and depending on the operator (designation of the operation), certain steps could be made transparent.
If this solution may seem long, we know that this does not really present a big disadvantage, given the speed at which these calculations are made (except for special cases: ballistics calculations ... where the speed of calculation is paramount).
The register
Before approaching these methods, it is necessary to specify some points. On this subject, we will impinge on the rest, speaking of register.
When one wishes to perform an operation whose result can not be found mentally, one takes a sheet of paper and one inscribes the numbers there : one poses the operation.
If we are called to another urgent task at this time, it is completed, we return to our sheet of paper on which we find the numbers previously recorded.
There is memorization of information.
If we enter information in a digital machine, using a keyboard, before making transformations on this information, we must store them, put them in memory.
In these machines, these memories are registers (etymologically, a register is a book in which one records facts or acts of which one wants to keep the memory).
The elementary information in binary is the "bit" (binary - digit = chiffre binaire). This information is either 0 or 1, which, in positive logic, results in the absence or the presence of a voltage.
Consequently, the elementary cell of a register must be able to keep in memory definitively, if no external action intervenes, either an absence of tension (level 0), or the presence of a tension (defined as being equal to level 1).
In fact, it stores the numerical value of the bit.
We know that decimal numbers (language of the human being) when expressed in binary (machine language) use a larger number of weights, and therefore, their writing is longer.
For example, if you want to enter numbers in the machine whose numeric value does not exceed 255, it will take eight elementary cells of register in binary whereas it would be necessary three in decimal.
In summary, a register is a memory in which binary numbers can be stored. One of their main characteristics, is the maximum numerical value that they can memorize, one also speaks of capacity or length of the register.
You will learn in the next lessons devoted to these registers, how we enter this information, how they stay and how we access it.
For now, admit that it is possible.
These registers are very important because they condition the computing capacity of the system. Imagine that our sheet of paper is not big enough to fit numbers of more than three numbers, we understand that the calculations will quickly be limited.
6. 1. - SIGNED NUMBERS
On the other hand, we know that a number is characterized by its absolute numeric value and its sign.
We must find a method that binds a sign to the binary numeric value.
We will now describe the methods considered :
The first is to put in front of the absolute value of the number a bit of sign.
For a positive number, the sign bit is 0. If it is negative, the sign bit is 1.
Example :
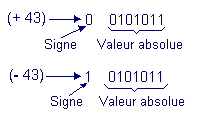
The number (+ 43), according to the signed binary representation is noted :
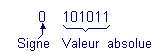
The number (- 43) is noted :
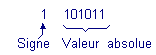
In the case of a digital system, for example a pocket calculator, the length of the registers is defined and immutable. If they consist of eight cells, the representation of these numbers is as follows :
This method tends to be abandoned in favor of that of the complement to 2 that we describe below.
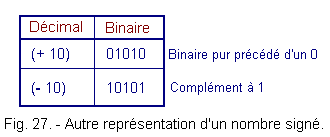
The second method that was used, does not use the sign bit in the same way.
Positive numbers are represented with a 0 at the most significant digit.
Negative numbers are represented by the complement to 1 of the corresponding positive number.
The complement intervenes on the bit of sign, one finds, consequently, a 0 for a positive number and a 1 for the negative numbers, with the most significant figure.
An example is given in Figure 27.
This system is also abandoned because it presents a disadvantage of size : the double expression of 0.
Indeed, if one counts positive values towards 0, this one will have for expression 0. If one counts down negative values towards 0, this one will have for expression 1.
Figure 28 clearly demonstrates this.
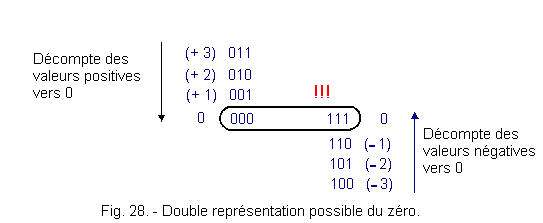
This method creates an ambiguity that digital systems can not accommodate without the use of subterfuges.
The third method, which is becoming generalized, is based on the complement to 2 (see chapter 4. 3. 4. on the complement to 2).
It consists, for the positive numbers in their representation in pure binary preceded by a 0.
Their opposites, in negative values, are represented by the complement to 2.
The complementation also intervenes on the sign bit and the negative numbers are preceded by a 1.
Example :
-
The number (+ 10) is represented by : 01010
-
The number (- 10) is represented by : 10110
As shown in Figure 29.
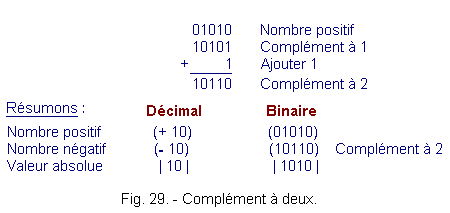
This representation of the negative binary numbers, by the complement to 2 does not pose the ambiguity of the double expression of the zero and will serve us in the procedure of obtaining the result for the operations carried out by the machine.
The use of relative numbers imposes a decrease of the capacity of the registers, since a cell will be reserved for the sign.
Figure 30 represents some of the relative numbers between (+ 127) and (- 128) used in digital machines whose registers comprise eight elementary cells, thus capable of storing eight-bit words, called bytes.
It is necessary during the discussions to specify the method used for the representation of negative numbers, this is obvious.
Similarly, we must not forget to precede a 0 positive numbers. These two points are very important.
6. 2. - MULTIPLE PRECISION
We talked about eight-bit words or bytes. In digital systems, a word, whatever the number of bits, can take the name of «byte» (Anglo-Saxon term).
We have just seen that with one byte, it was possible to represent 256 values (+ 127 to - 128 including 0).
It is obvious that for the majority of the calculations, it is very insufficient. It is therefore necessary to resort to an artifice.
The number of cells in the registers can be extended, but this leads to some problems with integrated circuits.
It is also possible to use several times eight bits. For example, if the numbers are double-byte, 65 536 numerical values can be represented, which represents the relative numbers from (+ 32 767) to (- 32 768) through 0.
The number thus represented consists of twice eight bits, the eight least significant bits constitute the least significant word (M.M.S.) and the eight most significant bits, the most significant word (M.P.S.).
The least significant octet (O.M.S.) and the most significant octet (O.P.S.) are also said. This way of proceeding using several bytes, takes the name of multiple precision.
When using only two bytes, we will say that it is double precision.
In calculating machines, this resolution is not yet sufficient. We use several words or several bytes (the words are not necessarily organized in bytes).
According to the desired resolution, one is led to use three or four words, so the precision is clearly sufficient.
This procedure is called : multiple precision.
The multiple precision increases the time of obtaining the result, because the machine, to make the calculations must call M.M.S. (least significant words), carry out the operation with these, store the result and report, if it exists, then call the following words, perform the calculations.
It is easy to understand that if the procedure is longer, the result is obtained a little later.
For a binary number, as well as in decimal (we discussed this in Chapter 1), the figure with the highest weight rank is named : the most significant bit or B.L.P.S.
On the other hand, the one with the lowest rank : the least significant bit or B.L.M.S.
6. 3. - THE FLOATING VIRGUL
Until now, we have only spoken about integers, we must also be able to represent fractional numbers and, in some cases, very large numbers.
The floating point is none other than the exponential notation (or scientific notation) and it solves the problem of representing very small numbers with very large numbers.
These procedures, multiple precision and floating point, will be useful when you approach microprocessors.
For the moment, they are described for the record and because they normally fit into this lesson.
In the decimal system, it is the notation using the powers of 10.
This notation consists of a part which is called the mantissa and a second which is called the exponent.
The exponent is none other than the weight of the rank occupied by the integer part of the mantissa.
Example :
0,00015 writes : 1,5 x 10-4
0,005 writes : 5 x 10-3
1246 writes : 1,246 x 103
We can also use the following convention by using the same examples :
0,00015 Þ 0,15 x 10-3
0,005 Þ 0,5 x 10-2
1246 Þ 0,1246 x 104
All these numbers start with 0 and since they all come from the power of 10, we can very well adopt the following writing system :
0,15 x 10-3 Þ (+ 15) (- 3)
0,5 x 10-2 Þ (+ 5) (- 2)
0,1246 x 104 Þ (+ 1246) (+ 4)
The Mantissa M is always less than 1 and equal to or greater than 0,1 :
0,1 £ M < 1
In digital systems and especially with microprocessors, it is not the power of 10, but the power of 2, since we work in binary.
In these systems using words of eight bits or bytes, this form of writing can be preserved by assigning a word for the mantissa and a word for the exponent.
In the numerical example, we see that with a byte, we will not be able to represent the numerical value 1246, especially if we use the method of the complement to 2 for the negative values because it remains then only seven bits to express this numerical value.
By using multiple precision, that is by working on several bytes, this becomes possible.
If for example we use three bytes for the mantissa and its sign, and a byte for the exponent and its sign, we can represent the relative numbers within the following limits :
(+ 223 - 1) x 2127 to (- 223) x 2127
Either in decimal :
± 0,142 x 1046 or, ± 142 followed by 43 zeros.
Values as small as (± 1) x 2-127 can be represented, either in decimal :
± 0,58 x 10-38 or, ± 0, ... 38 zeros ... 58.
This way of writing the numbers, keeping the memory of the location of the decimal point, allows the calculations on very large or very small (fractional) numbers.
To summarize, in numerical systems intended for computations, we use for the representation of relative numbers, the complement to 2 for negative numbers, the multiple precision and the exponential notation or floating point.
If we use four bytes, three for the mantissa and one for the exponent, all the numbers will be represented by the same number of bytes, that is to say they will all have the same format.
Is :
-
for the exponent 7 bits Þ 127 (decimal) plus the sign : ± 127, therefore 2± 127
-
for the mantissa 23 bits plus one for the sign, which corresponds to : ± 223
Floating operations are subject to a special procedure.
The multiplication does not pose any difficulty, one multiplies the mantissas between them and one adds the exponents.
The addition requires a resetting operation which consists in making the exponents equal in absolute value, which is imperative in this case, since one must add only numbers of the same weight.
We will not go into these details any more and know that there are integrated circuits specially designed for floating point operations.
 Click here for the next lesson or in the summary provided for this purpose. |
 Haut de page |
|
Previous Page |
 Next Page |
Nombre de pages vues, à partir de cette date : le 27 Décembre 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.