Complement of a numberReminders on Basic Operations :
4. - VALUE, SIGN, COMPLETION OF A NUMBER
With numeration, we have seen the numbers and the most common way of organizing them to make up the numbers.
However, it remains to specify certain terms relating to these numbers.
4. 1. - ABSOLUTE DIGITAL AVALEUR
The absolute numerical value is one of the possible determinations of a variable quantity.
We have seen that in position numeration, each graphic used has a meaning in itself, and according to its rank in the order of writing the number, it is assigned a fixed weight.
This double "weighing" constitutes the absolute numerical value of the number.
4. 2. - NUMBER SIGN
The absolute value of a number is preceded by the sign + (plus), when this number is greater than zero.
In the case where this number is less than zero, the absolute value is preceded by the sign - (minus).
The numbers accompanied by the + sign will be called : positive numbers.
Those preceded by the sign - include : negative numbers.
The set of positive and negative numbers is called the set of relative numbers.
By convention, positive numbers are not represented with their + sign.
To summarize :
an absolute value number : |256|
an positive number : + 256 or 256
an negative number : - 256.
For greater precision, and in order to separate the sign from the number and from the operations that can be performed with the relative numbers, the latter should be represented by their absolute value and their sign in parentheses.
Example : (+ 256),
(- 128).
In the current calculations, for simplification, the parentheses are omitted.
The complement of a number is the number that must be added to the first to obtain a third, designated in advance and serving as a kind of reference.
Example :
The complement of the number 75 with respect to the numerical value 87, designated in advance is :
87 - 75 = 12
The importance of the complement to an arbitrary value (as in this example : 87) is not obvious except in the case of subtraction.
On the other hand, there are special cases, such as add-ons to 9 or 10 (in decimal system), as well as add-ons to 1 or 2 (in binary system), which will be used for carrying out operations in systems numerically (subtraction and division).
Obviously, in these systems that use the binary number, it is the 1 and 2 complements, but for a better approach to this process, we will start with the supplements in the 10-based count.
4. 3. 1. - COMPLEMENT Consider a number, consisting of n digits, the complement to 9 of this number is the one which is composed of the sequence obtained by the subtraction of each of these n digits, from the digit 9.
Example :
999 - 128 = 871
871 is the complement to 9 of the number 128.
It is necessary, therefore, to understand by complement to 9, the complement of each digit making up this number in relation to 9.
This term is intended to define the numerical value that must be added to a designated number to obtain the power immediately greater than this number, in the base used, minus the
Example :
Take the number 128.
The power or rank value, immediately greater than this number, in the base 10 is :
The higher power minus the unit is :
1000 - 1 = 999
The complement to this value is :
999 - 128 = 871
The complement to 9 has the following particularity :
4. 3. 2. - COMPLEMENT A 10
Again, it is a word that is intended to define the numerical value that must be added to a designated number to obtain the power immediately greater than this number, in the base used.
Therefore, it is the complement to 9 to which 1 is added.
Example :
Let's find the complement to 10 of the number 128.
Other way :
Let's take the complement to 9 previously obtained and add 1 :
871 + 1 = 872
872 is the complement to
10
of 128.
Figures 11-a and 11-b show the complements at 9 and 10 for the numbers from 1 to 9.
4. 3. 3. - LE COMPLEMENT A 1
It is no longer a question of the decimal system but of the binary system.
The complement to 1 is the binary equivalent of the complement to 9 decimal.
The number 9 is the last graphical symbol used in base 10 before switching to higher power (or higher weight rank).
Similarly, in base 2, the graphic 1 is the last symbol used before moving to the rank of higher weight.
To summarize, the complement to 1 of a binary number is the numerical value that must be added to this number to obtain the numeric value immediately below that of the higher power.
Example :
Or to find the complement to 1
of 1010.
the power immediately above
1010
is : 10 000. the next lower numerical value is :
1111 (see Figure 7). Let's put the operation : The binary number 0101 is the complement to 1 of 1010. If we add these two numbers, we obtain : 1111.
It should be noted that it suffices to replace the 0 with 1 and vice versa to find the complement to 1 of a binary number, the procedure is therefore very simple.
4. 3. 4. - COMPLEMENT A 2
(Return)
This is the binary equivalent of the 10 decimal complement, which we already know.
Since this is the numeric value that must be added to a given number to obtain the value of the power immediately higher, it can be obtained by taking the complement to 1 and adding 1.
Example :
Let's find the complement to 2 of 1010 :
It can also be found by subtracting the number 1010 from the numerical value corresponding to the next higher power :
In digital systems, the previous way is used because it is easier to obtain.
This supplement is called : Complement true.
A quick way to find the complement to 2 of a binary number, is to enumerate this number from the right (the lowest weight) and all 0 encountered until the first 1 are transcribed as well as this first 1, without change, then, systematically, we reverse all the symbols This complement will be used to carry out operations in digital systems.
In the explanations concerning the binary additions to 1 and 2, we had to perform some binary operations without you being informed of the rules that govern them.
These rules are the subject of this chapter and always for the sake of a better approach, we will describe these operations in decimal system, then in binary system.
Before dealing with these operations, it is necessary to recall the rules followed by the signs assigned to operations and numerical values of numbers.
The basic operations that one is brought to implement in the digital systems are :
When writing these numbers-based operations, they must be distinguished from each other by conventional symbols which are :
the sum or addition :
+ the difference or subtraction :
- the product or multiplication :
X the quotient or division :
/ the power rise :
Nn the extraction of the root : The signs of the sum and product operators should not be confused with those used frequently for the logical operations corresponding to the union and the intersection (the following symbols are preferably used for logical operations : Relative numbers are represented by an absolute numeric value associated with a positive (+) or negative (-) sign depending on whether they are larger or less than zero.
This relative sign, related to this absolute value, not to be confused with the sign of the operator, is placed, as well as the absolute value, between two parentheses.
The sign of the operator, placed in front of these parentheses, can, according to the operation, modify the relative sign attributed to the absolute numerical value, in the following way :
Example :
Example :
(+ 70) - (+ 30) = 70 - 30 = 40
[or ; (+ 40)] (+ 70) - (- 30) = 70 + 30 = 100
[or ; (+ 100)] Example :
(+ 5) x (+ 5) = (+ 25) (- 5) x (- 5) = (+ 25) Example :
(+ 12) x (- 3) = (- 36) Example : (+ 12) / (+ 3) = (+ 4) (- 12) / ( - 3) = (+ 4) The quotient can also be noted as follows :
Single-line writing with the slanted bar, the quotient symbol, is a more convenient notation from a typing point of view.
Example :
(+ 12) / (- 3) = (- 4) (- 12) / (+ 3) = (- 4) As a general rule, for the addition or for the subtraction, the first term is entered, then below, the following term or terms, by placing in the same columns the digits assigned to identical weights.
For the addition, more than two terms can be arranged one below the other.
We will then add the digits of the rightmost column (lowest weight).
In the decimal system, any result greater than 9 generates a carry in the next column of immediately higher weight.
Then add the numbers aligned in the second column, plus the report if it exists and so on until the last column occupied.
Position the highest column of the last column if there is one.
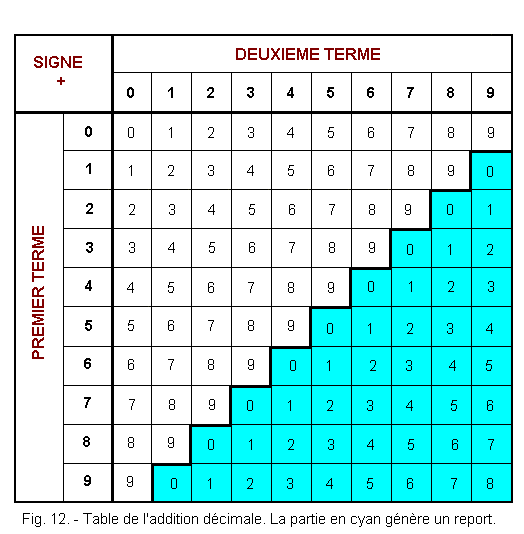
Figure 12 shows the table of the decimal addition. The first term is designated (to the left of the lines and in bold type), then the second term (in bold, upper column). The result is given in the box at the intersection of the row and the column corresponding to the chosen terms. in the cyan part, the sum of the terms 1 and 2 imposes a carry over in the column of higher weight.
The result of this operation is a total.
Example : Or to add 75 and 46 : Figure 13 gives the procedure.
The sum or addition is not limited to positive numbers, as we saw at the beginning of this chapter, but to the set of relative numbers.
In a general way, it gives the result of the sum of absolute values when the numbers are of the same sign and the difference if they are of opposite signs.
The sign of the result is the same as that of the two numbers which has the greatest absolute value.
Example :
(+ 75) + (+ 46) = (+ 121) (+ 75) + (- 46) = (- 29) (- 70) + (- 30) = (- 100) It is done in the same way as the decimal addition.
Since the count is based on 2, any result greater than 1 generates a carry over to the next column.
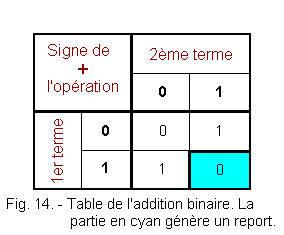
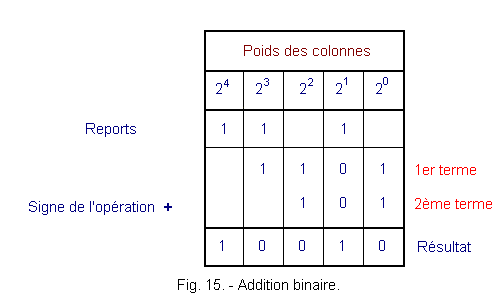
Figure 14 shows the table of the binary addition. The use of this table is carried out in the same way as for that of the decimal addition of Figure 12. In the cyan part, the sum of the terms 1 and 2 generates a carry. Note the great simplicity of this table compared to that of the decimal addition.
Example : Or to add 1310
and 510.
Let's transform each number into binary.
Figure 15 shows the process of adding these two binary numbers.
We obtain : 100102
The same sign rules also apply in the case of binary operations.
As with any operation, it will be necessary to proceed with order.
The first term is placed, and then the second term is aligned, making the identical weights coincide in the columns.
We start the subtraction by the rightmost column (of the lowest weight) by taking as a result the complement of the subtracted figure.
The subtracted figure is the one that is part of the subtracted number ; the latter corresponds to the first term.
The subtractor is the number that is part of the subtractor number ; the latter corresponds to the second term.
If the digit subtracted from a numeric value lower than that of the subtractor, a loan is generated in the next higher weight column, which is carried forward as a hold in this same column, subtracting this deduction from the subtracted figure.
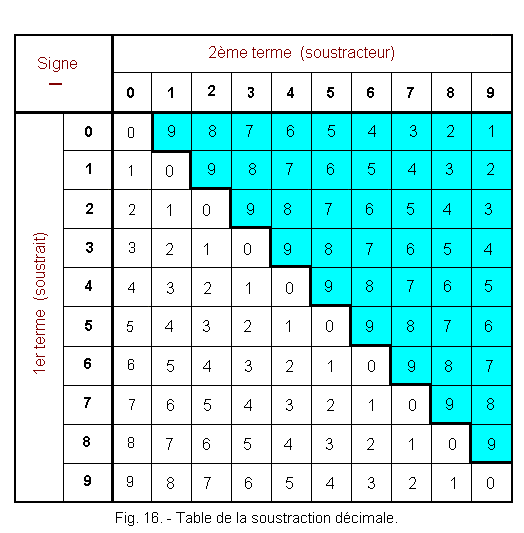
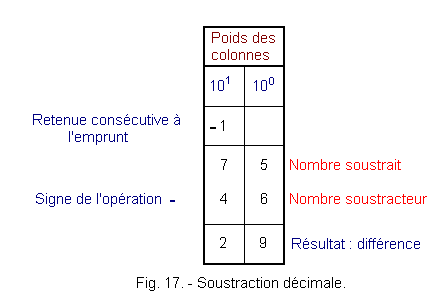
Figure 16 shows the decimal subtraction table. In the cyan part, the subtracted term has a lower numeric value than the subtractor term, the operation generates a loan in the higher weight column. The result of this operation is a difference.
Example : Either to subtract
46 of 75.
Figure 17 shows the process of this subtraction in decimal.
Beginning with the lowest column of weight, we see in this example that we can not reduce a larger number by a smaller number. We will have to practice a loan in the next higher column.
Thus, we can realize the subtraction, the subtracted number is no longer 5, but : 10 + 5 is 15, to which we can subtract 6. The difference is 9.
This borrowing of a unit in the tens column, we must now subtract it in this same column, otherwise the number subtracted (75) would see its numerical value modified (it would become equal to 85).
Once this deduction has been made, the subtraction can continue to the last column occupied.
The result or difference, is the complement of the subtractor number with respect to the subtracted number.
If we add the result and the subtractor number, we find the number subtracted.
In the case where the number subtracted has a numerical value greater than or equal to the subtractor number, the operation is possible and the result is positive or zero.
In the case where the number subtracted has a lower numerical value, to perform the operation, a device is used. There are several, the simplest is to reverse the terms :
the subtracted number becomes subtractor the subtractor becomes the subtracted number. When doing this inversion, the negative value (-) is assigned to the numerical value of the result.
This is a quick and convenient method, because you can also use the loan in the next higher column. In this case, we obtain the complement to 100 of the result.
One can also proceed by adding the complement of the subtractor number to the subtracted number as we will see in the chapter on operations in digital machines (the term machine is used here to denote a system working with digital signals).
In general, decimal or binary operations follow the same rules.
In the lowest weight column, we subtract the subtractor from the subtracted figure, that is, we take the complement of the subtracter in relation to the subtracted figure.
If the digit subtracted from a numeric value lower than that of the subtractor, borrowing from the subtracted subtraction of the next higher weight column.
This is done from a columnar column to the last one representing the highest weight.
As with decimal subtraction, if the term subtracts from a smaller numerical value than the term subtractor, the operators are reversed and the (-) sign is assigned to the result.
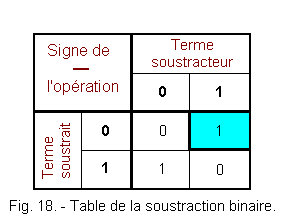
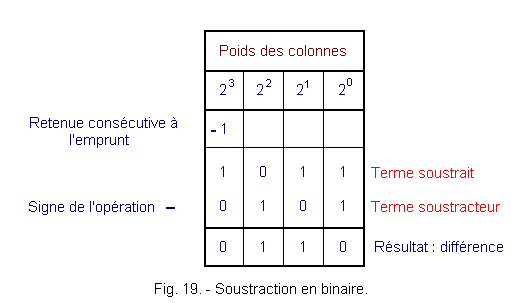
Figure 18 represents the binary subtraction table, the cyan box corresponds to a borrowing at the subtracted term from the next higher weight column.
Again, there is a great simplicity in this table compared to that of the decimal subtraction.
Example : Either to subtract
510
of 1110.
Let's make the transformation into binary :
1110 → 510
→ 1012 Figure 19 shows the progress of the binary subtraction.
The result is :
1011 - 101 = 110 Either in decimal :
1102 The loan generated by the transaction in column 22
is carried forward as a holdback to the next higher weight column (either 23).
The same remarks as for decimal subtraction can also apply in this case.
Multiplication is a series of additions. For example, if you want to multiply 15 x 5,
simply add five times the number 15 with itself to get the result.
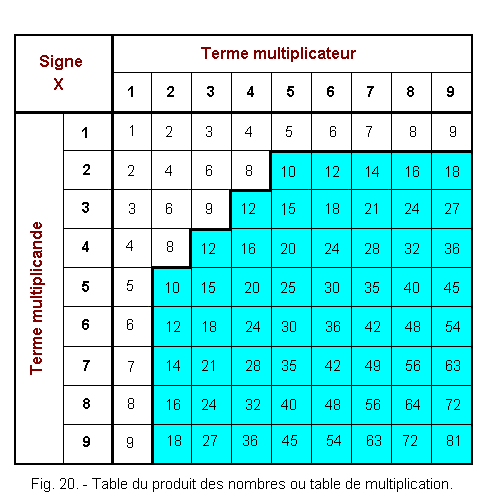
Multiplication tables are made to avoid these additions.
The number that represents the quantity that must be multiplied is called the multiplicand.
The second term of the product is called the multiplier.
Thus, in the previous example, 15 is the multiplicand and 5 is the multiplier.
Figure 20 shows the multiplication table.
The result is read in the box corresponding to the intersection of the multiplicand line with the multiplier column.
The cyan part generates a report that will have to be added to the next product.
To perform this operation, the product of the digit occupying the lowest rank of the multiplier is calculated with each digit assigned to the different weights of the multiplicand, starting with the lowest weight.
When one of these products generates a report, it will be added to the next product.
When these products are made, they constitute the first partial result.
The second partial result is obtained by making the product of the second digit of the multiplier with each multiplicand digit as before.
This second partial result will be positioned under the first and shifted one rank to the higher weights, since it is a product obtained with the multiplier figure occupying the weight rank 101.
If there are, the other partial results will be arranged under the previous ones, respecting the offset due to the rank of the multiplier figure.
The final result will be expressed as the sum of the partial results.
It should be noted that there are as many partial results as there are numbers to the multiplier.
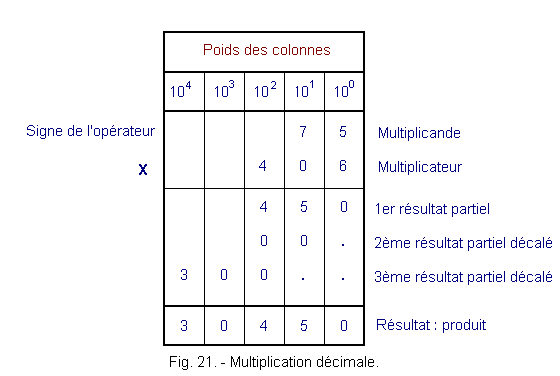
Example : Either multiply 75 by 406.
Figure 21 describes this multiplication.
The product of 0 by a number N is equal to
0. The product of a number N
by 0 does not make sense, but if we apply commutativity, we go back to the previous case and the result is equal to 0. The sign of the product is determined by the rules at the beginning of this chapter because the product applies to relative numbers (not just positive numbers as in our example). We recall below these rules, which also apply to binary operations :
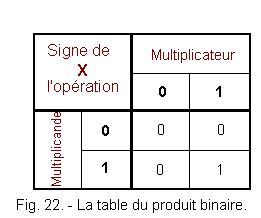
a positive number multiplied by a positive number gives a positive product. a negative number multiplied by a negative number gives a positive product a negative number multiplied by a positive number gives a negative product (the opposite gives the same result when the sign). The binary system, based on two elements, results in a simplification of the calculation. This simplification is even more sensitive with multiplication. Indeed, this operation does not generate any transfer or loan. Figure 22 shows the binary multiplication table.
As for the 10-based system, the multiplication by 0 causes a result equal to 0. The multiplication by 1 causes the copying of the multiplicand.
The procedure for obtaining the result is identical to that of the decimal multiplication (or for any other multiplication in another numbering system).
Example : Either multiply
1110
by 2010.
Let's turn its two numbers into binary.
1110 → 2010
→ 101002 Figure 23 shows this binary multiplication. The result of this product is therefore 110111002,
which is equivalent to the decimal number 22010.
The quotient, which is the inverse operation of the product, is therefore a sequence of differences or subtractions (the product being a continuation of addition).
The sign rules at the beginning of the chapter apply to the decimal or binary quotient.
The quotient is composed of a number to divide, which is called the dividend, of a divisor number, which one names divisor.
The number of times we can subtract the divisor from the dividend, until this is no longer possible, gives us the quotient.
If the last subtraction indicates a null result, the quotient is called integer (or exact).
If, on the contrary, there is a remainder, the quotient is said to be approximate.
Example : Either divide 75
by 15.
Figure 24 outlines a possible method.
We can subtract the number 15 from the number 75 five times, so the quotient is 5 and since the last result is zero, the quotient is integer.
The multiplication of the quotient by the divisor, added to the rest if it exists, restores the dividend.
The procedure for obtaining the result, in practice, does not take place according to this method of successive subtractions which is too long. As a result, this operation is a little more delicate than the others.
We begin by looking for how many times the divisor is contained entirely in the number constituted by the digit or numbers occupying the highest ranks of the dividend.
This number constitutes the first partial dividend. The number of times the divisor is contained in this first partial divisor is the first digit assigned to the highest weight of the
du quotient.
Subsequently, the product of the divisor is subtracted by this partial quotient, the first partial dividend, and this difference (larger or equal to zero) constitutes, with the figure occupying the next weight of the dividend, the second partial dividend.
Once again, we look for how many times the divisor is contained in this second partial dividend and the product of the divisor by the second quotient is subtracted from it.
These operations are carried out until the dividend no longer has a significant number, if the last difference is equal to zero, the quotient is said to be exact (the dividend is an integer multiple of the divisor).
If it is not so, the quotient is said to be approached
and the division comprises a remainder.
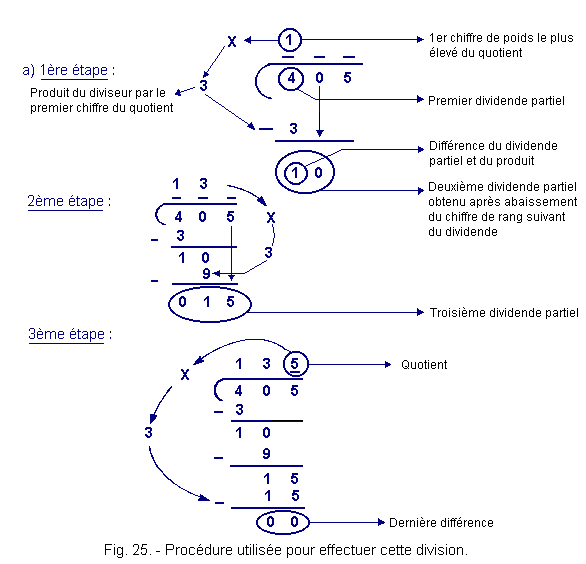
Example : Let divide 405 by 3.
For convenience, the operation can be arranged as follows :
Figure 25 gives the procedure adopted to perform this division.
We are in the presence of an exact quotient (135), the last difference being equal to zero. The number 405 is a multiple of 3.
This procedure involves two operations :
the multiplication the subtraction. These operations are described in Chapters 5.5 and 5.3 and the corresponding tables.
These operations are easier to perform than to enumerate, because we acquired automatisms.
There is no question of calling into question these automatisms, but they sometimes forget the basic processes that we use for frequent tasks.
Reminding them, the similarity between decimal and binary operations appears better and the procedures used in digital machines will seem more familiar to you.
The path to obtain the result is identical to that of the decimal division. Therefore, we will move to an example.
The practical procedure involves two operations :
multiplication or product subtraction or difference. These operations are familiar to us, their tables are shown in Figure 22 and Figure 18.
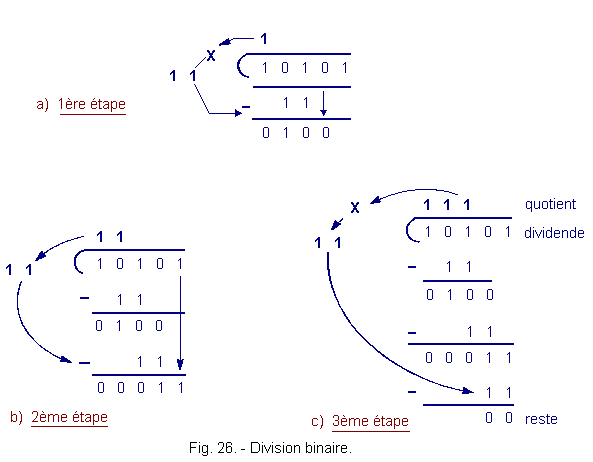
Either to divide 101012 (2110)
by 112 (310).
Figure 26 shows the procedure used which is quite similar to the method used in decimal.
The division stops there, because the rest is equal to zero and there is no more digit, the dividend, to combine with the rest.
The result of the division is therefore 1112
whether 710.
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.
the absolute value of a number is the value assigned to it by the numbering system adopted without regard to its sign. This value is represented between 2 vertical dashes :
4. 3. - COMPLEMENT OF A NUMBER
Le complément à 9 du nombre 128 est :
103 or 1000
The subtraction of the two terms (999 and 128) does not result in any borrowing, or retention, in the higher weight column.
the next highest power is : 1000 (103).
the 1000 complement of
128 is : 1000 - 128 = 872.
.gif)
5. - REMINDER
ON BASIC OPERATIONS
the sum, or addition,
and the inverse operation which is the difference or subtraction.
the product, or multiplication,
and the inverse operation which is the quotient or division.
the rise to a power nième
and its inverse operation, the extraction of the nth root.
for the union and 
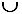for the intersection).
If the parentheses are preceded by the sign of the sum (+ : plus), the sign of the absolute value contained between these parentheses is not modified.
If the parentheses are preceded by the sign of the difference (- ; minus), the sign of the absolute value between these parentheses must be changed.
In the case of the product of two relative numbers, the absolute value of the result is positive (+) if the two numbers are of the same sign.
The absolute value of the product of two relative numbers is negative, if these two numbers are of opposite signs.
The absolute value of the quotient of two relative numbers is positive, if the two numbers are of the same signs.
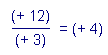
The absolute value of the quotient of two relative numbers is negative, if these two numbers are of opposite signs.
5. 1. - DECIMAL ADDITION
.gif)
5. 2. - BINARY ADDITION
(Return)
5. 3. - DECIMAL SUBTRACTION
OR DIFFERENCE
5. 4. - BINARY SUBTRACTION
10112
→
610
5. 5. - THE PRODUCT OR DECIMAL
MULTIPLICATION
5. 6. - THE
BINARY PRODUCT
(Return)
10112
5. 7. - DIVISION OR QUOTIENT DECIMAL
5. 8. - THE BINARY QUOTIENT
Click here for the next lesson or in the summary provided for this purpose.
Top of page
Previous Page
Next Page
Nombre de pages vues, à partir de cette date : le 27 Décembre 2019
