NOTA :
Le but d’électronique est de vous expliquer certaines règles qui peuvent vous aider dans certains domaines et notamment sur les fonctionnement des ordinateurs. Nous commencerons sur des pages différentes. « Electronique » qui vous permettra de naviguer afin de vous guider et, à suivre les leçons dans l’ordre correspondantes. Donc, Nous commencerons par la loi d’Ohm puis la loi de Joule et bien d’autres. Certains paragraphes sont destinés aux débutants.
Nous vous conseillons également de commencer les leçons d’électroniques fondamentales qui a pour but de bien comprendre l’ensemble des programmes en commençant par la loi d’Ohm et en suivant les leçons dans l’ordre. Ensuite, testez vos connaissances prévues à cet effet afin que vous puissiez vous rendre compte de l’exactitude des leçons que vous aviez appris antérieurement. Vous pouvez choisir les leçons de votre choix par exemple l’électronique digitale ainsi que la pratique correspondante, (14 leçons et 14 pratiques digitales). Pour bien faire, vous devez commencer la 1ère leçon théorique digitale puis la 1ère leçon pratique digitale, ensuite, la 2ème leçon théorique et la 2ème leçon de pratique et ainsi de suite pour en profiter pleinement de l’éducation de ce site.
1. – NOTION DE RÉSISTANCE ÉLECTRIQUE
Tout courant électrique dans un conducteur est dû à un déplacement d’électrons. Durant leur déplacement, ces électrons rencontrent des obstacles dû aux atomes du conducteur.
Un conducteur présente une certaine opposition au passage du courant électrique, opposition qui est appelée résistance électrique.
La notion de résistance électrique peut s’étendre à n’importe quel matériau, même aux isolants dans la mesure où ceux-ci opposent au déplacement des charges électriques une résistance tellement grande qu’elle empêche quasiment tout passage de courant.
La résistance se classe parmi les grandeurs électriques et possède son unité.
1. 1. UNITÉ DE MESURE DE LA RÉSISTANCE ÉLECTRIQUE
La résistance électrique (symbole R) se mesure en Ohm (symbole Ω).
Ω est la dernière lettre de l’alphabet Grec : Oméga. Pour indiquer la valeur des résistances, on utilise fréquemment des multiples de l’Ohm tel que le kiloohm (symbole kΩ) qui vaut 1000 Ohms ou le mégohm (symbole MΩ) qui vaut 1 million d’Ohms.
La résistance R d’un conducteur électrique est définie par trois paramètres :
sa longueur
sa section
sa nature
1. 1. 1. – INFLUENCE DE SA LONGUEUR
Il est évident que la résistance rencontrée par les charges électriques se déplaçant dans un conducteur est d’autant plus grande que ce conducteur est long, car le nombre des atomes rencontrés par les charges sur leur chemin est plus important.
La résistance d’un conducteur est donc proportionnelle à sa longueur.
1. 1. 2. – INFLUENCE DE SA SECTION
Les charges électriques se meuvent d’autant plus facilement que la section du conducteur est importante. Pour imaginer cela, on peut dire que les charges électriques ont un espace plus important pour se déplacer.
La résistance d’un conducteur est donc inversement proportionnelle à sa section.
1. 1. 3. – INFLUENCE DE SA NATURE ET NOTION DE RÉSISTIVITÉ
Deux conducteurs de même longueur et de même section, mais de nature différente, c’est-à-dire constitués de matériaux différents (par exemple l’un en cuivre, l’autre en fer) présentent des résistances électriques différentes.
La différence entre les propriétés électriques des matériaux est caractérisée par leur résistivité. Le symbole de la résistivité est la lettre grecque r (rhô) et son unité est l’ohm-mètre (Ω-m). Figure 1-a sont regroupées les résistivités des principaux métaux purs et des alliages d’usage courant en technique électrique.
| Métal | Résistivité à 20°C |
| Argent | 1,6 x 10-8 Ω-m |
| Cuivre | 1,7 x 10-8 Ω-m |
| Aluminium | 2,8 x 10-8 W-m |
| Tungstène | 5,6 x 10-8 Ω-m |
| Fer | 9,6 x 10-8 Ω-m |
| Platine | 10 x 10-8 Ω-m |
| Plomb | 22 x 10-8 Ω-m |
| Mercure | 95 x 10-8 Ω-m |
Un petit commentaire sur ces tableaux est nécessaire, on s’aperçoit que la résistivité n’est pas exprimée en Ω-m et ceci parce que cette unité est beaucoup trop grande pour les conducteurs. Dans la figure 1-a, on utilise le cent millionième d’ohm-mètre (10-8 Ω-m). Mais suivant les ouvrages, vous pouvez trouver cette résistivité exprimée en µΩ-m (micro ohm-mètre) qui vaut 10-6 Ω-m ou encore en µΩ-mm. Inversement pour les isolants dont la résistivité est importante on utilise le mégohmmètre (MΩ-m) qui vaut 106 (1 million) Ω-m.
1. 1. 4. – DÉTERMINATION DE LA RÉSISTANCE ÉLECTRIQUE D’UN CONDUCTEUR
Comme nous venons de le voir, la résistance électrique d’un conducteur est définie par trois paramètres. Nous pouvons donc penser que ces paramètres peuvent être liés entre eux par une relation permettant de déterminer la résistance d’un conducteur donné connaissant ses dimensions et sa nature.
Nous savons déjà que cette résistance est proportionnelle à la longueur :
R = f (l) (se lit R en fonction de l).
Nous savons également que cette résistance est inversement proportionnelle à la section :
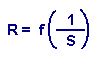
La résistivité du conducteur intervient également dans ce calcul. L’unité de résistivité étant l’ohm-mètre ; ainsi, plus le conducteur sera long plus l’influence de sa résistivité se fera sentir sur le déplacement des électrons donc sur la résistance de conduction :
R = f (r)
De la combinaison des trois relations précédentes, nous pouvons déduire la formule générale pour déterminer la résistance d’un conducteur :

Connaissant cette formule, nous pouvons à titre d’exemple calculer la résistance que présente un conducteur en cuivre de 100 m de longueur et de 1 mm² (10-6m²) de section, sachant que la résistivité du cuivre est 1,7 x 10-8 Ω-m.
.gif)
Pour compléter notre exemple, la figure 1-c donne la résistance de conducteurs de 100 m de long et de 1 mm² de section mais réalisés en différents matériaux, et ce dans le but de réaliser une meilleure analyse comparative de ces métaux au point du vue électrique.
| Métal | Résistance d’un fil de 100 m de long et de 1 mm² de section |
| Argent | 1,6 Ω |
| Cuivre | 1,7 Ω |
| Aluminium | 2,8 Ω |
| Tungstène | 5,6 Ω |
| Fer | 9,6 Ω |
| Platine | 10 Ω |
| Plomb | 22 Ω |
| Mercure | 95 Ω |
Enfin, pour clore ce chapitre sur la résistance électrique, il faut savoir que celle-ci varie avec la température car la résistivité de la substance varie avec la température également. Toutefois, toutes les substances ne réagissent pas de façon identique. En règle générale, la résistivité augmente lorsque la température augmente mais dans des proportions différentes suivant les substances.
Les alliages, bien que possédant une résistivité plus importante que les métaux purs (figure 1-b), ont par contre une résistivité beaucoup plus stable.
Par exemple la manganine et le constantan (ce qui justifie le nom donné à cet alliage) sont particulièrement utilisés pour la réalisation des résistances étalonnées ou des ohms-étalons (résistances spécialement construites pour représenter aussi exactement que possible l’unité de résistance électrique).
Quelques substances voient, par contre, leur résistivité diminuer lorsque la température augmente et c’est notamment le cas de certains mélanges d’oxydes ou de sulfures.
1. 2. – CONDUCTANCE ET CONDUCTIVITÉ
Jusqu’à présent, nous avons considéré les conducteurs du point de vue de la résistance qu’ils opposent au passage du courant, mais comme son nom l’indique, ce conducteur sert à acheminer le courant d’un point à un autre.
L’aptitude d’un conducteur à acheminer plus ou moins bien le courant s’appelle la conductance électrique. Un conducteur présente une conductance d’autant plus grande que sa résistance est faible. La conductance sera donc l’inverse de la résistance.
Le symbole de la conductance est G et son unité est le Siemens (symbole S).
Comme nous avons défini une résistivité, nous pouvons définir une conductivité qui est l’inverse de la résistivité.
G = 1 / R
Le symbole de la conductivité est g (se lit gamma, lettre de l’alphabet grec) et son unité est le Siemens / mètre (symbole S / m).
Comme nous l’avons vu, nous pouvons appeler conducteurs tous les éléments qui présentent la propriété de se laisser facilement traverser par le courant, ils ont donc une conductivité élevée et offrent une faible résistance à ce courant : c’est notamment le cas des fils de cuivre utilisés pour effectuer les liaisons dans les circuits électriques.
Dans ces circuits cependant, il se présente souvent la nécessité d’opposer au courant une résistance plus ou moins élevée, ceci s’obtient par l’emploi d’éléments réalisés à partir de matériaux à haute résistivité.
Ces éléments ne peuvent plus être considérés comme des conducteurs à part entière dans la mesure où leur rôle spécifique est d’opposer au courant électrique une résistance déterminée.
Pour cette raison, ces éléments sont appelés des résistances et caractérisés par la résistance, exprimée en ohm, qu’ils opposent au courant.
Dans le tableau de la figure 1-d sont regroupées les quatre grandeurs que nous venons d’examiner. Pour chacune d’elles sont reportés l’unité, le symbole correspondant et les relations existant entre ces grandeurs.
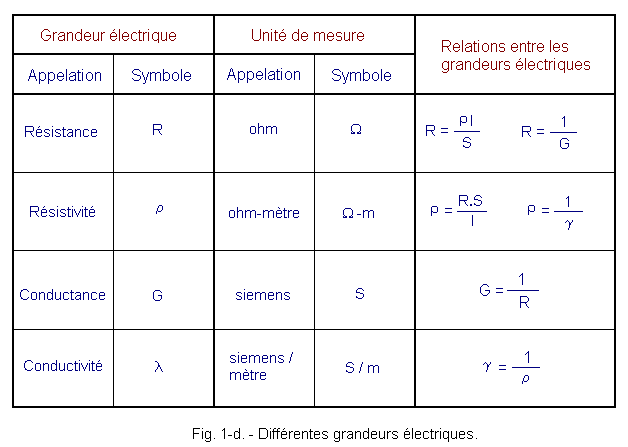
La plus importante de ces grandeurs est sans conteste la résistance car nous pouvons directement mesurer sa valeur par comparaison avec des éléments connus, comme nous le verrons en temps utile.
2. – LA LOI D’OHM
Toutes les grandeurs électriques relatives à un circuit sont maintenant définies. Nous connaissons la tension, le courant (ou intensité) et la résistance. Nous pouvons passer à l’examen d’un circuit complet et voir quelle influence ont chacune de ces trois grandeurs sur son fonctionnement. Commençons par le circuit très simple tel qu’il est représenté figure 1-a).
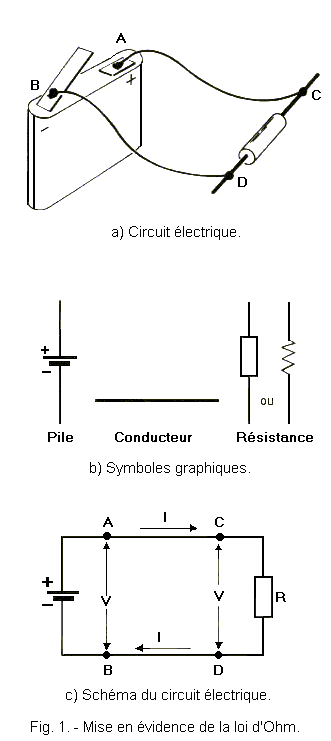
Ce circuit est constitué d’une résistance reliée à une pile, l’insertion de la résistance est nécessaire pour que le circuit présente une valeur résistive bien déterminée.
Figure 1-a, les composants du circuit sont représentés sous leur aspect réel mais lors de l’examen des circuits électriques on considère toujours les composants sous leur aspect symbolique. Nous obtenons ainsi le schéma électrique du circuit à analyser.
Figure 1-b sont donnés les symboles électriques des trois composants de notre circuit, tandis que la figure 1-c apparaît son schéma électrique
Les lettres A, B, C et D des figures 1-a et 1-c désignent les points où les deux conducteurs reliant la pile et la résistance sont soudés sur ces deux éléments. La partie du schéma à gauche des points A et B représente le circuit interne de la pile tandis que la partie à droite de ces mêmes points représente le circuit extérieur à la pile, circuit constitué par les conducteurs et la résistance.
Sur la figure 1-c, nous pouvons indiquer clairement les différentes grandeurs électriques connues.
La tension obtenue aux bornes de la pile entre les points A et B est désignée par son symbole V. Ce symbole est inscrit entre les deux flèches qui mettent en évidence les point A et B, points entre lesquels apparaît cette tension.
La même tension V est également présente aux bornes de la résistance R, c’est-à-dire entre les point C et D, car le point (C) est relié directement au point (A) et donc possède le même potentiel électrique que ce point ; il en est de même avec le point D relié directement à B.
La résistance du circuit extérieur à la pile est repérée par son symbole R. On ne tient compte que de la valeur résistive de la résistance et l’on néglige celles des conducteurs et de la pile qui sont très faibles. Enfin, le courant qui traverse le circuit est désigné par son symbole (I) avec la flèche montrant la direction de son déplacement suivant le sens conventionnel. Nous voyons clairement sur ce schéma que le courant part du pôle positif de la pile, traverse le conducteur AC puis la résistance R et revient au pôle négatif de la pile via le conducteur DB.
La tension V existante aux bornes de la pile a tendance à provoquer la circulation du courant I tandis que la résistance R présente un obstacle à son passage : on comprend que l’intensité va dépendre de la tension et de la résistance. En d’autres termes, il doit exister une relation qui lie entre elles ces trois grandeurs électriques fondamentales.
Cette relation fut découverte par le physicien Allemand Georges Simon OHM (1789-1854) et fut appelée loi d’Ohm. L’unité de résistance porte également le nom de ce physicien.
Ohm put énoncer sa loi à la suite de nombreuses expériences et de mesures minutieuses ; pour se faire une idée du procédé qu’il adopta, on peut faire quelques remarques simples.
Comme la tension de la pile est la cause qui détermine la circulation du courant dans le circuit, si on augmente la tension, on augmente aussi l’intensité du courant ; on peut facilement vérifier ce fait en reliant successivement au circuit des piles qui donnent des tensions toujours plus élevées et en mesurant l’intensité du courant que chacune d’elles fait circuler, mais on peut aller plus loin.
En effet, si on divise la tension de chaque pile par l’intensité du courant qu’elle fait circuler, on trouve toujours la même valeur ; cette valeur ne varie donc pas, bien qu’on fasse varier la tension, et aussi par conséquent l’intensité du courant.