 KARNAUGH's method KARNAUGH's method |
 Footer Footer |
Monome - Polynomial - Karnaugh Method - Graphical Simplification :
3. - N VARIABLE FUNCTIONS
3. 1. - FUNCTIONS OF A VARIABLE
Given that a variable a can only take two values 1 or 0, we can imagine functions f0 (a), f1 (a), f2 (a) representing all the possible combinations obtained with these two values.
We see in the table (Figure 51) that there can exist for a variable 4 distinct functions.

We have two constant functions :
f0 = 0 whatever is a
f3 = 1 whatever is a
![]() A function YES : f1 = a
A function YES : f1 = a
![]() A function NO : f2 =
A function NO : f2 = ![]()
3. 2. - FUNCTIONS OF 2 VARIABLES
The number of functions for two variables is 16 (Figure 52).
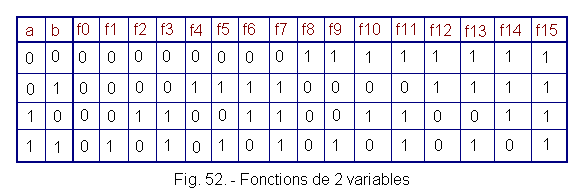
There are a number of remarkable features :
f0 = 0 some are a et b "constant function"
f15 = 1 some are a and b "constant function"
f3 = a
f5 = b
f12 = ![]() function NO
function NO
f10 = ![]() function NO
function NO
f1 = ab function AND
f7 = a + b OR INCLUSIVE function

We call f14![]() or
NAND (of the English NO AND which means NON ET).
or
NAND (of the English NO AND which means NON ET).
One calls f8 ![]() or
NOR (of the English NO OR which means NON OU).
or
NOR (of the English NO OR which means NON OU).
We call f6 OR EXCLUSIVE that we also note :
f6 = a Å b
We call f9 logical identity that we also notet :
a ≡
b
or f9 = a ![]() b
b
We also note the functions :
f2 = a![]()
f4 = ![]() b
b
f11 = a + ![]()
f13 = ![]() + b
+ b
3. 3. - ALGEBRIC SIMPLIFICATIONS
3. 3. 1. - MONOME
We have seen for two variables a number of algebraic expressions.
Take the function f9 = ab + ![]()
![]() .
We will say that the algebraic expression ab +
.
We will say that the algebraic expression ab + ![]()
![]() is a polynomial composed of a monome ab and a monomial
is a polynomial composed of a monome ab and a monomial ![]()
![]() .
.
In Boolean algebra, a monomial is an algebraic expression consisting of the product of several variables among them, such as abc, ab![]() ... etc. It should be noted that in Boole algebra
x .
x = x, there are no exponents such as x2,
x4, this does not exist.
... etc. It should be noted that in Boole algebra
x .
x = x, there are no exponents such as x2,
x4, this does not exist.
3. 3. 2. - POLYNOMY
A polynomial will be a sum of monomials or sum of products.
3. 3. 3. - ADJACENT MONOME
Adjoining monomials are monomes that differ from one another only by a single variable. In a sum of two adjacent monomials, the variable that differs is eliminated.
Example :
![]()
3. 3. 4. - ALGERY REDUCTION
A simple method of algebraic reduction is to look for the adjacent monomials after having put the algebraic expression which one seeks to simplify in the form of a sum of products or polynomials which one calls canonical form. Then, it will suffice to look for simplifications in the same way as we did for the absorption property and by using the remarkable identities in order to bring out simplifications.
Example N° 1 :
![]()
We can write :
Since we know that we can add xyz already present as many times as we want without changing the value of f.
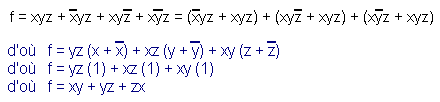
Example N° 2 :
![]()
Multiply member to member expression :
![]()
Multiply again member to member expression :
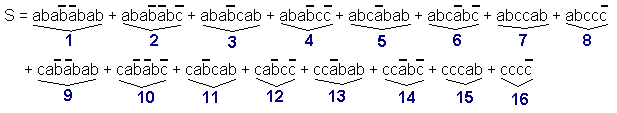
which becomes by removing the useless terms :

![]() 3. 4. - KARNAUGH
METHOD
(Back to theory 3)
3. 4. - KARNAUGH
METHOD
(Back to theory 3)
The algebraic simplification of Boolean equations is not always obvious and requires intuition. Conversely, Karnaugh's method makes it possible to highlight the adjacent monomials using a table without difficulty.
This method works very well from 2 to 5 variables, it becomes complex beyond.
3. 4. 1. - TABLES OF KARNAUGH
a) - The painting
Karnaugh's painting is a particular form of the truth table we have used so far (truth table Figure 53) :
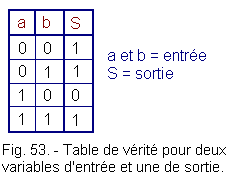
A truth table has as many columns as there are input variables. It includes one or more other columns, those of the output variables. Any combination of values that input variables can take is searched by counting in a binary order. The value of the output variables is indicated opposite the corresponding combination.
The table of Karnaugh includes him 2n boxes, n being the number of variables of entries of the function considered.
b) - Case of two variables
In this case, the number of boxes is 2n = 22 = 4 (Figure 54).
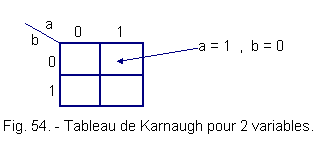
The order of the variables in abscissa or ordinate does not matter, only it is very important the fact that when we go from one box to the adjacent box, only one variable changes.
Example :
Let us represent the function f = a . b "function AND" (Figure 55).
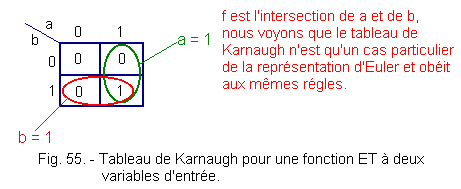
We can easily see that we have put the binary value that can take the output inside the box for which the variables have the value carried in abscissa and ordinate.
f is 1 only for a = 1 and b = 1
c) - Case of three variables (Figure 56).
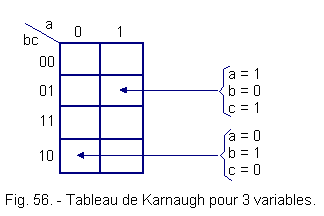
Whereas for two variables the table was square, it is now rectangular ; indeed, we have represented the variables bc on the same column.
We can notice that the order of the fourth and third lines seems reversed. In reality, it is not so. We only use the gray or binary code reflected in order to change only one variable at a time horizontally or vertically.
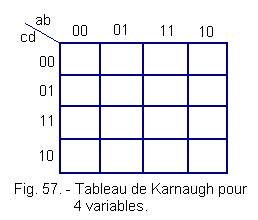
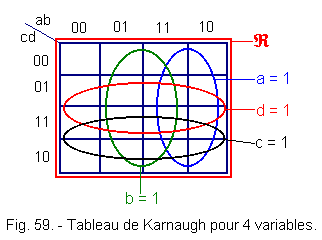
d) - Case of four variables (Figure 57)
We find a square that has 24 boxes :
24 = 16 boxes
We see again, which is absolutely essential, that with the Gray code, moving from one box to another horizontally or vertically only one variable changes.
3. 4. 2. - GRAPHIC SIMPLIFICATION
a) - We must now use Karnaugh's chart to search for adjacent monomials instead of looking for them algebraically.
The table of Veitch (Figure 58) includes on the abscissa and the ordinate the algebraic expressions represented for each box. For example : case a![]() c
c![]() .
.
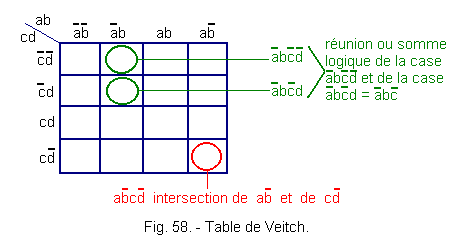
Karnaugh's table (Figure 59) gives, for each box, the values that the variables take in terms of abscissa and ordinate.
In both systems, we indicate inside each box the value 1 or 0 taken by the monomer considered.
It is easy to see that two adjacent monomials will be in two adjacent cells since it was originally said that Karnaugh's paintings were made in such a way that only one variable is changed when a box is changed.
It will therefore be sufficient for each combination of variables to note 1 or 0 in the corresponding box, according to the result found for the value of the function considered, then to group the adjacent boxes whose content is 1 per group of 2, 4 or 8 or 2n adjacent terms.
Example (Figure 60)
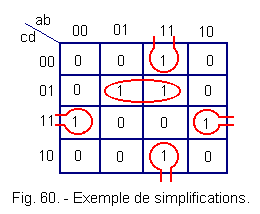
Groupings (here of 2 terms) are shown in red, note that the boxes ab![]()
![]() and abc
and abc![]() are the boxes representing adjacent monomials. One can compare the table represented on the surface of a torus if one tries to bring all the boxes of the monomials adjacent to each other ; thus, if the boxes of the four corners of the table were to 1, one could constitute a grouping of 4 boxes with them.
are the boxes representing adjacent monomials. One can compare the table represented on the surface of a torus if one tries to bring all the boxes of the monomials adjacent to each other ; thus, if the boxes of the four corners of the table were to 1, one could constitute a grouping of 4 boxes with them.
b) - Example for a table with 3 variables :
Let the expression : S = a![]() c
+ c
c
+ c![]() +
+ ![]() a
a![]() linking the variable S to the variables a, b, c.
linking the variable S to the variables a, b, c.
Let's establish the truth table (Figure 61) (Figure 61)
-
Simplification by algebra
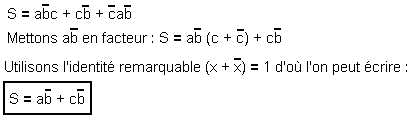
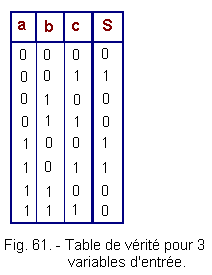
-
Simplification by Karnaugh's paintings
Let's show the values of S in the Karnaugh table (figure 62) :
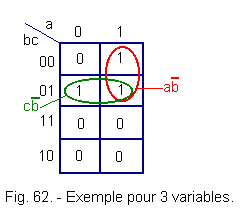
Let's realize the groups a![]() and c
and c![]() .
.
We can write :
S = a![]() + c
+ c![]()
c) - Example for a four-variable array :
Let : S = abcd + abd + bc link the variable SS to the variables a, b, c, d.
Let's establish the truth table (Figure 63) :

-
Algebraic simplification :
S = abcd + abd + bc
Let abd in factor :
S = abd (c + 1) + bc
Let's use remarkable identity (x + 1) = 1 from where (c + 1) = 1 from which one can write :
S = abd + bc
-
Simplification by Karnaugh's paintings
Let's put the value of S in the table (Figure 64).
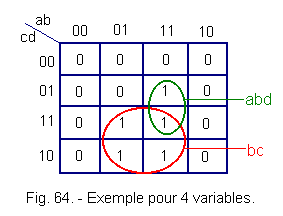
Let's realize the groups abd and bc.
We can write :
S = abd + bc
d) - Case of 5 variables
From five variables, the problem is complicated a little. Indeed, it is not possible to obtain on a flat surface a table in which one box is adjacent to 5 other boxes. However, it is possible to use Karnaugh's method by making two tables (Figure 65).
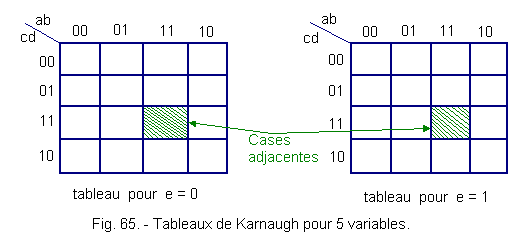
We see that by superimposing the two tables (Figure 66), we can obtain a given box X, five adjacent squares.
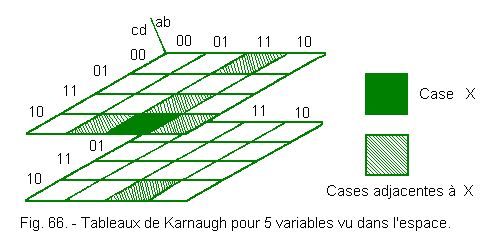
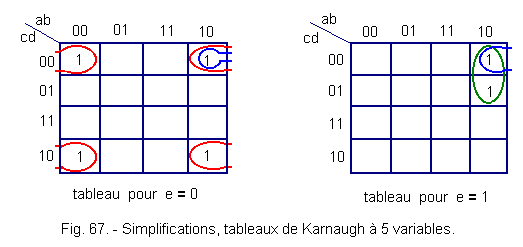
Figure 67 shows a case where three groups could be carried out :
![]() red Grouping : the four corners in the same plane (table for e = 0)
red Grouping : the four corners in the same plane (table for e = 0)
![]() Green grouping : two boxes in the same plane for e = 1
Green grouping : two boxes in the same plane for e = 1
![]() Blue grouping : two superimposed boxes.
Blue grouping : two superimposed boxes.
NOTE :
We see in this example that the blue group seems to be superfluous. It is necessary when one uses an electric or electronic technology for reasons of good operation that there is regrouping between the groups.
This condition is however not mandatory in the tire.
A grouping can only include 2n squares, that is, 1, 2, 4, 8, 16, 32, ... squares.
e) - Case of 6 variables
The same principle is used with four tables for six variables.
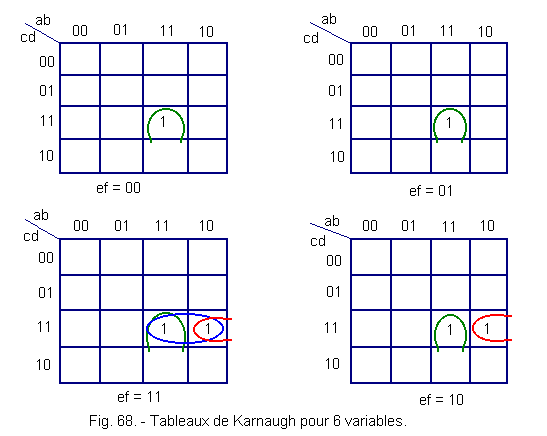
The example in Figure 68 shows three groupings :
![]() in green on four levels
in green on four levels
![]() in red on two levels
in red on two levels
![]() in blue in the same plane
in blue in the same plane
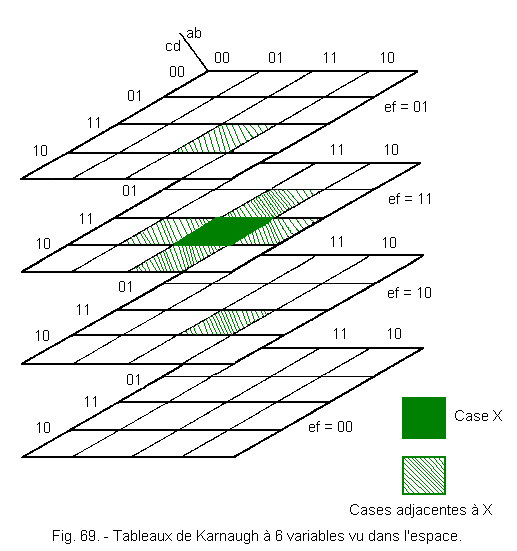
Figure 69 shows in space an example of adjacent squares.
Beyond 6 variables, Karnaugh's method is no longer valid, we use the so-called Mac Cluskey method that we will describe later so as not to confuse with that of Karnaugh.
We will continue to deepen this lesson with practical applications of Karnaugh's paintings on another page so as not to clutter this one.
 Click here for the next lesson or in the summary provided for this purpose. Click here for the next lesson or in the summary provided for this purpose. |
|
 Previous Page Previous Page |
 Next Page Next Page |
Nombre de pages vues, à partir de cette date : le 27 Décembre 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.
