Logical Product of Two Variables - Representation of Euler :
2. 8. - LOGICAL PRODUCT OF TWO VARIABLES
2. 8. 1. - EXAMPLE AND DEFINITION
Suppose now that we ask : Is Jacques at school ? YES or NO. There are two possible answers again.
But now, are Paul AND Jacques at school ?
Let's summarize the different answers on the chart (Figure 22).
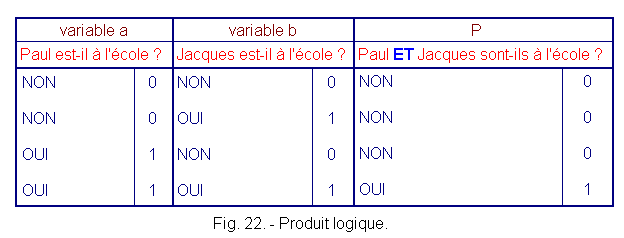
We see that when "Paul and Jacques are in school", we need "Jacques" is in school" AND "Paul is in school."
We have just defined the logical function AND.
We can write P = a . b that we will read P = a AND b.
2. 8. 2. - REPRESENTATION OF EULER OR VENN (Figure 23).
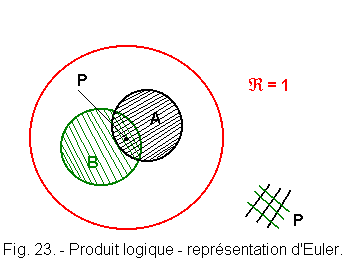
If the set A is the set for which the variable a = 1, and the set B the one for which the variable b = 1, P is the intersection of A and B, and represents the time during which Jacques and Paul are at school, that is to say the set of values of P equal to 1.
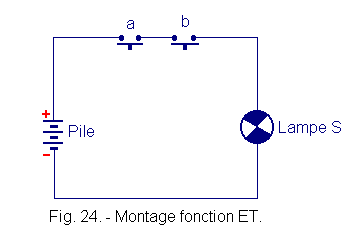
2. 8. 3. - ELECTRICAL ASSEMBLY (Figure 24)
To switch on the lamp, press a AND b simultaneously. Until then, we drew the contacts (term used by logicians) or switches (more general term) as in Figure 24 (representation that is widely used).
Now let's look at the representation of Figure 25.
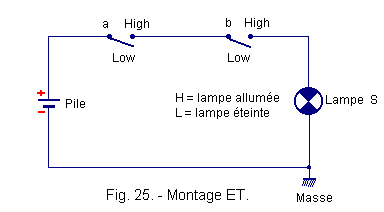
The positive logic corresponds to the physical state contact closed logic state 1, and the physical state contact open logic state 0. The switch is always represented at rest falling from its own weight : what does not is not new.
We have said in the chapter dealing with information in digital systems that the physical phenomenon considered is often a voltage like that of the digital signal that we have described with two well defined high and low levels well determined.
We have adopted the Anglo-Saxon terms High (H) which means high and Low (L) which means low because they are very often used by large component manufacturers such as Texas or in some literatures. We will use this notation in some examples to get you used to these two levels up and down right now.
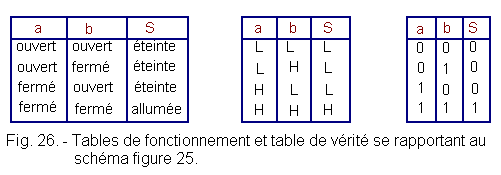
In order for the lamp S to be lit, a and b must be closed, that is to say at the high level from which the tables of Figure 26.
2. 8. 4. - PROPERTIES OF THE LOGIC PRODUCT
Let's associate a binary variable x with 0 and 1, itself or its complement.
Let's give an illustration of these logical associations by means of electrical contacts using the positive logical convention :
![]() 1°) x
.
0 = 0 (Figure 27)
1°) x
.
0 = 0 (Figure 27)
When the x button is pressed, the variable goes to 1 but the current can never go through and S will always be off, hence the truth table in Figure 27.
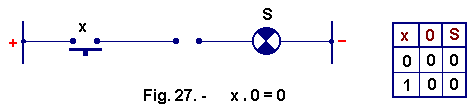
![]() 2°) x .
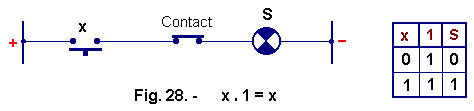
1 = x (Figure 28)
2°) x .
1 = x (Figure 28)
When the x button is pressed, the variable x acts alone on the current, in fact, the contact always at 1 has no influence because it always lets the current flow from where the truth table of the Figure 28.
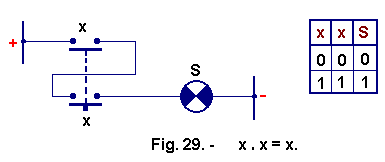
![]() 3°) x .
x = x (Figure 29)
3°) x .
x = x (Figure 29)
When both x buttons are pressed, the variable is at 1 and both contacts are closed so that lamp S lights up. S takes the value of x from which the truth table of Figure 29.
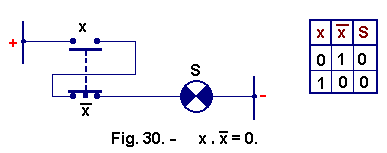
![]() 4°)
4°) ![]() (Figure 30)
(Figure 30)
When the button is pressed, the contact x closes and the contact ![]() opens, the lamp never being fed, therefore always off, hence the truth table of Figure 30.
opens, the lamp never being fed, therefore always off, hence the truth table of Figure 30.
![]() 2. 9. - LOGICAL
SUM OF TWO VARIABLES
2. 9. - LOGICAL
SUM OF TWO VARIABLES
2. 9. 1. - EXAMPLE AND DEFINITION
Suppose now that two children from the village, Paul and Jacques go to school in the neighboring town. When will there be at least one child from the village on the school bus that takes them there ?
Let's summarize the possibilities on the table in Figure 31.
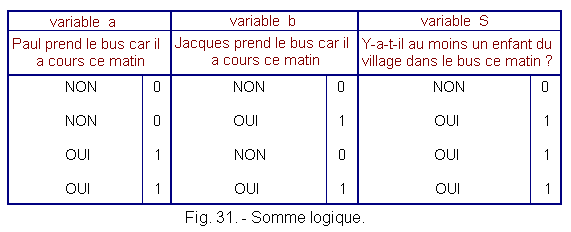
We see that there is a child from the village on the bus when Paul OR Jacques is on the bus, but not only when one or the other is in, but also when there are both.
This is why we say that the function S = f (a, b) is an INCLUSIVE OR (because it includes the case where a and b are present at the same time).
In Boolean algebra (for typographic convenience), we note the operation OR inclusive +.
Example :
a + b = 1 which is stated a OU b is 1.
Unlike traditional algebra, the sign + does not mean more but OR, indeed 1 + 1 = 1 in Boolean algebra !
We have seen previously what is fundamental, that the values taken into account are states and not numbers.
2. 9. 2. - REPRESENTATION OF EULER OR VENN (Figure 32)
Let the logical variables a and b. Let's draw in the frame of reference Â, the surface or the set A within which the variable a is at 1 and the set B inside which the variable b is at 1.
The set in which the variables a or b are at 1, or logical sum, will be the formed surface of the union of the two preceding regions.

In Boolean algebra we will only use notation :
S = a + b that we read S = a OR b
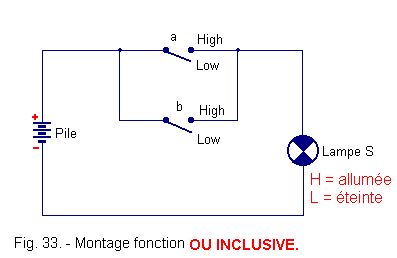
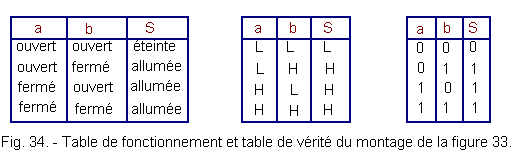
2. 9. 3. - ELECTRICAL ASSEMBLY (figure 33)
We see that it will be enough to close a OR b so that the lamp S lights up (or both at the same time).
We can write S = a + b from which Figure 34 :
2.9.4. - PROPERTIES OF THE LOGIC SUM
Let's associate a binary variable x with 0 and 1, itself or its complement.
For this, we will give an illustration of this logical association by means of electrical contacts (positive logical convention).
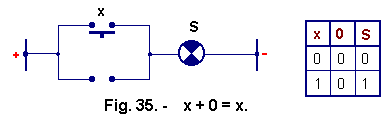
![]() 1°) x + 0 = x (Figure
35).
1°) x + 0 = x (Figure
35).
When the x button is pressed, the variable x becomes 1 and the current supplies the lamp S, hence the truth table of Figure 35.
![]() 2°) x + 1 = 1 (Figure 36)
2°) x + 1 = 1 (Figure 36)
When the x button is pressed, the variable x becomes 1, but this has no effect because the lamp S remains permanently lit, hence the truth table in Figure 36.

![]() 3°) x + x = x (Figure 37)
3°) x + x = x (Figure 37)
The two contacts x are mechanically linked, they close simultaneously, we could replace Figure 37 by Figure 38 : the tables of truth are identical for S with respect to x. One of the x contacts can be deleted.
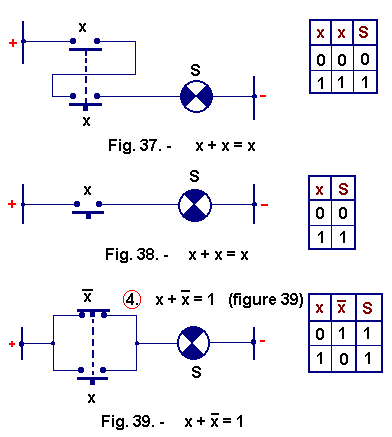
When the current does not pass through x it passes through ![]() and the lamp S is always fed, hence the truth table of Figure 39.
and the lamp S is always fed, hence the truth table of Figure 39.
![]() 2. 10. - GENERALIZATION
OF THE PROPERTIES OF LOGICAL OPERATIONS
2. 10. - GENERALIZATION
OF THE PROPERTIES OF LOGICAL OPERATIONS
We can deduce from the properties seen previously : the summary table (Figure 40).

![]() 1°) Commutativity
1°) Commutativity
We can write that a + b = b + a what is verified in the example of the table (Figure 40) : 0 + 1 = 1 and 1 + 0 = 1 but also a . b = b . a what is true in the same table (Figure 40) : indeed 0 . 1 = 0 and 1 . 0 = 0.
![]() 2°) idempotency
2°) idempotency
For the logical sum we can write : a + a + a = a
For the logical product we can write : a . a . a = a
This property also flows from the table in Figure 40.
![]() 3. a) Distributivity of the logical product with respect to the logical sum
3. a) Distributivity of the logical product with respect to the logical sum
We can easily check that :
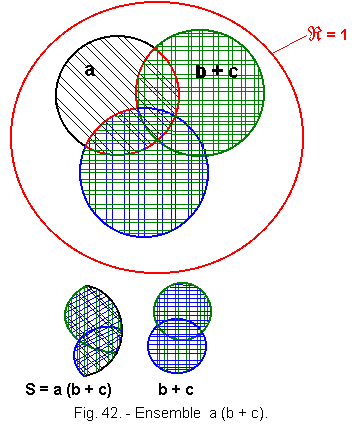
a (b + c) = ab + ac
This property is called the distributivity of the logical product with respect to the logical sum ; it is identical to the distributivity of multiplication over addition in traditional algebra.
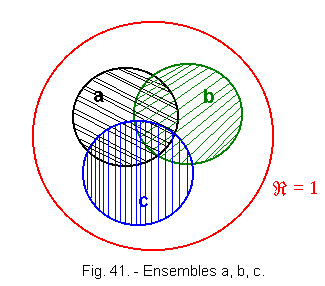
![]() 3. b) Representation of Euler
3. b) Representation of Euler
Figure 41 shows the 3 sets a, b, c.
Draws Figure 42 the set S = a (b + c) intersection of a and b + c.
Let's build now Figure 43, the sets ab and bc and their meeting S = ab + ac.
We see that the surface S is the same in both cases.

![]() 4. a) Absorption
4. a) Absorption
Consider a + ab that we can write a (1 + b), but we know that b + 1 = 1, from which we deduce that a + ab = a (1 + b) = a . 1 = a.
The property a + ab = a absorption property is called.
![]() 4. b) Representation of Euler
4. b) Representation of Euler
Consider the sets a and ab in the Euler representation of Figure 44.
We can easily see that the set a + ab is none other than a.
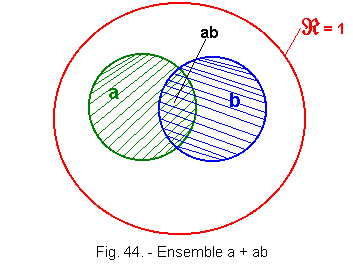
We can say that :
When a sum contains a term and one of its multiples, we can neglect the multiple.
![]() 5. a) Sum of a variable and a multiple of its complement.
5. a) Sum of a variable and a multiple of its complement.
Consider S = a + ![]() b.
b.
By using the corollary of the absorption property which is perfectly valid, one can write :
S = a + ![]() b
= (a + ab) +
b
= (a + ab) + ![]() b
= a + ab +
b
= a + ab + ![]() b
b
from where S = a + b (a +
![]() )
)
or a + ![]() = 1
= 1
from where S = a + b
a + ![]() b = a + b
b = a + b
We can say that when a logical sum is composed of the sum of a variable and a multiple of its complement, we can make the complement disappear.
![]() 5. b) Representation of Euler
(Figure 45)
5. b) Representation of Euler
(Figure 45)
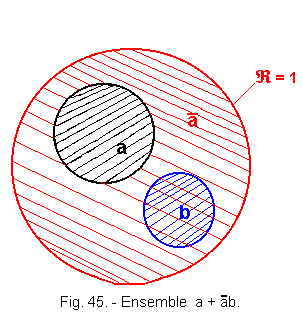
We see that ![]() b is the area corresponding to : b (blue and red hatches) and a
+
b is the area corresponding to : b (blue and red hatches) and a
+ ![]() b is nothing else that a + b.
b is nothing else that a + b.
![]() 6. a) Distributivity of the logical sum with respect to the logical product.
6. a) Distributivity of the logical sum with respect to the logical product.
Consider S = a + bc
The absorption property makes it possible to write :
a = a + ab ; a = a + ac and like a + a = a
We can write a = a + ab + a + ac who becomes a = ab + ac + a
from where S = a + ab + ac + bc
As a = a . a
S = aa + ac + ab + bc
S = a (a + c) + b (a + c)
from where S = (a + b) (a + c)
a + bc = (a + b) (a + c)
![]() 6.b) Representation of Euler
(Figures 46-a et 46-b)
6.b) Representation of Euler
(Figures 46-a et 46-b)
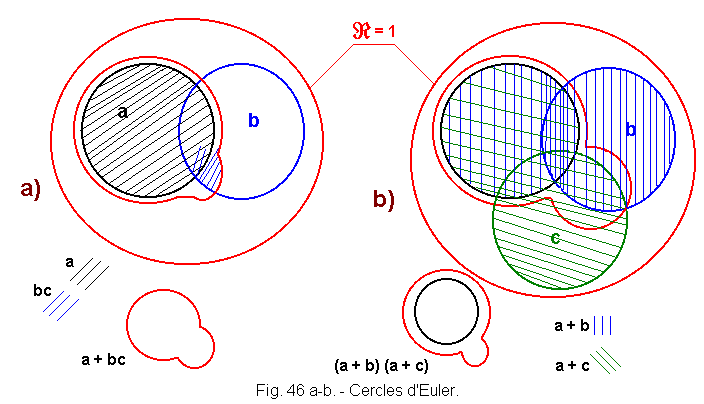
It is easy to highlight by means of circles of Euler Figure 46 the equality (a + bc) = (a + b) (a + c).
![]() 2. 11. - GENERAL
USE SYMBOLS (AMERICAN REPRESENTATION)
2. 11. - GENERAL
USE SYMBOLS (AMERICAN REPRESENTATION)
![]() 1.) Function YES
1.) Function YES
It will be materialized by a wire most often.
It can be materialized by the symbol of the buffer (Figure 47). We will talk about the buffer later.
![]() 2.) Function NO (Figure 48)
2.) Function NO (Figure 48)
The symbol of the function NO is characterized by the addition of a bubble which shows that the output of the logical operator is inverted.
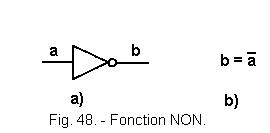
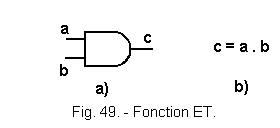
![]() 3.) Function AND (Figure 49)
3.) Function AND (Figure 49)
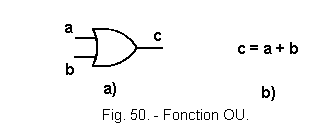
![]() 4.) Function OR (Figure 50)
4.) Function OR (Figure 50)
It should be noted that these symbols are those of logical operators contained in the integrated circuits, for example, and although they require a power supply, it is not represented.
 Click here for the next lesson or in the summary provided for this purpose. Click here for the next lesson or in the summary provided for this purpose. |
|
 Previous Page Previous Page |
 Next Page Next Page |
Nombre de pages vues, à partir de cette date : le 27 Décembre 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.
 Logical sum of two variables
Logical sum of two variables