Notions about sets - Algebra Logic :
1. - NOTIONS ON THE SETS
1. 1. - SETS
We call together any collection of objects or beings taken at random or having common properties.
Example :
![]() all plants
all plants
![]() the set of celestial objects
the set of celestial objects
![]() all animals
all animals
![]() all carnivores
all carnivores
![]() all mammals
all mammals
![]() the set of integers.
the set of integers.
In mathematics, we represent a set by a surface.
1. 2. - INTERSECTION OF TWO SETS (Figure 1)
We call the intersection of two sets A and B the set I composed of all the objects common to A and B.
The hatched set I constitutes the intersection of sets A and B (Figure 1).
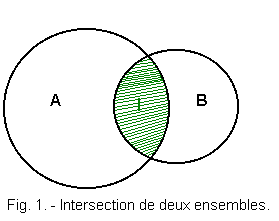
In the mathematical theory of sets, we write I = A n B and we state I equal A inter B.
In Boolean algebra, for typographic convenience, we write on écrit :
I = A . B
What we say
I equals A AND B
Indeed, if, for example, A is the set of carnivores and B is the set of mammals, I will be the set of mammalian AND carnivorous animals.
1. 3. - DISJOINT ASSEMBLY (figure 2)
Disjoint sets are two sets A and B that have no common element.
We will say that if for example A is the set of mammals and B the set of plants, that A and B are two disjoint sets.
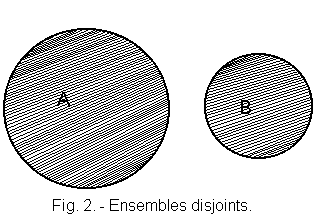
There is nothing in common between the two.
1. 4. - MEETING OF TWO SETS (Figure 3)
We call the union of two sets A and B, the set R composed of elements belonging to at least one set A and B.
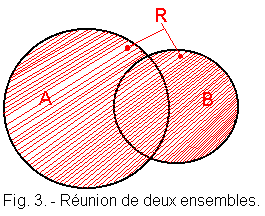
The hatched set R constitutes the union of A and B. In set theory, we write R = A u B and state R equal to union B.
In Boolean algebra, for typographic convenience, we write :
R = A + B
What is stated R = A OR B
Indeed, if, for example, R is the set of living beings, To all plants, and B to all animals, we can say that living beings R are plants A OR animals B.
1. 5. - INCLUSION, PARTLY, PART (Figure 4)
1. 5. 1. - EXAMPLE AND DEFINITION
If each element of a set A belongs to the set F, we can say that set A is included or contained in set F.
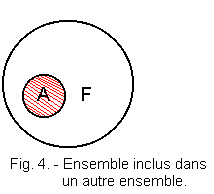
We write A ⊂ F. We state A is included in F.
Indeed, if, for example, F is the set of animals, and to all mammals, we say that A is a subset of F, or that all mammals A is only a part of set of animals F.
1. 5. 2. - EQUIVALENT SCRIPTURES A ⊂ F
a) - The writing A . F = A is illustrated in Figure 5.
We can say, indeed, that all beings that are both animals AND mammals are all mammals simply, see A.
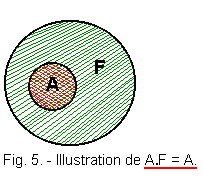
We can see that the intersection of A ET F is indeed A.
A n F = A or A . F = A
But we also see that A is well included in F.
b) - The writing A + F = F is illustrated in Figure 6.
We can say that A u F = F or A + F = F.
Set A is well included in F.

This amounts to saying for example that a being, belonging to all mammals A, or belonging to all animals F, belongs in any case to all animals F.
1. 6. - COMPLETION OF ONE SET IN RELATION TO ANOTHER (Figure 7)
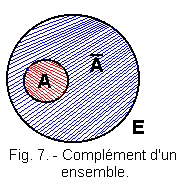
Let a set A be included in a set E.
The set of elements belonging to E and not belonging to A is the complement of A with respect to E.
We will note ![]() and we will state A barre the complement of A with respect to E.
and we will state A barre the complement of A with respect to E.
If E for example is all animals, and A to all carnivores (or animals eating meat), we can say that vegetarian animals (or not eating meat) belong to the set ![]() .
.
1. 7. - REFERENTIAL (Figure 8)
Suppose that the set A (p) is the set of elements having the property p included in a set Â.
The set  is called a repository.
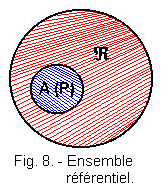
If no element of the set A (p) has the desired property, we will call A (p) together empty.
The set ![]() (p)
is the complement of A (p) with respect to Â.
(p)
is the complement of A (p) with respect to Â.
By convention, in Boolean algebra, the repository is designated by 1 and the empty set by 0.
If the empty set is ![]() and the repository Â
= 1, we can write :
and the repository Â
= 1, we can write :
A + ![]() = Â =
1
= Â =
1
1. 8. - EXAMPLE OF REPRESENTATION OF BINARY NUMBERS (Figure 9).
We call a binary digit a number that can only have two values 1 or 0.
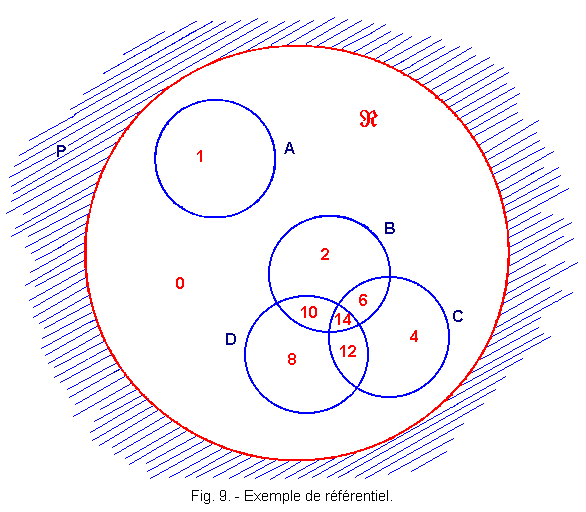
Consider the referential  constituted by the portion of the plane P delimited by a closed curve. The plan is divided into two areas that do not overlap. The repository contains the binary logical variables taking the values 1 or 0.
If there exists a, b, c, d, such that a = 1 for a belonging to A, b = 1 for b Î B, c = 1 for c Î C and d = 1 for d Î D, we will say that a = 0, b = 0, c = 0 and d = 0 for a, b, c, d not belonging to A, B, C, D ; that is to say, part of the empty set 0, (Î means belonging to, Ï means not belonging to).
We can say that inside the repository there are nine zones numbered from 0 to 14 such that a, b, c, d take the values of Figure 10.
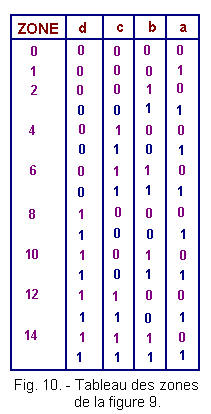
We can see that all combinations of a, b, c, d, do not exist, as shown in Figure 9.
We will see later that some binary variables (terms defined in the next chapter) can not take in an electrical scheme, for example, all existing values due to technological impossibilities.
![]() 2. - LOGICAL ALGEBRA
2. - LOGICAL ALGEBRA
2. 1. - STATE CONCEPT
"The state is the way things are."
We say that a salad is green and a tomato is red. But you can never add a green salad and a red tomato.
On the other hand, it is safe to say that there are two plants (whose colors are different).
If we now consider a red bicycle and a red automobile, we can say that they are red.
We therefore see that if operations can be performed taking into account states (here colors) they are not arithmetic operations, or traditional algebraic, because the result is not characterized by a number but by a state (here a color).
In the previous examples we have chosen two different characteristic colors, red and green : our logic of reasoning is therefore a two-state logic.
"A door must be opened or closed."
It is the same thing for an electrical contact, for which there are only two positions (or two states) : open or closed.
An electromagnetic relay such as those used in telephone exchanges or automatic exchanges is at rest (not excited) or at work (excited).
A shutter in a pneumatic pipe is open or closed, the same will be true for a hydraulic valve.
A proposition such as Paul is at school can only have two answers or logical states :
![]() YES Paul is at school
YES Paul is at school
![]() NO Paul is not at school.
NO Paul is not at school.
2. 2. - BOOLEAN BINARY VARIABLE
In the example above, we can say : Is Paul at school ? Yes or NO. Nothing prevents you from assigning the answer YES of the value 1 and the answer NO of the value 0.
We can say that the variable "Paul is in school" has two states : YES state 1, NO state 0 (Figure 11).
A Boolean variable will be any quantity that can take only two values : 1 or 0.

Let's now look at the length of the day :
When Paul is at school, the days are 24 hours.
When Paul is not at school do days make 24 hours ? OUI.
We can say that in our history, the duration of the day is a constant.
If we arbitrarily set state 1 to YES, the state of the day will always be 1.
We will call Boolean constant any Boolean quantity that always keeps the same value, 1 or 0.
2. 3. - FUNCTION OF A VARIABLE
When two Boolean variables, a and b, are linked by a relation, such that a value of a corresponds to a value of b, we say that b is a function of a and we write :
b = f (a)
Example :
"If it's nice, I'll go for a walk."
Here the variable "walk" is a function of the variable "good weather". Indeed, if it rains I will not go for a walk, but if the weather is fine I will go.
2. 4. - FUNCTION OF SEVERAL VARIABLES
For simplicity, consider the case of a function of two variables.
A function will be called two variables when the variable c, for example, depends on both the value of a variable a, as well as a variable b. We say that c is a function of a and b we write c = f (a, b).
Example :
"If the weather is nice and I'm in better health, I'll go for a walk."
The variable "walk" depends on the variable "good weather" and the variable "better health". Because, it takes me to go for a walk that the weather is beautiful and my health is better.
2. 5. - FUNCTION OF FUNCTION
If d is a function of c, we can write d = F (c) but as c = f (a, b) we write :
d = F [ f (a, b) ]
We say that d is function of function of a and b.
Example :
"If I go for a walk, I'll take the dog."
The variable "output of the dog" is a function of the variable "walk" which, as we saw above is a function of the variable "good weather" and the variable "health".
2. 6. - FUNCTION YES (Fgure 12)
2. 6. 1. - EXAMPLE AND DEFINITION
Suppose now that when the weather is nice, Paul will play ball and when it rains he goes to school.
Call respectively a and b the variable "good weather" and the variable "Paul plays ball."
If we assign the YES answer of 1 and the NO answer of 0, we can construct the array (Figure 12) :

We see that the variable "Paul plays ball" is at 1 when the variable "good weather" is at 1. It is at 0 when the variable "good weather" is at 0.
We can write Paul plays ball = f (good weather) and as the variable "Paul plays ball" always takes the same value as the time variable, we say that the function f is a function YES.
We write a = b.
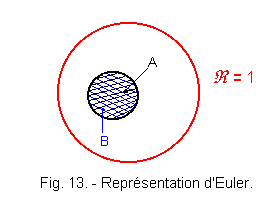
2. 6. 2. - REPRESENTATION OF EULER OR VENN (Figure 13)
We say that two variables a and b are equal, when they are represented by the same points of the repository, that is to say if the contours which define them are merged.
![]() 2. 6. 3. - ELECTRICAL
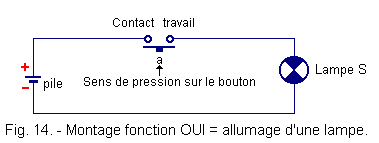
ASSEMBLY : CONVENTIONS (Figure 14)
2. 6. 3. - ELECTRICAL
ASSEMBLY : CONVENTIONS (Figure 14)
The push-button switch of Figure 14 is always on a principle diagram represented at rest, that is to say the push button which makes it maneuver unpowered. By convention, it represents the pusher so that it falls into position by its own weight (contact shown horizontal).
In Figure 14, we see a work contact, that is, that closes at work (when activated). It is therefore open at rest as in Figure 14.
By convention also we make correspond in positive logic :
![]() in the physical state closed contact the logical state 1
in the physical state closed contact the logical state 1
![]() in the physical state open contact the logical state 0
in the physical state open contact the logical state 0
![]() We call the "contact variable" : a,
because this variable is active at 1, that is to say lets pass the current from the stack when pressing the pusher : it is a working contact.
We call the "contact variable" : a,
because this variable is active at 1, that is to say lets pass the current from the stack when pressing the pusher : it is a working contact.
The lamp comes on (state 1) when switch a is closed (state 1).
The lamp is off (state 0) when switch a is open (state 0).
By state "0" or state "1" is defined the electrical state of an element.
2. 6. 4. - TABLE OF TRUTH
So far we have studied logical propositions as we make them every time we speak ; that is to say, sentences.
Now, in practical examples made with contacts, and illustrating each function, we map a logical state to a physical state.
In the example of Figure 14, we can call "a" input variable and "S" output variable or receiver. As a general rule, a receiver will be a motor, a lamp or any controlled device. An input variable will be a contact or a transducer or sensor that can be summarized as a contact.
This is why truth tables boil down to input and output variables assigned the corresponding logical state. For Figure 14, we obtain the truth table (Figure 16).
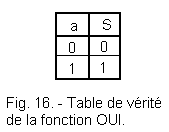
We will use lowercase letters for input and uppercase variables for output variables..
2. 7. - INVERSION FUNCTION, NO, NOT
2. 7. 1. - EXAMPLE AND DEFINITION
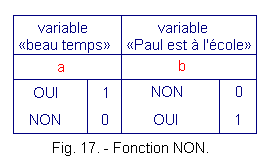
Let us now examine the relation or function that links the "good weather" variable to the "Paul is in school" variable, which we will call respectively a, b (Figure 17).
We see that the variable "Paul is in school" is at 0 when the variable "good weather" is at 1 and vice versa. We can therefore say that the function f which links the variable "Paul is in school" to the variable "good weather" is the inversion function which is also called complement.
We write
b = ![]() that we state b = a bar.
that we state b = a bar.
2. 7. 2. - REPRESENTATION OF EULER OR VENN (FIGURE 18)
Let A be a set included in a referential set  of the binary numbers 0 or 1.
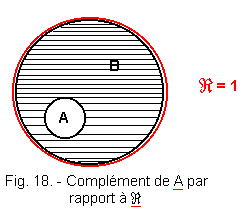
The set of elements belonging to  and not belonging to A, is called complement of A with respect to Â.
The hatched set (Figure 18) is the complement of A with respect to the  set B.
One can designate the complement of A by ![]() ,
one deduces whereas B =
,
one deduces whereas B = ![]() .
.
Since the set  is the set of bits (we call bit a binary digit of the English "binary digit") at 1 or 0, we can say that if the variable has a ΠA and if the variable b ΠB.
if a = 0 ---------> b = ![]() = 1
= 1
if a = 1 ---------> b = ![]() = 0
= 0
2. 7. 3. - ELECTRICAL ASSEMBLY : CONVENTIONS (Figure 19)
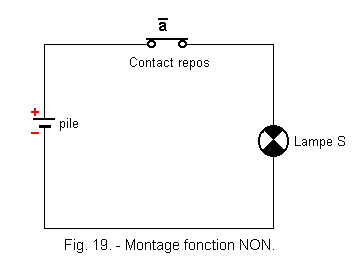
The contacts being always represented at rest, (falling by their own weight), the contact shown in Figure 19 is always closed at rest : it will be called rest contact.
We will keep the convention stated about Figure 14 namely :
![]() electrical state of the contact : closed -----> logical state 1
electrical state of the contact : closed -----> logical state 1
![]() electrical state of the contact :
open
-----> logic state 0
electrical state of the contact :
open
-----> logic state 0
We will call this convention a positive logic.
In positive logic is called the "rest contact" variable ![]() this variable is a closed contact that is to say in logic state 1 when it is not actuated, that is to say when is not active and we will say that
this variable is a closed contact that is to say in logic state 1 when it is not actuated, that is to say when is not active and we will say that ![]() = 1, the lamp S will then be lit and its logical state will be 1.
= 1, the lamp S will then be lit and its logical state will be 1.
Conversely, when ![]() is pressed the contact will open from where the logical state 0 : in this case
is pressed the contact will open from where the logical state 0 : in this case ![]() = 0 ; the lamp S will be extinguished and its logical state will be 0.
= 0 ; the lamp S will be extinguished and its logical state will be 0.
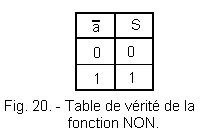
We can therefore write S = ![]() that can be summarized by the truth table (Figure 20).
that can be summarized by the truth table (Figure 20).
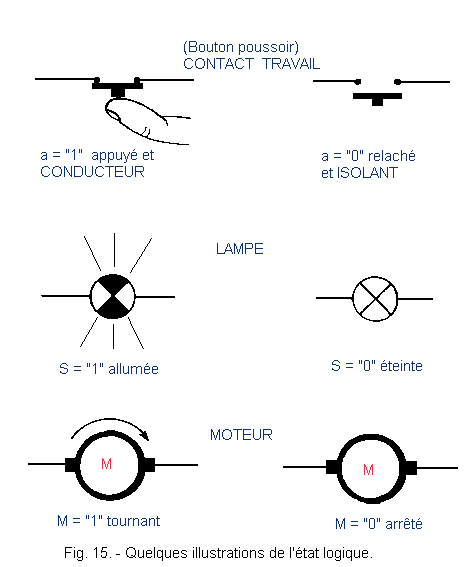
The state "0" or state "1" is defined as the electrical state of an element (Figure 21).

We
advise you before going further to compare this figure with the figure 15 in order to understand the difference of notation between contact work and contact rest for which one calls the variable ![]() .
.
 Click here for the next lesson or in the summary provided for this purpose. Click here for the next lesson or in the summary provided for this purpose. |
|
 Previous Page Previous Page |
 Next Page Next Page |
Nombre de pages vues, à partir de cette date : le 27 Décembre 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.
 Logical algebra
Logical algebra