Digital / Analog converterAnalog and Digital Signal Conversions - Digital / Analog Converter :
In the latter theory, we will examine another family of widely used circuits : «converters». Let's first see what their roles are and what their applications might be.
1. - CONVERSIONS OF ANALOG AND DIGITAL SIGNALS
There are many applications in which digital devices have to communicate with the outside world, for example when it is necessary to control the temperature, the pressure, the speed, the humidity, the level of a liquid, the illumination, etc. ...
These physical quantities are analog data that can take all the possible values.
These quantities are measured by sensors that transform them into analog electrical signals.
Whenever a digital circuit has to process an analog data, it is necessary that the latter be translated in a language understandable by the circuit, that is to say in binary code.
Analog / digital converters are intended for this purpose.
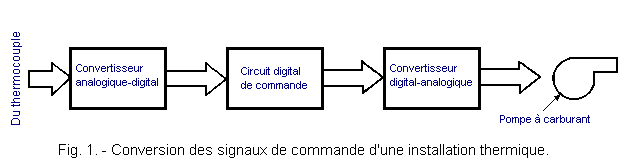
Suppose a temperature control system controlled by a computer. First of all, it is necessary to measure the temperature by means of a sensor, for example a thermocouple. To keep the temperature constant, it is necessary to control the flame of the boiler, by varying the flow of fuel by means of a pump.
But the pump can not be controlled directly by a digital circuit which delivers only two levels : 1 and 0. The control must be continuous, proportional to the flow of fuel that one wishes to obtain.
It is therefore necessary to transform the coded binary commands delivered by the computer into an analog electrical signal. This operation is performed by a digital / analog converter (D / A).
In the same way, the analog signal delivered by the thermocouple can not be assimilated by the computer. In this case, it is necessary to insert between the sensor and the computer, an analog / digital converter (A / D), Figure 1.
Other examples of use of converters in all fields and particularly in communications (radio, television, telemetry, etc.) are encountered. Consider the case of a telephone call. When one speaks in front of the microphone, the vibrations of the air are transformed into an analogical electric signal, more or less ample depending on the intensity of the sound.
This signal, appropriately amplified, is transmitted along the telephone line and on arrival, it is transformed by the loudspeaker into audible vibrations (Figure 2).
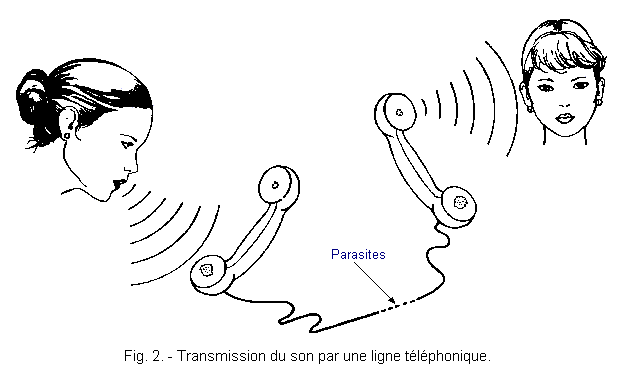
Along the line, the signals are often altered by electromagnetic interference, causing very annoying noise and background noise.
In a completely analog transmission system, such as the one just described, it is quite difficult to avoid or eliminate these parasites.
With a digital transmission system, it is much easier to solve this problem (Figure 3).
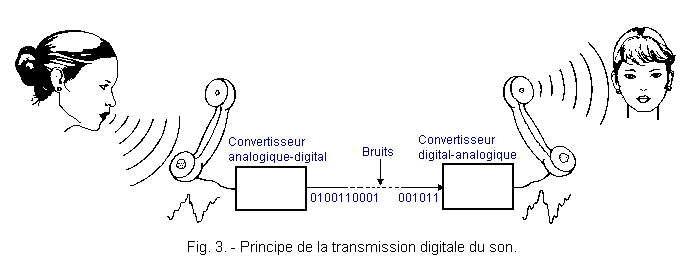
Between the microphone and the telephone line, an analog / digital converter is inserted. A series of binary numbers is thus obtained on the line indicating at each instant the amplitude of the signal to be transmitted. In this way, it is much easier to combat noise since only two levels (0 and 1) must be distinguished.
CMOS circuits have a noise immunity equal to 0.45 times Vcc. Under these conditions, by feeding the circuits with a voltage Vcc of 10 volts, parasites of an amplitude less than 4.5 volts are not able to influence the behavior of the converters and are easily eliminated. To restore the sound at the other end of the line, it is obviously necessary to use a digital / analog converter.
There are, in addition, other methods that can process the digital signals to eliminate parasites that might have infiltrated the transmission.
Another example of converter use is found in modern aircraft driven by an on-board computer.
All the necessary data (altitude, pressure, speed, outside temperature, etc. ...) are measured by sensors. This data is converted into binary numbers and transmitted to the on-board computer which performs all calculations according to the pilot's indications (Figure 4).
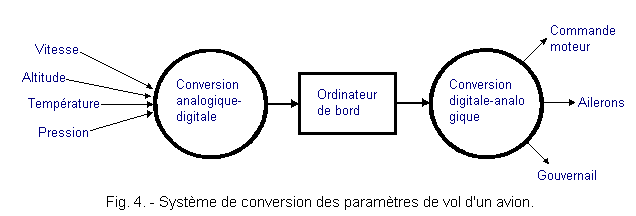
The on-board computer delivers binary number sequences which must be converted into analog data by means of appropriate converters.
It is obvious that converters are not only useful, but that in very many cases they are indispensable. The use of converters tends to become more widespread since digital circuits are more stable, less expensive and in general create fewer problems than analog circuits.
2. - THE
DIGITAL / ANALOG CONVERTER
The operation of a digital / analog converter (D / A) can be compared to that of a potentiometric circuit of the type shown in Figure 5.
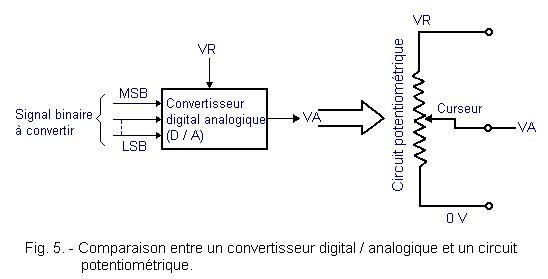
The converter receives a digital signal on as many input terminals as there are bits in the binary number.
At the bottom, there are the least significant bits (LSB = Least Significant Bit) and at the top (Figure 5), the most significant bits (MSB = Most Significant Bit) arrive.
The input binary signal determines at output a voltage VA proportional to the digital value represented by the input signal, just as in the potentiometric circuit, VA depends on the position of the cursor.
The converter also receives a reference voltage VR. In the comparison, this voltage corresponds to VR existing between the extreme terminals of the potentiometer. In both cases, VR represents a level with respect to which VA output voltages are referenced.
In the potentiometric system, VA can take any value between 0 volts and VR.
In the converter, one observes a similar behavior, but in output, VA progresses by leaps or in «staircase». Each rise of a step corresponds to a unit increase of the numerical input value.
It can therefore be said that the voltage VA of the converter is still of digital type, but compared to the binary signals on the input terminals, it already acquires an analog look.
To determine the value of the voltage VA delivered by the converter, the formula VA = D x VR is used.
D represents a fractional coefficient corresponding to the digital value present at the input terminals.
A converter having four input terminals, can receive sixteen different bit combinations ranging from the number 0000 to the number 1111.
Each unit increase in the input binary number corresponds to a 1 / 16 increase in VR on the VA output.
The table of Figure 6 gives the value of the coefficient D for a converter with four input bits.
| Rang
4
MSB |
Rang
3
3rd bit |
Rang
2
2nd bit |
Rang
1
LSB |
Coefficient D |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 / 16 |
| 0 | 0 | 1 | 0 | 2 / 16 = 1 / 8 |
| 0 | 0 | 1 | 1 | 3 / 16 = 1 / 8 + 1 /16 |
| 0 | 1 | 0 | 0 | 4 / 16 = 1 / 4 |
| 0 | 1 | 0 | 1 | 5 / 16 = 1 / 4 + 1 / 16 |
| 0 | 1 | 1 | 0 | 6 / 16 = 1 / 4 + 1 / 8 |
| 0 | 1 | 1 | 1 | 7 / 16 = 1 / 4 + 1 / 8 + 1 / 16 |
| 1 | 0 | 0 | 0 | 8 / 16 = 1 / 2 |
| 1 | 0 | 0 | 1 | 9 / 16 = 1 / 2 + 1 / 16 |
| 1 | 0 | 1 | 0 | 10 / 16 = 1 / 2 + 1 / 8 |
| 1 | 0 | 1 | 1 | 11 / 16 = 1 / 2 + 1 / 8 + 1 / 16 |
| 1 | 1 | 0 | 0 | 12 / 16 = 1 / 2 + 1 / 4 |
| 1 | 1 | 0 | 1 | 13 / 16 = 1 / 2 + 1 / 4 + 1 / 16 |
| 1 | 1 | 1 | 0 | 14 / 16 = 1 / 2 + 1 / 4 + 1 / 8 |
| 1 | 1 | 1 | 1 | 15 / 16 = 1 / 2 + 1 / 4 + 1 / 8 + 1 / 16 |
The bit of rank 1 (LSB), when it takes the value 1, determines a value VA equal to 1 / 16 of VR.
Under the same conditions (bit = 1), the bit of rank 2 corresponds to 1 / 8 of VR, the bit of rank 3 to 1 / 4 of VR and the bit of rank 4 (MSB) to 1 / 2 of VR.
To find the value of the coefficient D corresponding to any binary number, it suffices to add the coefficients assigned to the ranks in which we find the value 1.
Example : 1001 corresponds to the coefficient D = 1 / 2 + 1 / 16 = 9 / 16.
In practice, the ratio VA / VR ratio should be represented as a function of the input bit number. Figure 7 shows the transfer characteristic of a 3 bits input converter.
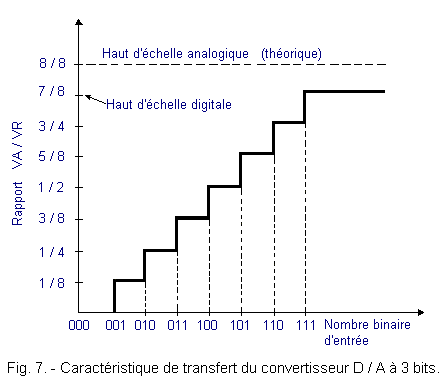
It should be noted that the maximum value VR (8 / 8) is not reached. The highest combination that we can have is 111. The coefficient D that we obtain in this case is :
-
1 / 2 for the MSB
-
1 / 4 for the 2ème bit
-
1 / 8 for the LSB.
The sum D for the highest combination is therefore equal to : 1 / 2 + 1 / 4 + 1 / 8 = 7 / 8, value beyond which one can not go, or rather beyond which one can only go by adding other bits, so other input levels.
For example with 4 bits, we get 16 levels from 0000 to 1111 and, as we saw above, each level or step is distant from the previous 1 / 16 of VR.
Figure 8 shows the transfer characteristic for a 4 inputs D / A converter. In this way, we manage to reach the top 15 / 16 scale. In cases of this kind, it is usually said that the nominal circuit resolution has been increased.
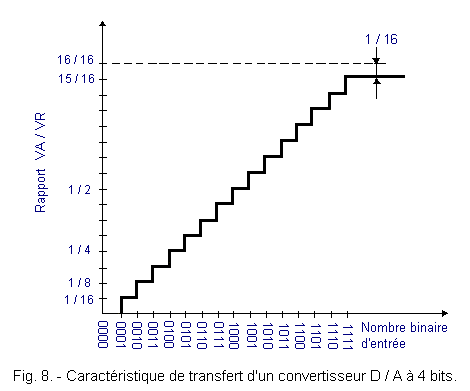
The nominal resolution is the amplitude of the steps and coincides with the weight of the least significant bit (LSB) : 1 / 16 in the case of a 4 bits input.
NOTE : The resolution should not be confused with the accuracy of the converter which will be discussed a little further.
2. 1. - DIGITAL / ANALOG CONVERTER
A BRIDGE DIVIDER OF VOLTAGE
Figure 9 shows the principle of a digital / analog converter with voltage divider bridge.
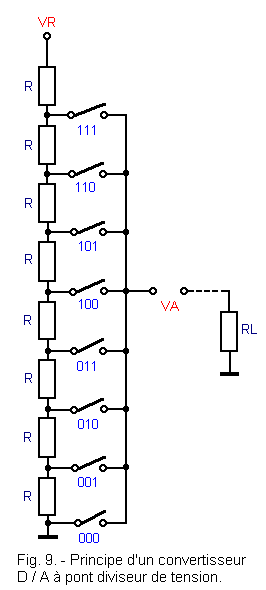
The digital input consists of a number of switches equal to the number of possible combinations with three bits, minus one, that is to say :
23 - 1 = 8 - 1 = 7
It is assumed that in this circuit only one switch can be closed at a time.
Thus, at each closed switch, there corresponds an analog voltage VA proportional to the binary number represented by the switch.
Note that the binary value assigned to each of the switches is equal to the number of resistors connected between the switch considered and the ground.
This circuit has two disadvantages. The first lies in the fact that it is necessary to have as many switches minus one as there are possible binary combinations (remember that for only 8 bits, there are already 256 combinations which would require 255 switches). On the other hand, the load resistor RL, of no infinite value, unbalances the entire divider bridge and the output voltages are no longer exactly proportional to the digital input values.
For these reasons, a more complex circuit using an operational amplifier is used in practice. Let's open a parenthesis to give some essential details on this type of circuit.
 Click here for the next lesson or in the summary provided for this purpose. |
 Top of page |
|
Previous Page |
 Next Page |
Nombre de pages vues, à partir de cette date : le 27 Décembre 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.