Codes and Decoders - Number Codes

**Signets :**
Numeration codes	Binary number at the corresponding Decimal value	The bits
	Footer

Codes and Decoders - Number Codes - Bits :

In this theory, you will review concepts, already discussed in theory 7, but in a simpler form. These notions concern codes and numeration systems.

You will then see how to move from one code to another and display the information.

1. - CODES AND DECODERS

1. 1. - INFORMATION AND CODES

Traffic lights (Figure 1) are used to direct traffic within cities.

Indeed, each road user receives coded information on the conduct he must adopt.

Orange : slow down

Red : stop

Green : go

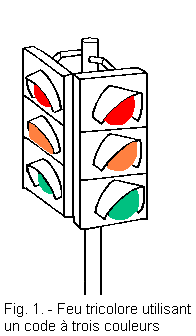
In everyday life, communication involves a coded language.

The national number of the Social Security is, for example, a code which allows to recognize the individuals in order subsequently to be able to realize by a computer all the operations relating to their medical reimbursements under the social insurance. An example is given in Figure 2.

Language and writing are also means of communication in code. This supposes that there is a rule binding the one who writes and the one who reads the message.

Insects communicate with each other in different ways, that is with different codes :

Bees have different ways of flying to drive other bees to a specific place or warn them of danger, this is called bee dancing.

Some animals emit chemicals called «pheromones» that allow for example to mark their territory, or to attract their partner ; others like fireflies send bright messages.

All these examples could multiply to infinity.

Computers or digital circuits can not do without codes to communicate with each other.

Since, as we have seen, digital circuits operate with two levels : high (H) and low (L) ; all codes can only use two basic information related to these two levels 1 and 0 (Figure 3).

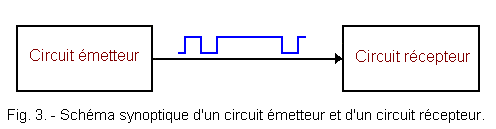
However, the possibilities offered by combinations of 1 and 0 are very numerous. Their choice will depend on the desired applications.

In the same way, the letters of the alphabet are not numerous but they nevertheless make it possible to compose an infinity of words and this in many languages.

Unfortunately, it is impossible to know all the languages of the world, so it is necessary to have interpreters.

In digital circuits, the problem is the same. For a circuit using an x code to be able to converse with a circuit using a code y, it will be necessary to have an interpreter which we will call decoder x / y (Figure 4) or decoder y / x according to the direction in which the conversion of code s' will perform (hence the terms «x to y» or «y to x» that you will encounter later).

The decoder translates the information of one code into another, hence also the term transcoder.

We will examine the main numeric codes and the corresponding decoders.

1. 2. - NUMBER CODES

The information processed in the digital circuits is represented by levels H and L representing logical values 1 and 0.

We have seen that these two signs are sufficient to express information in binary code.

We also know that the numbering system we use every day is different. This is the decimal system that uses 10 signs from 0 to 9.

1. 2. 1. - ORIGIN OF THE DECIMAL NUMBER

When the ancients wanted to count objects (here ears of wheat), they had to imagine numbers and the corresponding signs.

An example is given in Figure 5.

Each quantity of objects corresponds to a number symbolized by a graphic sign. But very quickly, the problem became impossible because every time we added an object, we had to invent a new symbol.

The signs from 0 to 9 are familiar to us, but they could be different, so the Romans used the sign V for 5 and for 10 the sign X that we picked up here.

The signs Ñ and invented for the purposes of the course mean for Ñ, 11 and for , 12.

To count to 10 000, it would take 10 000 signs and to count to infinity an infinity of signs.

The Chaldeans found the solution.

The idea was to be limited to ten signs from 0 to 9, that is to say as much as the fingers of the hands and to express each number as great was it by a combination of these ten signs.

Thus having only 10 signs, arrived at 9 was decided to start again at 0 and to indicate 1 for the first ten.

Thus for X, we can write 10 = 1 tens + 0 units ;

for Ñ, we can write 11 = 1 tens + 1 unit ;

for , one can write 12 = 1 decade + 2 units.

Thus, the signs 20 signify : 2 tens + 0 units.

We see that this system makes it possible to write numbers whose structure is such that for 3472₁₀ for example, this number means :

3 (10³) + 4 (10²) + 7 (10¹) + 2 (10⁰)

The first digit on the right is that of units of weight 10⁰ = 1, the second from the right has a weight of 10¹ = 10, it is the number of tens, the third from the right has a weight of 10² = 100, that's the number of hundreds, and so on.

We see that the weight of the numbers is multiplied by 10 each time the figure shifts one row to the left. We will call 10, base of the system.

Thus, in 1 000 = 10 x 10 x 10 = 10³, 10 is the base and 3 the exponent which indicates how many times the base has to be multiplied by itself.

1. 2. 2. - BINARY NUMBER

In the binary number, as we have only two digits, the base will be 2 and we will be able to take up the problem of wheat ears as shown in Figure 6.

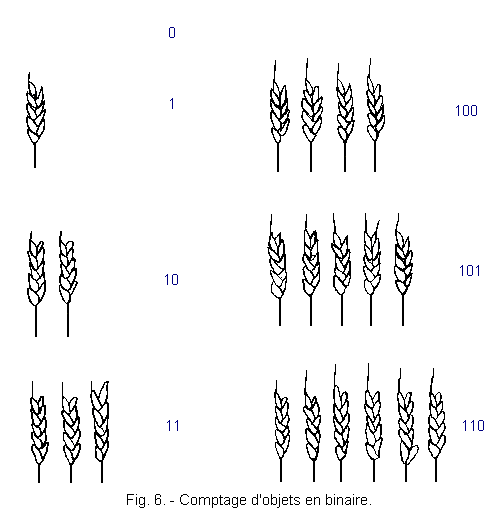
So for no ears of wheat, we have : 0 x 2⁰ = 0
for an ear of wheat 1 x 2⁰ = 1
for two ears of wheat 1 (2¹) + 0 (2⁰) = 10
for three ears of wheat 1 (2¹) + 1 (2⁰) = 11
for four ears of wheat 1 (2²) + 0 (2¹) + 0 (2⁰) = 100
for five ears of wheat 1 (2²) + 0 (2¹) + 0 (2¹) = 101
for six ears of wheat 1 (2²) + 1 (2¹) + 0 (2¹) = 110

These two types of numeration, binary and decimal, constitute a type of code called weighted code.

In the table of Figure 7, we find the first twenty numbers expressed in weighted decimal code and weighted binary code.

To express numbers larger and larger, it is necessary to have more and more numbers.

**Fig. 7. - Numbers from 0 to 20 represented in both decimal and binary weighted codes**.
Number	Weighted decimal code	Weighted binary code
0	00	00000
1	01	00001
2	02	00010
3	03	00011
4	04	00100
5	05	00101
6	06	00110
7	07	00111
8	08	01000
9	09	01001
10	10	01010
11	11	01011
12	12	01100
13	13	01101
14	14	01110
15	15	01111
16	16	10000
17	17	10001
18	18	10010
19	19	10011
20	20	10100

A combination of 4 binary digits can be one of 16 numbers between 0 and 15.

Note :

Each binary number is represented in this figure by a five-digit code consisting of adding to the left the significant 0 necessary.

It is useful to know what is the maximum number that can be represented with a fixed number of binary digits. It can be determined by reading the maximum numerical value when each digit is 1 as shown in Figure 8. This gives the example of a number of 4 binary digits.

The maximum number that can be represented with n binary digits is : 2ⁿ- 1.

1. 3. - PASSING A BINARY NUMBER TO THE CORRESPONDING DECIMAL VALUE

Just give each binary digit its weight and then add the weights of the different digits.

If we take for example the number 10112 :

10112 = 1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰

= 1 x 8 + 0 x 4 + 1 x 2 + 1 x 1 = 8 + 0 + 2 + 1 hence 10112 = 1110

To do the opposite operation, that is to say to go from a decimal number to the corresponding binary number, it is possible to divide this number by two.

The remains of each division will constitute the digits of the binary number by reading them from the last. Remember that the rest is 0 when the dividend is even and 1 when it is odd.

For the number 277, we obtain for example :

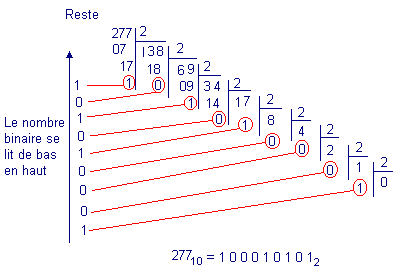
So at 27710 is the binary number 1000101012. Indeed, if we break down the number according to the binary code, we get :

1000101012 = (1 x 2⁸) + (0 x 2⁷) + (0 x 2⁶) + (0 x 2⁵) + (1 x 2⁴) + (0 x 2³) + (1 x 2²) + (0 x 2¹) + (1 x 2⁰)

= (1 x 256) + (0 x 128) + (0 x 64) + (0 x 32) + (1 x 16) + (0 x 8) + (1 x 4) + (0 x 2) + (1 x 1)

= 256 + 16 + 4 + 1 = 277

To all the binary numbers written with the numbers 0 and 1 correspond as many decimal numbers written with decimal digits.

For example, the binary number 1112 whose value is equal to seven (710) could also represent the decimal number 11110 whose value is equal to 111.

In order to avoid confusion of this kind, the index 2 is written for the binary numbers and the index 10 or the decimal numbers.

By doing so, we will have :

11110 if the number is decimal and is 111 ;
1112 if the number is binary and is 710.

1. 4. - THE BITS

The binary numbers are formed of digits 0 and 1. These binary digits are called «binary digit», abbreviated «bit».

Subsequently, the term bit has a broader meaning than that of a binary digit. It indicates more generally the unit of information that can be stored in a flip-flop.

Any information of any type can be expressed for an appropriate sequence of bits. Thus one can digitize speech (digital telephone), writing (word processing), music (digital disk), mathematical or financial calculation (calculators, computers and billers).

In computers, each piece of information is broken down into a succession of bits. No computer can process more than one bit at a time.

In compensation, by its extraordinary speed, it is able to perform logical or arithmetic operations so quickly that it performs incredibly complex tasks in an extremely short time.

In general, the word bit is often used to indicate the number of stages, for example a counter. We commonly speak of counters or shift registers 4 bits, 8 bits, 12 bits which means that there are 4, 8, 12 flip-flops.

Click here for the next lesson or in the summary provided for this purpose.	Top of page
Previous Page	Next Page

Nombre de pages vues, à partir de cette date : le 27 Décembre 2019

Mon audience Xiti

Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.

Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.

Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.