One can thus write : Intensity = Tension / Resistance and by replacing the words by the corresponding letters :

I = V / R

Example : It is applied to a circuit, having a resistance (R) of 5 Ohms and a voltage (V) of 15 volts ; calculate the intensity of the current (I) absorbed by this circuit :

We know that :     I = V / R

We will have     I = 15 / 5 = 3 ampères

The intensity of the current absorbed by the circuit is therefore 3 amperes.

Now compare the three formulas obtained from the statements of Ohm's Law :

• The first R = V / I, represents a division of the voltage by the intensity whose result gives a value of resistance ;

• The second V = R x I, represents a multiplication of the resistance by the intensity whose result gives a value of tension ;

• The third I = V / R, represents a division of the voltage by the resistance whose result is an intensity value.

Since there are three distinct formulas, we may be led to think that there are three laws of Ohm, this conclusion would be erroneous. In reality, the three formulas are equivalent to each other because they represent three aspects of the same link

This statement can easily be demonstrated with randomly selected examples, which show that all values that satisfy only one of the three formulas also satisfy the other two.

In the three examples above, we have already found that the values of 15 volts, 3 amps and 5 ohms satisfactorily satisfy the formulas R = V / I ; V = R x I and I = V / R.

Now consider another example chosen at random.

A circuit having a resistance (R) of 150 ohms is traversed by a current of an intensity (I) of 2 amperes ; calculate the value of the voltage (V) applied to this circuit.

To calculate the value of the voltage, it is necessary to choose between the three formulas, that which presents, to the left of the sign = the letter V, which represents the tension. We see immediately that the second formula is the right one ; therefore, following the usual procedure, we will have :

V = R x I

V = 150 x 2 = 300 volts

The voltage applied to the circuit is therefore 300 volts. We can now ensure that these same values of 150 ohms, 2 amps and 300 volts also meet the other two formulas of Ohm's Law.

Using the first formula, we get, in effect :

R = V / I

R = 300 / 2 = 150 ohms

The result of 150 ohms is exactly what we expected for a voltage of 300 volts and an intensity of 2 amps, based on the previous calculations.

Using the third formula, we get :

I = V / R

I = 300 / 150 = 2 amps

This result of 2 amps is also that obtained previously.

We could take many examples similar to this one.

Each of them would always demonstrate that the three values : voltage, intensity and resistance of a circuit satisfactorily satisfy the three formulas. You can then ask what are the purposes of three equivalent formulas, derived from Ohm's law, linking the same values to each other. Would not one formula suffice ? No, because each of them makes it possible to carry out a precise calculation quickly :

• With the first formula (R = V / I), we can calculate the value of the resistance when those of the voltage and the intensity are given ;

• With the second formula (V = R x I), we can calculate the value of the voltage by knowing the values of the resistance and the intensity.

• With the third formula (I = V / R), we can calculate the value of the intensity by knowing those of the tension and the resistance.

It is interesting to note that the number of equivalent formulas obtained from Ohm's law is three, just as three different letters appear in the formulas corresponding to the three characteristic quantities of the circuit (voltage, intensity, resistance).

This concordance of numbers is not a coincidence.

If the number of quantities connected to each other were three, four or five ..., we would obtain formulas containing three, four or five letters and the same number of equivalent formulas, all equally capable of expressing completely the link between the quantities considered.

If, for all the laws of electronics, we were to follow the same procedure that we adopted for Ohm's law, we would obtain an incredible quantity of formulas, which would make the study excessively long and arduous.

One is therefore led to ask a question : is it really necessary to draw all the equivalent formulas of a law, since they all mean the same thing ?

The answer is quite reassuring : it is not necessary to draw directly from the statement of a law all the equivalent formulas : it is enough to draw one only, whatever it is, and from this one we can then reconstitute all the others, by means of the simple rules of mathematical calculation.

In this perspective, we will now establish some of the simple rules that will allow us to move from one given formula to another.

  2. - THE LITERAL CALCULATION

 2. 1. - RULES

To prepare ourselves for the rules that allow us to move quickly and easily from one formula to another, consider the three formulas of Ohm's law in a different light.

In the first place, let us call the first member, the part of the formula to the left of the sign =, and the second member, the part on the right.

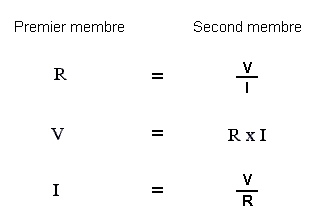
This convention is valid for any mathematical expression consisting of two parts linked together by the relation of equality. When the = sign appears in a mathematical expression, it is called equality, and the following rule is still valid :

Rule 1 : If we interchange between the 2 members of a tie, we obtain a new equality equivalent to the first.

Based on this rule, we can write indifferently :

R = V / I     or     V / I = R

V = R x I     or     R x I = V

I = V / R     or     V / R = I

Indeed, if we consider the values corresponding to the letters (15 volts, 3 amps and 5 ohms) that were found during the first three exercises, we do not find any difference between :

5 = 15 / 3     or     15 / 3 = 5

15 = 5 x 3     or     5 x 3 = 15

3 = 15 / 5     or     15 / 5 = 3

When a mathematical expression and in particular a formula contains a multiplication, we can apply the following rule :

Rule 2 : One does not change the value of a multiplication, if one invert the order of the factors.

By combining this rule with the previous one, we can write, for example, the second formula of Ohm's Law in the following four ways, all equally correct :

In fact, by taking the previous numerical example, we find that the admissible values in the first of the four formulas indicated here, are also valid for the three others :

So far we have considered the appearance of the formulas by changing the place letters without changing the values. Now we are going to do something more : based on a few other rules, we will change the values while maintaining equality between the first and second members.

Rule 3 : If you multiply the two members of a tie by the same number, you keep the tie.

Consider the first form of Ohm's law.

Multiply the first and the second member of the formula R = V / I by the same number, for example 7, and, let's take our circuit with the value R is 150 ohms, that of V of 300 volts and that of I of 2 amps ; we will have :

R x 7  =  V / I x 7

150 x 7  =  300 / 2 x 7

1050  =  150 x 7

1050  =  1050

The result clearly tells us that despite the multiplication, the two members are always equal to each other.

Rule 4 : If we divide the two members of a tie by the same number, we maintain equality.

Consider the second formula of Ohm's law : V = RI. Let's take the same values as in the previous example and divide each term by 50 :

V / 50  =  R x I / 50

300 / 50  =  150 x 2 / 50

6  =  300 / 50

6  =  6

This result shows that despite the divisions made, the two members always remain equal to each other.

In the two previous examples, the numbers 7 and 50 were randomly selected, but any number could be used to demonstrate the accuracy of rules three and four.

Here are two other rules that allow you to quickly move from a given formula to its equivalents :

Rules 5 : If a member of an equality is constituted by a division, the divisor may be transferred to the other member as multiplying factor. .

Take the third form of Ohm's law, I = V / R. Based on the rule just stated, we obtain :

I x R = V

Example : In a circuit the value of the voltage (V) is equal to 60 volts and that of the resistor (R) to 15 ohms. The intensity (I) obtained by dividing 60 by 15 has the value :

I = V / R

4 = 60 / 15

4 = 4 

Now let R (divisor in the 2nd member) in the first member as a multiplier. We have :

I x R = V

4 x 15 = 60

60 = 60

These two results demonstrate that, in passing from the first form to the second, we maintain equality.

Rule 6 : If a member of an equality is a multiplication, any one factor may be transferred to the other member as divisor.

Example :

The three results show that we have kept the equality of the two members from one form to another.

The operations by means of which a letter can be transferred from one location to another in a mathematical expression, preserving the equality of the two members, take the name of literal calculation (or algebraic calculation), by analogy with the calculation name numerical (or arithmetic) that has been given to operations performed with numbers.

We will now clarify the concepts that have been exposed here, by means of an example of application of literal computation to the field of electronics.

2. 2. - APPLICATION OF THE LITERAL CALCULATION

We will see that the electrical resistance of a conductor depends on its length, its section and its resistivity. (Resistivity is a characteristic of the material constituting the conductor).

If we want to translate this statement into mathematical formulas, we find ourselves extremely embarrassed. Indeed, it is not specified how much the resistance of the conductor varies when one increases or decreases the length, the section or the resistivity. To overcome this obstacle, it is necessary to refer to a more precise statement, such as : one obtains the resistance of a conductor by multiplying its resistivity by its length and dividing the product obtained by its section.

This statement may be abbreviated as follows : 

Let us agree to represent the resistance by the letter R, the resistivity by the Greek letter r, the length of the conductor by the lowercase letter l, and its section by the capital letter S, we obtain the following formula :

R = r x l / S

Using this formula, we can then calculate the resistance of any conductor, knowing its length, section and resistivity.

If the resistivity is expressed using the unit of measurement ohm-centimeter, the length in centimeters and the section in square centimeters, the value of the resistance will be expressed in ohms.

Example : A cylindrical bar has a length (l) of 60 centimeters, a section (S) of 3 square centimeters and is made of a material having a resistivity (r) of 2 ohm-centimeter ; calculate its resistance (R).