Tension Alternative :
Nous avons vu dans la précédente leçon comment on représente graphiquement un courant alternatif, et quelles sont les grandeurs qui le caractérisent ; nous allons maintenant examiner la tension alternative.
1. - TENSION ALTERNATIVE
Pour déterminer la forme de la tension alternative, nous devons nous rappeler qu'elle est liée par la loi d'OHM au courant qui parcourt la résistance ; comme nous connaissons déjà la forme du courant alternatif, il nous est facile de chercher l'allure de la tension qui détermine le passage de ce courant dans la résistance.
Voyons, par exemple, comment on peut représenter graphiquement la tension alternative qui fait circuler le courant alternatif dans un circuit comprenant une résistance de 5 ohms (figure 1-a).
Nous observons d'abord qu'au début de la période (0 s), à la moitié (0,1 s) et à la fin de la période (0,2 s), le courant est nul : si à ces instants, le courant ne circule pas dans le circuit, cela signifie que la tension fournie par le générateur est également nulle.
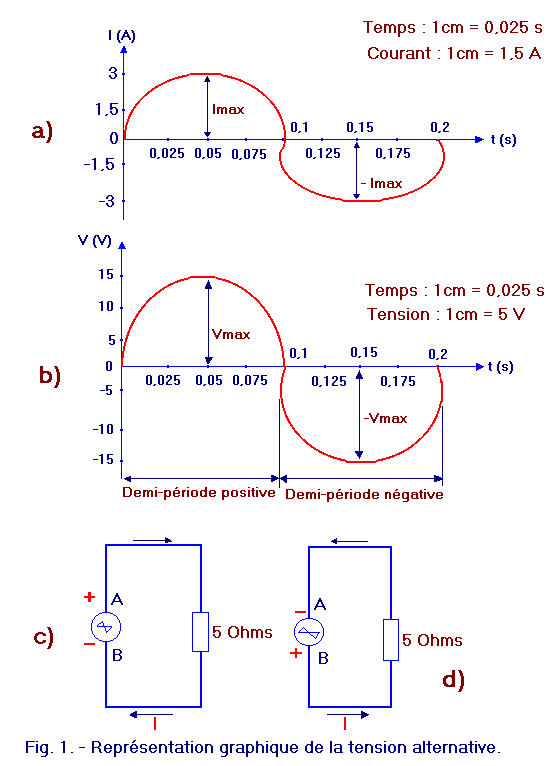
Quand, au contraire, le courant atteint la valeur maximale (Imax) après 0,05 s, et (- Imax) après 0,15 s, la tension atteint aussi à ces instants la valeur maximale correspondante Vmax et -Vmax (certains livres d'électroniques noterons Imax par IM et Vmax par VM).
Puisque la valeur maximale du courant est de trois ampères, il faut pour faire passer ce courant dans une résistance de cinq ohms, une tension qui, d'après la loi d'OHM, est donnée par le produit de la valeur de la résistance par celle du courant : la valeur maximale de la tension est donc de 5 x 3 = 15 V.
De même, nous pouvons obtenir la valeur de la tension en un autre instant quelconque, en multipliant la valeur de la résistance par celle du courant prise en cet instant.
Les valeurs ainsi obtenues sont reportées sur le diagramme de la figure 1-b. Sur l'axe horizontal de ce diagramme, les temps sont indiqués de la même manière que pour le courant, c'est-à-dire que chaque centimètre correspond à 0,025 s. Sur l'axe vertical du diagramme, les tensions (U) exprimées en volts (V) sont maintenant indiquées ; 1 cm correspond à 5 V, comme le précise l'inscription "1 cm = 5 V" reportée en haut et à droite.
Comme la valeur Imax du courant est atteinte au bout de 0,05 s, la valeur Vmax de la tension correspond à ce même moment ; on procède de la même façon pour la valeur -Imax, mais puisque cette valeur se trouve sous l'axe horizontal, la valeur correspondante de la tension -Vmax est également sous cet axe.
Si l'on reporte de la même façon les autres valeurs de la tension, par exemple celles prises au bout de 0,025 s, 0,075 s, 0,125 s et 0,175 s, on obtient un certain nombre de points qui permettent de tracer la ligne de la figure 1-b en les joignant ; cette courbe indique l'allure de la tension alternative. Comme on pouvait s'y attendre, c'est aussi une sinusoïde, et nous pouvons donc dire que la tension alternative a, elle aussi, une forme sinusoïdale.
(Pour vous faciliter la tâche, nous reportons le même schéma ci-dessous).

Comme nous l'avons déjà fait pour le courant, nous pouvons donc considérer la tension alternative comme une succession de cycles tous identiques, dans chacun desquels se répètent toujours les mêmes valeurs.
Le temps que met la tension pour accomplir un cycle est appelé période de la tension alternative et il se divise lui aussi en deux demi-périodes égales, l'une positive et l'autre négative ; dans la première, les valeurs de la tension sont indiquées par des nombres positifs, tandis que dans la deuxième, les mêmes valeurs sont indiquées par des nombres négatifs.
Ce fait nous indique que le générateur inverse ses polarités à chaque demi-période ; sur la figure 1-b, les valeurs des tensions fournies par le générateur sont indiquées par des nombres positifs quand celui-ci a ses polarités comme sur la figure 1-c, tandis que les valeurs des tensions sont indiquées par des nombres négatifs lorsque le générateur intervertit ses polarités comme sur la figure 1-d.
Notons que, après avoir désigné par A et B les pôles du générateur, on a considéré que le courant positif était celui qui sortait du pôle A du générateur, comme sur la figure 1-c, et que le courant négatif était au contraire, celui qui entrait dans le générateur par le pôle A, comme sur la figure 1-d. On a de même considéré que la tension était positive ou négative lorsque le pôle du générateur désigné par A était positif, comme sur la figure 1-c, ou négatif, comme sur la figure 1-d.
Il faut se rappeler ce procédé car il sera encore utilisé dans cette leçon.
Nous observons maintenant que la tension alternative doit avoir évidemment la même période que le courant, comme on le vérifie d'ailleurs immédiatement en comparant les figures 1-b et 1-a : le courant et la tension accomplissent le même cycle en une seconde et ils ont donc la même fréquence.
Pour caractériser une tension alternative, nous devons donc indiquer, non seulement sa période ou sa fréquence, mais également sa valeur : comme pour le courant, on indique la valeur efficace que l'on obtient en divisant par 1,41 la valeur maximale de la tension alternative (valable seulement pour un régime sinusoïdal).
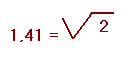
Quand nous disons, par exemple, que la tension du réseau disponible dans nos habitations a une valeur de 110 V ou bien de 220 V, nous nous référons à la valeur efficace de cette tension ; la tension indiquée sur les appareils électriques qui fonctionnent au courant alternatif est la valeur efficace de la tension avec laquelle on doit alimenter ces appareils.
On appelle valeur efficace d'une tension alternative sinusoïdale aux bornes d'une résistance R, la valeur d'une tension continue dont le courant produirait les mêmes effets calorifiques que le courant alternatif sinusoïdal dans la même résistance R et pendant le même temps. De cette façon, on établit une équivalence entre la tension alternative et la tension continue, en ce qui concerne les effets calorifiques produits par les courants qu'elles mettent en circulation.
Dans la pratique, cela signifie, par exemple, qu'un fer à souder prévu pour une tension de 220 V peut être alimenté soit par une tension alternative qui a une valeur efficace de 220 V, soit par une tension continue de 220 V. Dans les deux cas, le fer à souder produit la même quantité de chaleur car la tension alternative fait circuler dans sa résistance un courant dont la valeur efficace est égale à celle de celui que fait circuler la tension continue.
Le courant continu qui circule dans le fer à souder peut être obtenu, selon la loi d'OHM, en divisant la tension continue par la résistance du fer à souder ; de la même façon, si l'on divise la valeur efficace de la tension alternative appliquée au fer à souder par sa résistance, on peut obtenir la valeur efficace du courant qui l'alimente.
Nous voyons donc qu'avec les valeurs efficaces, nous pouvons effectuer les calculs relatifs au courant alternatif comme s'il s'agissait d'un courant continu, non seulement en ce qui concerne la chaleur produite par le courant, mais aussi pour l'emploi de la loi d'OHM.
Mais il faut bien se rappeler que l'équivalence entre le courant alternatif et le courant continu n'est valable qu'en ce qui concerne l'effet thermique : cela signifie que nous ne pouvons considérer le courant alternatif comme un courant continu que dans les circuits formés exclusivement d'éléments résistifs qui transforment l'énergie électrique en chaleur.
Dans les leçons précédentes, nous avons vu d'autres éléments, tels les condensateurs et les bobines, qui ne dissipent pas l'énergie électrique mais l'emmagasinent en créant respectivement un champ électrique ou magnétique.
Pour les condensateurs et les bobines, l'équivalence entre le courant alternatif et le courant continu n'est plus valable, puisque ces éléments ne donnent pas lieu à la production de chaleur. Cependant, dans le cas des circuits qui comprennent des condensateurs ou des bobines, on indique également la valeur efficace de la tension et du courant, mais toujours en référence à l'effet thermique.
Lorsque l'on dit, par exemple, qu'une bobine est parcourue par un courant alternatif d'une valeur efficace de 2 A, on indique un courant alternatif qui produirait, s'il traversait une résistance, la même quantité de chaleur que celle produite par un courant continu de 2 A.
Nous devons donc nous rappeler que, pour les grandeurs alternatives et sinusoïdales, on indique toujours la valeur efficace, même lorsqu'il s'agit de circuits dans lesquels aucun effet thermique ne se produit.
Comme nous l'avons vu précédemment, la résistance offerte par l'élément résistif au courant alternatif s'obtient en divisant la valeur efficace de la tension par celle du courant, de même qu'en régime continu. Cela signifie que "les résistances" ont le même comportement en régime continu qu'en régime alternatif, car elles offrent au passage des deux courants une résistance qui est égale pour les deux régimes au rapport de la tension par le courant.
Au contraire, les condensateurs et les inductances demanderont à être examinés séparément suivant le régime appliqué.
![]() 2. - REPRÉSENTATION
VECTORIELLE DES GRANDEURS ALTERNATIVES
2. - REPRÉSENTATION
VECTORIELLE DES GRANDEURS ALTERNATIVES
La représentation utilisée jusqu'à présent, consistant à dessiner la sinusoïde qui indique les valeurs de la tension ou du courant durant un cycle complet, n'est pas très commode ; on a donc adopté un autre système de représentation qui à l'avantage de mettre en évidence beaucoup de propriétés des grandeurs alternatives qui n'apparaissent pas clairement sur le dessin de la sinusoïde.
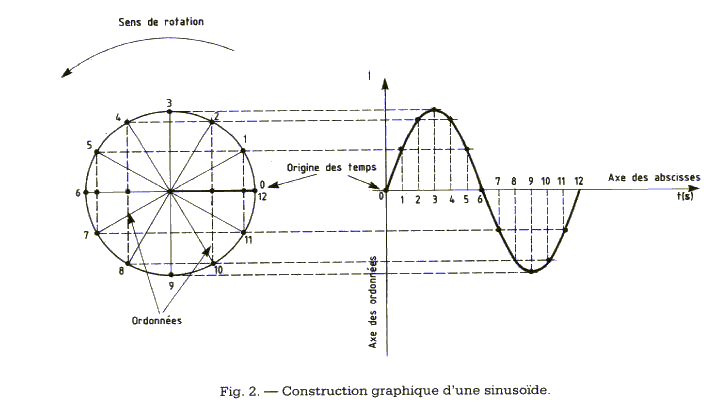
La sinusoïde représentant une grandeur alternative est dessinée comme illustré figure 2, en faisant tourner un segment de longueur égale au maximum de la sinusoïde et en reportant point par point les ordonnées de son extrémité.
Donc pour représenter une tension ou un courant alternatif, il suffit de reporter dans un repère orthogonal les projections perpendiculaires sur l'axe des ordonnées du vecteur tournant aux instants choisis.
Cette méthode de tracé porte le nom de représentation vectorielle où les grandeurs alternatives sinusoïdales sont obtenues grâce à un vecteur caractérisé par :
- une longueur proportionnelle à l'amplitude maximale (ou élongation) de la grandeur alternative et sinusoïdale ; si par exemple, on veut représenter une tension sinusoïdale de valeur Vmax = 300 V, on peut choisir de prendre une échelle avec 1 cm pour 100 V et dessiner un vecteur de longueur 3 cm correspondant à 300 V.
- une vitesse constante en sens antihoraire dont un tour complet représente la période de la grandeur sinusoïdale. Ainsi le vecteur accomplit en une seconde un nombre de tours égal à la fréquence de la grandeur considérée.
- une position pour laquelle son ordonnée représente la valeur de la grandeur considérée à cet instant précis.
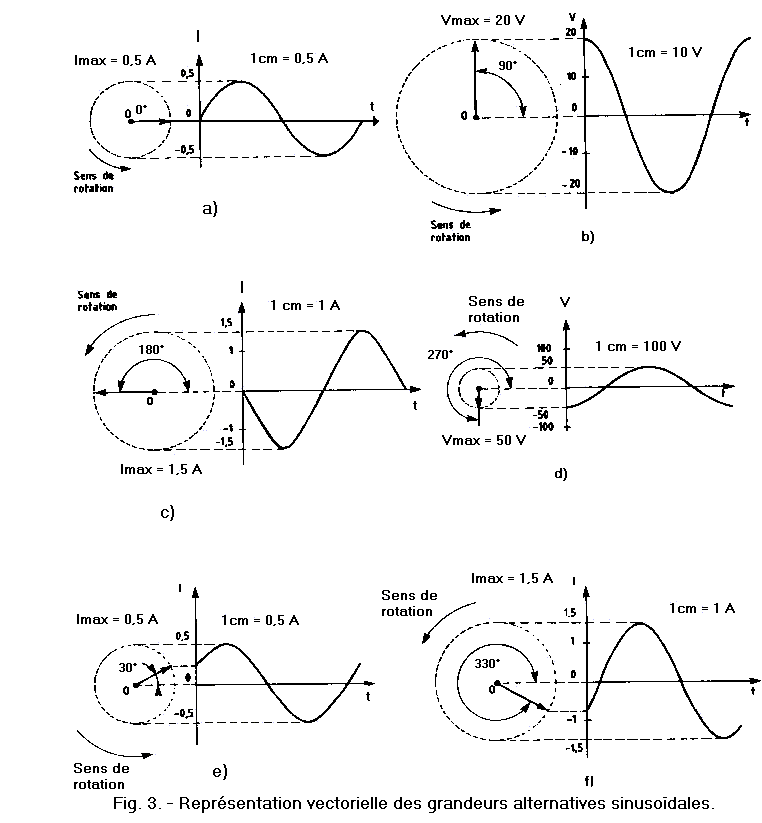
Pour mieux comprendre cette méthode, nous donnons six exemples sont reportés figure 3.
La figure 3-a représente un courant alternatif sinusoïdal de valeur maximale Imax = 0,5 A correspondant à 1 cm sur l'axe des ordonnées. Le vecteur représentatif de 1 cm de long est à l'origine des temps (0s) en position horizontale, signifiant que son ordonnée est nulle, tout comme l'est la valeur de la sinusoïde. Ce vecteur ayant effectué un tour complet, les valeurs de son ordonnée prise à des instants précis et reportées dans le repère orthogonal, décriront la forme sinusoïdale du courant de la figure 3-a.
La figure 3-b représente une tension alternative sinusoïdale de valeur maximale Vmax = 20 V correspondant à 2 cm sur l'axe des ordonnées. Le vecteur représentatif de 2 cm de long en avance de 90° par rapport à l'origine des temps (0s) est en position verticale, signifiant que son ordonnée est maximale et positive, tout comme l'est la valeur de la sinusoïde. Ce vecteur ayant effectué un tour complet, les valeurs de son ordonnée prises à des instants précis et reportées dans le repère orthogonal décriront la forme sinusoïdale du courant de la figure 3-b.
La figure 3-c représente un courant alternatif sinusoïdal de valeur maximale Imax = 1,5 A où 1 cm correspond ici à (1 A) sur l'axe des ordonnées. Le vecteur représentatif de 1,5 cm de long placé à 180° de l'origine des temps (0s) est en position horizontale, orienté vers la gauche (contraire à celui de la figure 3-a), signifiant ainsi que la valeur de la sinusoïde est nulle. Seulement cette fois, la sinusoïde débutera par des valeurs négatives quand le vecteur effectuera son tour complet en sens antihoraire ; le tracé reste le même que les précédents (figures 3-a et 3-b).
La figure 3-d représente une tension alternative sinusoïdale de valeur maximale Vmax = 50 V où 1cm correspond ici à 100 V sur l'axe des ordonnées. Le vecteur représentatif de 0,5 cm de long positionné à 270° de l'origine des temps (0s) est en position verticale, orienté vers le bas (contraire à celui de la figure 3-b) car la sinusoïde débute par un extremum (valeur maximale) négatif.
On s'aperçoit dans les exemples donnés que le vecteur est positionné à l'endroit où commence la sinusoïde pour indiquer sa valeur à cet instant précis (t = 0s). Il faut savoir que l'angle formé par le vecteur et l'axe horizontal est atteint suivant un temps (t) qui sera reporté sur l'abscisse (axe horizontal), voir figure 2.
Sur l'exemple de la figure 3-e, le vecteur du courant Imax = 0,5 A de la figure 3-a est représenté avec une avance de 30° par rapport à l'origine des temps. Sur la figure 3-f, le vecteur du courant Imax = 1,5 A est représenté avec une avance de 330° par rapport à l'origine des temps.
En règle générale, il est plus intéressant, à un instant donné, de comparer la position des vecteurs que de connaître leur valeur.
La figure 4 illustre les vecteurs représentatifs de la tension et du courant dans un circuit purement résistif comme celui de la figure 1. Puisque les deux sinusoïdes débutent à l'origine des temps, les deux vecteurs sont horizontaux et superposés.
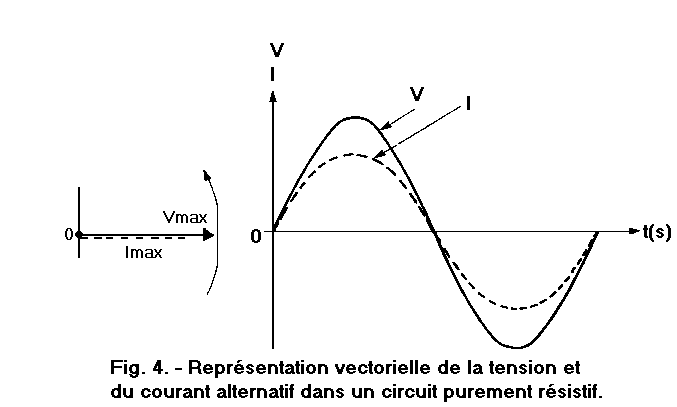
Les deux vecteurs, tournant autour du point 0 à la même vitesse, engendrent deux sinusoïdes (V,I) de même allure, obtenues par l'ordonnée des deux vecteurs tournants.
Quand les valeurs de deux grandeurs atteignent en même temps les extremums (maximum et minimum) et se joignent sur l'axe des abscisses pour s'annuler, on dit de ces deux sinusoïdes qu'elles sont en phase.
Donc lorsque deux grandeurs alternatives de même fréquence sont en phase, les vecteurs représentatifs sont superposés et tournent à la même vitesse.
A chaque tour le vecteur décrit un angle de 360° ; s'il accomplit un tour en une seconde, sa vitesse de rotation sera de 360° par seconde (360° / s), pour "n" tours par seconde sera de n x 360° par seconde.
Généralement, les angles sont exprimés en radian : angles qui interceptent un arc de cercle de longueur égale au rayon. Comme 360° correspondant à 2 n radians, on peut exprimer la vitesse de rotation par 2n x n radians par seconde.
Un cycle d'une grandeur alternative correspond à un tour complet du vecteur représentatif et le nombre de tours "n"
effectués en une seconde représente le nombre de cycles par seconde de la sinusoïde, appelé encore fréquence (F).
La vitesse du vecteur représentatif sera appelée pulsation (symbole ![]() oméga-unité de mesure en rad / s) et exprimée par la relation :
oméga-unité de mesure en rad / s) et exprimée par la relation :
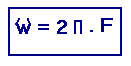
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente
|
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Représentation vectorielle des grandeurs
alternatives
Représentation vectorielle des grandeurs
alternatives