Formulaire 1. 2. - Électronique :
1. 2. - ÉLECTRONIQUE
![]() FORMULE 74 -
(loi d'OHM) : Calcul de la résistance d'un circuit connaissant la tension appliquée et l'intensité du courant.
FORMULE 74 -
(loi d'OHM) : Calcul de la résistance d'un circuit connaissant la tension appliquée et l'intensité du courant.
Calculer la résistance d'un circuit connaissant la tension et l'intensité du courant
Énoncé : La résistance, exprimée en ohms, s'obtient en divisant la tension exprimée en volts par l'intensité du courant, exprimée en ampères (Voir théories 1 et 1.2 dans la rubrique sommaire électronique).
R = V / I
R = résistance en W (ohm)
V = tension en V (volt)
I = intensité du courant en A (ampère)
Exemple :
Données : V = 150 V ; I = 0,2 A
Résistance du circuit : R = 150 / 0,2 = 750 W
OBSERVATION : La formule 74 peut aussi s'appliquer en exprimant la tension et l'intensité du courant respectivement en sous-multiples (ou en multiples) du volt et de l'ampère ; en particulier, on peut exprimer la tension en millivolts (mV ; 1 mV = 0,001 V) et l'intensité du courant en milliampères (mA ; 1 mA = 0,001 A) et ainsi la résistance sera exprimée en ohms.
Cependant, si la tension est exprimée en volts et l'intensité du courant en milliampères (mA ; 1 mA = 0,001 A), la résistance sera exprimée en kilo-ohms (kW ; 1 kW = 1 000 W). On exprime quelquefois la tension en volts et l'intensité du courant en microampères (µA ; 1 µA = 0,000 001 A) ; dans ce cas, en appliquant la formule 74, on obtient la résistance exprimée en mégohms (MW ; 1 MW = 1 000 000 W).
![]() FORMULE 75 - (loi
d'OHM) : Calcul de la tension appliquée à un circuit connaissant la résistance
et l'intensité du courant.
FORMULE 75 - (loi
d'OHM) : Calcul de la tension appliquée à un circuit connaissant la résistance
et l'intensité du courant.
Calculer la tension d'un circuit connaissant la résistance et l'intensité du courant
V = RI
V = tension en V (volt)
R = résistance en W (ohm)
I = intensité du courant en A (ampère)
(Cette formule est tirée de la formule 74).
Exemple :
Données : R = 1500 W ; I = 0,1 A
Tension appliquée : V = 1500 x 0,1 = 150 V
OBSERVATION : La formule 75 peut aussi s'appliquer en exprimant la résistance et l'intensité du courant respectivement avec les sous-multiples de l'ohm et de l'ampère ; on peut en particulier exprimer la résistance en kilo-ohms (kW) et l'intensité du courant en milliampères (mA) et ainsi la tension sera exprimée en volts.
![]() FORMULE 76 - (loi
d'OHM) : Calcul de l'intensité du courant connaissant la résistance et la tension appliquée au circuit.
FORMULE 76 - (loi
d'OHM) : Calcul de l'intensité du courant connaissant la résistance et la tension appliquée au circuit.
Calculer l'intensité d'un circuit connaissant la résistance et la tension
I = V / R
I = intensité du courant en A (ampère)
V = tension en V (volt)
R = résistance en W (ohm)
(Cette formule est tirée de la formule 74).
Exemple :
Données : V = 90 V ; R = 180 W
Intensité du courant : I = 90 / 180 = 0,5 A
OBSERVATION : la formule 76 peut aussi s'appliquer en exprimant la tension et la résistance respectivement avec les sous-multiples et multiples du volt et de l'Ohm. Par exemple, la tension peut être exprimée en millivolts (mV) et la résistance en ohm (W) : dans ce cas, l'intensité du courant sera exprimée en milliampères (mA) ; de même, la tension peut être exprimée en volts et la résistance en kilo-ohms (kW), l'intensité du courant sera exprimée en milliampères.
![]() FORMULE 77 - Calcul de la résistance totale
d'un circuit formé de plusieurs résistances reliées en série connaissant leurs valeurs.
FORMULE 77 - Calcul de la résistance totale
d'un circuit formé de plusieurs résistances reliées en série connaissant leurs valeurs.
Calculer la résistance totale d'un circuit formé de plusieurs résistances reliées en série
Énoncé : La valeur de la résistance équivalente à plusieurs résistances reliées en série est obtenue en faisant la somme des valeurs de chaque résistance.
Rt = R1 + R2 + Rn, etc..
Rt = résistance équivalente totale
R1 = valeur de la première résistance
R2 = valeur de la deuxième résistance
Rn = valeur de la dernière résistance
Les valeurs de résistance doivent toutes être exprimées dans la même unité de mesure (W, kW, MW).
-
Exemple :
a) Données : R1 = 300 W (ohm) ; R2 = 1 kW (kilo-ohm) = 1000 W
-
Résistance totale : Rt = 300 + 1000 = 1300 W
b) Données : R1 = 2 kW ; R2 = 0,5 kW ; R3 = 1500 W = 1,5 kW
-
Résistance totale : Rt = 2 + 0,5 + 1,5 = 4 kW
c) Données : R1 = 0,5 MW (mégohm ; 1 MW = 1 000 000 W) ; R2 = 2,7 MW ; R3 = 300 kW = 0,3 MW ; R4 = 1 MW
-
Résistance totale : Rt = 0,5 + 2,7 + 0,3 + 1 = 4,5 MW
![]() FORMULE 78 - Calcul
de la conductance totale d'un circuit formé de plusieurs résistances reliées
en parallèle connaissant leurs valeurs.
FORMULE 78 - Calcul
de la conductance totale d'un circuit formé de plusieurs résistances reliées
en parallèle connaissant leurs valeurs.
Calculer la conductance totale d'un circuit formé de plusieurs résistances reliées en parallèle
Énoncé : La conductance résultante de l'association de plusieurs résistances reliées en parallèle s'obtient en faisant la somme des conductances de chaque résistance, (voir théorie 2 dans la rubrique sommaire électronique).
Gt = G1 + G2 + ... + Gn
Gt = conductance totale
G1 = conductance de la première résistance
G2 = conductance de la deuxième résistance
Gn = conductance de la dernière résistance
Les valeurs des conductances doivent toutes être exprimées dans la même unité de mesure (S ou mS ou µS).
-
Exemple :
Données : G1 = 10 000 S ; G2 = 15 000 S ; G3 = 5 000 S ; G4 = 60 000 S
Conductance totale : Gt = 10 000 S + 15 000 S + 5 000 S + 60 000 S = 90 000 S
![]() FORMULE 79 - Calcul
de la résistance équivalente à plusieurs résistances reliées en parallèle
connaissant leurs valeurs.
FORMULE 79 - Calcul
de la résistance équivalente à plusieurs résistances reliées en parallèle
connaissant leurs valeurs.
Calculer la résistance équivalente (req) à 5 résistances reliées en parallèle
Calculer la résistance équivalente (req) à 4 résistances reliées en parallèle
Calculer la résistance équivalente (req) à 3 résistances reliées en parallèle
Calculer la résistance équivalente (req) à 2 résistances reliées en parallèle
Énoncé : La résistance équivalente à plusieurs résistances reliées en parallèle s'obtient en effectuant les calculs en trois temps : d'abord on calcule la conductance de chaque résistance (formule 70) ; puis on calcule la conductance totale des résistances en parallèle (formule 78) ; enfin, on calcule la résistance équivalente, c'est-à-dire la résistance qui correspond à la conductance totale (formule 71).
Tous les calculs indiqués dans l'énoncé précédent peuvent être traduits par la formule suivante :
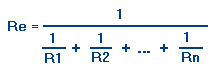
Re = résistance équivalente
R1 = valeur de la première résistance
R2 = valeur de la deuxième résistance
Rn = valeur de la dernière résistance
Les valeurs de résistance doivent toutes être exprimées dans la même unité de mesure (W, kW, MW).
-
Exemple :
Données : R1 = 200 W (ohm) ; R2 = 1 kW (kilo-ohm) = 1000 W ; R3 = 20 W ; R4 = 500 W ; R5 = 100 W
Résistance équivalente aux cinq résistances reliées en parallèle :
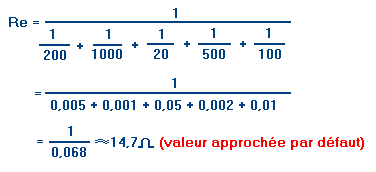
![]() FORMULE 80 - Calcul
de la résistance équivalente de deux résistances reliées en parallèle
connaissant leurs valeurs.
FORMULE 80 - Calcul
de la résistance équivalente de deux résistances reliées en parallèle
connaissant leurs valeurs.
Calculer la résistance équivalente de deux résistances reliées en parallèle
Énoncé : La résistance équivalente de deux résistances reliées en parallèle s'obtient en multipliant les valeurs des deux résistances et en divisant le tout par la somme de ces deux valeurs.
Re = (R1 x R2) / ( R1 + R2)
Re = résistance équivalente
R1 = valeur d'une résistance
R2 = valeur de l'autre résistance
Les valeurs de résistance doivent toutes être exprimées dans la même unité de mesure (W, kW, MW).
-
Exemple :
Données : R1 = 2 kW (kilo-ohm) = 2000 W ; R2 = 800 W
Résistance équivalente des deux résistances reliées en parallèle :
Re = (2 000 x 800) / (2 000 + 800) = 1 600 000 / 2 800 ![]() 571,4 W (valeur approchée par défaut).
571,4 W (valeur approchée par défaut).
OBSERVATION : Pour calculer la valeur de la résistance équivalente de deux résistances, on peut aussi se servir de la formule 79.
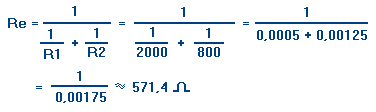
![]() FORMULE 81 -
Calcul de la valeur de la résistance
à mettre en parallèle avec une autre résistance de valeur connue pour obtenir une résistance équivalente donnée.
FORMULE 81 -
Calcul de la valeur de la résistance
à mettre en parallèle avec une autre résistance de valeur connue pour obtenir une résistance équivalente donnée.
Énoncé : La valeur de la résistance à mettre en parallèle avec une autre résistance de valeur connue pour obtenir une résistance équivalente donnée se calcule en multipliant la valeur de la résistance connue par la résistance équivalente, le tout divisé par la différence de ces deux valeurs.
Ri = (R x Re) / (R - Re)
Ri = résistance inconnue
R = valeur de la résistance disponible
Re = résistance équivalente que l'on veut obtenir
Les valeurs de résistance doivent toutes être exprimées dans la même unité de mesure (W, kW, MW).
-
Exemple :
Données : R = 2000 W (ohm) ; Re = 600 W
Résistance inconnue : Ri = (2 000 x 600) / (2 000 - 600) = 1 200 000 / 1 400 = 857 W (valeur approchée par défaut)
![]() FORMULE 82 -
Calcul de la résistance équivalente
à deux ou plusieurs résistances de même valeur reliées en parallèle.
FORMULE 82 -
Calcul de la résistance équivalente
à deux ou plusieurs résistances de même valeur reliées en parallèle.
Énoncé : La résistance équivalente de deux ou plusieurs résistances de valeurs égales reliées en parallèle s'obtient en divisant la valeur par le nombre de résistances.
Re = R / n
Re = résistance équivalente
R = valeur des résistances
n = nombre de résistances
La résistance équivalente sera exprimée dans la même unité de mesure que celle utilisée pour exprimer la valeur des résistances.
-
Exemple :
a) Données : R = 1 200 W (ohm) ; n = 2
-
Résistance équivalente : Re = 1 200 / 2 = 600 W
b) Données : R = 150 kW (kilo-ohm) ; n = 3
-
Résistance équivalente : Re = 150 / 3 = 50 kW
c) Données : R = 2 MW (mégohm) ; n = 4
-
Résistance équivalente : Re = 2 / 4 = 0,5 MW = 500 kW
![]() FORMULE 83 -
Calcul de la force électromotrice
(f.e.m.) obtenue en reliant en série deux
ou plusieurs piles, connaissant la force électromotrice de chaque pile.
FORMULE 83 -
Calcul de la force électromotrice
(f.e.m.) obtenue en reliant en série deux
ou plusieurs piles, connaissant la force électromotrice de chaque pile.
Calculer la force électromotrice (f.e.m.) obtenue en reliant en série deux ou plusieurs piles
Énoncé : En mettant en série deux ou plusieurs piles, on obtient une force électromotrice égale à la somme des forces électromotrices de chaque pile.
Et = E1 + E2 + ... + En
Et = force électromotrice totale
E1 = force électromotrice de la première pile
E2 = force électromotrice de la deuxième pile
En = force électromotrice de la dernière pile.
Les forces électromotrices doivent toutes être exprimées dans la même unité de mesure.
-
Exemple :
Données : E1 = 4,5 V (volt) ; E2 = 4,5 V ; E3 = 9 V ; E4 = En = 9 V
Force électromotrice totale : Et = 4,5 + 4,5 + 9 + 9 = 27 V.
![]() FORMULE 84 -
Calcul de la résistance interne
d'une pile connaissant sa f.e.m.
(tension à
vide lorsqu'elle ne fournit aucun courant) et la tension en charge lorsqu'elle fournit un courant donné.
FORMULE 84 -
Calcul de la résistance interne
d'une pile connaissant sa f.e.m.
(tension à
vide lorsqu'elle ne fournit aucun courant) et la tension en charge lorsqu'elle fournit un courant donné.
Calculer la résistance interne d'une pile connaissant sa force électromotrice
Énoncé : La résistance interne d'une pile est donnée par la différence entre la f.e.m. et la tension en charge, le tout divisé par le courant fourni.
Ri = (E - V) / I
Ri = résistance interne en W (ohm)
E = f.e.m. "tension à vide" en V (volt)
V = tension en charge en V (volt)
I = courant fournit en A (ampère).
-
Exemple :
Données : E = 4,5 V ; V = 4,2 V ; I = 0,3 A
Résistance interne : Ri = (4,5 - 4,2) / 0,3 = 0,3 / 0,3 = 1 W
![]() FORMULE 85 - Calcul
de la puissance électrique d'un appareil connaissant la tension appliquée et l'intensité du courant absorbé.
FORMULE 85 - Calcul
de la puissance électrique d'un appareil connaissant la tension appliquée et l'intensité du courant absorbé.
Calculer la puissance électrique d'un appareil
Énoncé : La puissance électrique, exprimée en watts, s'obtient en multipliant la tension, exprimée en volts, par l'intensité du courant exprimée en ampères.
P = VI
P = puissance électrique en W (watt)
V = tension en V (volt)
I = intensité du courant en A (ampère)
-
Exemple :
Données : V = 200 V ; I = 1,5 A
Puissance : P = 200 x 1,5 = 300 W
![]() FORMULE 86 -
Calcul de l'intensité du courant
absorbé par un appareil connaissant la tension appliquée et sa puissance électrique.
FORMULE 86 -
Calcul de l'intensité du courant
absorbé par un appareil connaissant la tension appliquée et sa puissance électrique.
Calculer l'intensité du courant absorbé par un appareil
I = P / V
I = intensité du courant absorbé en A (ampère)
P = puissance électrique en W (watt)
V = tension appliquée en V (volt)
(Cette formule est tirée de la formule 85)
-
Exemple :
Données : P = 300 W ; V = 220 V
Intensité du courant : I = 300 / 220 = 1,36 A (valeur approchée par défaut).
![]() FORMULE 87 - Calcul
de la tension appliquée à un appareil connaissant l'intensité du courant absorbé et la puissance électrique de celui-ci.
FORMULE 87 - Calcul
de la tension appliquée à un appareil connaissant l'intensité du courant absorbé et la puissance électrique de celui-ci.
Calculer la tension appliquée à un appareil
V = P / I
V = tension appliquée en V (volt)
P = puissance électrique en W (watt)
I = intensité du courant absorbé en A (ampère).
(Cette formule est tirée de la formule 85).
-
Exemple :
Données : P = 1 200 W ; I = 5,455 A
Tension appliquée : V = 1 200 / 5,455 = 220 V (valeur approchée)
![]() FORMULE 88 -
Calcul de l'énergie électrique consommée
par un appareil connaissant sa puissance électrique et sa durée de fonctionnement.
FORMULE 88 -
Calcul de l'énergie électrique consommée
par un appareil connaissant sa puissance électrique et sa durée de fonctionnement.
Calculer l'énergie électrique consommée par un appareil
Énoncé : L'énergie consommée par un appareil, exprimée en watts-secondes, s'obtient en multipliant la puissance de l'appareil, exprimée en watts, par le temps de fonctionnement exprimé en secondes.
W = Pt
W = énergie consommée en W.s (watt-seconde)
P = puissance électrique en W (watt)
t = temps en s (secondes)
-
Exemple :
Données : P = 600 W ; t = 5 mn (minutes) = 300 s
Énergie consommée : W = 600 x 300 = 180 000 W.s
OBSERVATION : Le watt-seconde (W.s), unité de mesure utilisée pour exprimer la quantité d'énergie électrique consommée, est équivalent à 1 joule (J), unité de mesure de l'énergie et du travail mécanique.
1 W.s = 1 J
En pratique, pour indiquer la consommation domestique et industrielle de l'énergie électrique, on utilise un multiple du watt-seconde, c'est-à-dire le kilowatt-heure (kW.h).
1 kW.h = 3 600 000 W.s ; 1 W.s = 1 / 3 600 000 kW.h
Le résultat de l'exemple précédent peut s'exprimer en kW.h au moyen de l'équivalence :
180 000 W.s = 180 000 / 3 600 000 kW.h = 0,05 kW.h
Si dans la formule 88, la puissance est exprimée en kilowatts (kW ; 1 kW = 1000 W) et le temps en heures (h, 1 h = 60 mn = 3 600 s), l'énergie consommée sera exprimée en kilowatts-heures.
Par exemple, si P = 800 W = 0,8 kW et "t" = 30 mn = 0,5 h, l'énergie consommée sera de :
W = 0,8 x 0,5 = 0,4 kW.h
![]() FORMULE 89 -
Calcul de la puissance électrique
dissipée par effet Joule dans une résistance connaissant l'intensité du
courant et la valeur de cette résistance.
FORMULE 89 -
Calcul de la puissance électrique
dissipée par effet Joule dans une résistance connaissant l'intensité du
courant et la valeur de cette résistance.
Calculer la puissance électrique dissipée par effet Joule dans une résistance
Énoncé : La puissance électrique, exprimée en watts, dissipée dans une résistance s'obtient en multipliant la résistance, exprimée en ohms, par le carré du courant qui la traverse, exprimé en ampères.
P = RI2
P = puissance électrique en W (watt)
R = résistance en W (ohm)
I = intensité du courant en A (ampère)
-
Exemple :
Données : R = 125 W ; I = 0,3 A
Puissance électrique dissipée : P = 125 x 0,32 = 125 x 0,09 = 11,25 W
![]() FORMULE 90 - Calcul
de la valeur d'une résistance connaissant la puissance électrique dissipée et l'intensité du courant qui la traverse.
FORMULE 90 - Calcul
de la valeur d'une résistance connaissant la puissance électrique dissipée et l'intensité du courant qui la traverse.
R = P / I2
R = résistance en W (ohm)
P = puissance dissipée en W (watt)
I = intensité du courant en A (ampère)
(Cette formule est tirée de la formule 89)
-
Exemple :
Données : P = 100 W ; I = 0,5 A
Résistance : R = 100 / 0,52 = 100 / 0,25 = 400 W
![]() FORMULE 91- Calcul
de l'intensité du courant qui parcourt une résistance connaissant la puissance électrique dissipée et la valeur de cette résistance.
FORMULE 91- Calcul
de l'intensité du courant qui parcourt une résistance connaissant la puissance électrique dissipée et la valeur de cette résistance.
Calculer l'intensité du courant qui parcourt une résistance.
Énoncé : L'intensité du courant, exprimée en ampères, qui parcourt une résistance, s'obtient en divisant la puissance dissipée exprimée en watts par la résistance exprimée en ohms, et en extrayant la racine carrée du quotient obtenu.

![]() FORMULE 92 - Calcul
de la puissance électrique dissipée par effet Joule dans une résistance connaissant la tension appliquée et la valeur de cette résistance.
FORMULE 92 - Calcul
de la puissance électrique dissipée par effet Joule dans une résistance connaissant la tension appliquée et la valeur de cette résistance.
Calculer la puissance électrique dissipée par effet Joule dans une résistance.
Énoncé : La puissance électrique, exprimée en watts, dissipée dans une résistance s'obtient en divisant le carré de la tension, exprimée en volts, par la résistance exprimée en ohms.
P = V2 / R
P = puissance électrique en W (watt)
V = tension en V (volt)
R = résistance en W (ohm)
-
Exemple :
Données : V = 220 V ; R = 242 W
Puissance électrique dissipée : P = 2202 / 242 = 48 400 / 242 = 200 W
![]() FORMULE 93 -
Calcul de la valeur d'une résistance connaissant la puissance électrique dissipée et la tension appliquée.
FORMULE 93 -
Calcul de la valeur d'une résistance connaissant la puissance électrique dissipée et la tension appliquée.
R = V2 / P
R = résistance en W (ohm)
V = tension appliquée en V (volt)
P = puissance électrique dissipée en W (watt)
(Cette formule est tirée de la formule 92).
-
Exemple :
Données : 220 V ; P = 400 W
Résistance : R = 2202 / 400 = 48 400 / 400 = 121 W
![]() FORMULE 94 - Calcul
de la tension appliquée à une résistance connaissant la puissance électrique dissipée et la valeur de cette résistance.
FORMULE 94 - Calcul
de la tension appliquée à une résistance connaissant la puissance électrique dissipée et la valeur de cette résistance.
Énoncé : La tension appliquée à une résistance, exprimée en volts, s'obtient en multipliant la puissance dissipée exprimée en watts, par la résistance exprimée en ohms et en extrayant la racine carrée du produit obtenu.
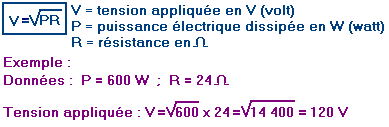
![]() FORMULE 95 - Calcul
de la quantité de chaleur obtenue en transformant par effet Joule une quantité
d'énergie électrique donnée (pour le calcul de l'énergie électrique, voir la formule 88).
FORMULE 95 - Calcul
de la quantité de chaleur obtenue en transformant par effet Joule une quantité
d'énergie électrique donnée (pour le calcul de l'énergie électrique, voir la formule 88).
Énoncé : La quantité de chaleur exprimée en kilo-calories produite dans une résistance par effet Joule s'obtient en multipliant l'énergie électrique exprimée en watts-secondes (Joule) dissipée dans cette résistance par le nombre 0,000238.
Qc = 0,000238 W (Valeur approchée par défaut)
Qc = quantité de chaleur en kilo-calories
W = énergie électrique en W.s (watt-seconde) ou bien en J (Joule)
-
Exemple :
Données : Énergie électrique dissipée par une résistance W = 0,5 kW.h (kilowatt-heure) = 3 600 000 x 0,5 = 1 800 000 W.s (pour l'équivalence entre le kilowatt-heure et le watt-seconde, voir l'observation qui suit la formule 88).
Quantité de chaleur produite par la résistance : Qc = 0,000 238 x 1 800 000 = 428,4 kcal.
![]() FORMULE 96 -
Calcul de la résistance à chaud d'un conducteur connaissant
l'augmentation de température du matériau et la résistance du conducteur à la température ambiante (20° C).
FORMULE 96 -
Calcul de la résistance à chaud d'un conducteur connaissant
l'augmentation de température du matériau et la résistance du conducteur à la température ambiante (20° C).
Calculer la résistance à chaud d'un conducteur
Énoncé : En augmentant la température d'un conducteur, on augmente sa résistance électrique. Pour le calcul de la résistance à chaud d'un conducteur, il faut compléter l'énoncé de la façon suivante : la résistance à chaud, exprimée en ohms, s'obtient en additionnant la résistance du conducteur à la température ambiante (20° C) avec le produit du coefficient de température du matériau, de la résistance à la température ambiante et de l'augmentation de température exprimée en degrés Celsius.
Les coefficients de température des principaux matériaux conducteurs sont reportés dans la dernière colonne de droite du tableau III (nous reportons la même figure 1 ci-dessous).
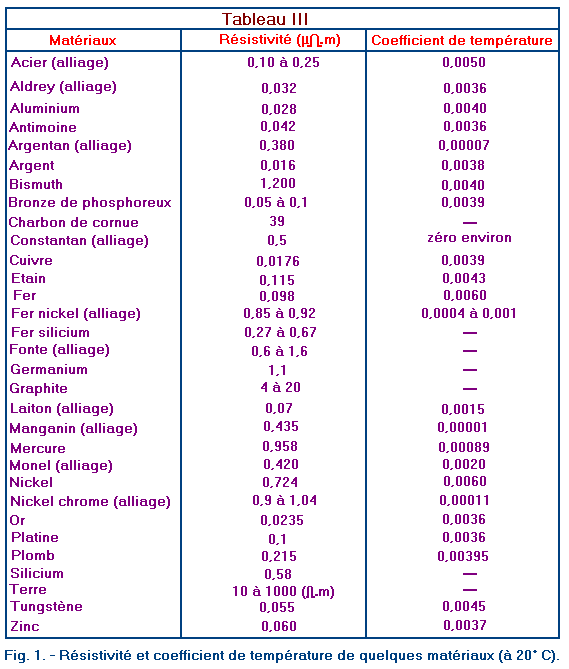
Rt = résistance à chaud (à la température t) en W (ohm)
R20 = résistance à froid (à la température de 20° C) en W (ohm)
![]() =
coefficient de température du matériau
=
coefficient de température du matériau
t = température du conducteur chaud en °C (degrés Celsius)
t - 20 = augmentation de température en °C (degrés Celsius)
-
Exemple :
Données relatives à un
conducteur de tungstène : R20 = 30 W (résistance à froid du conducteur) ; ![]() = 0,0045 (coefficient de température du tungstène) ; t = 320° C (température du conducteur).
= 0,0045 (coefficient de température du tungstène) ; t = 320° C (température du conducteur).
Augmentation de température du conducteur : t - 20 = 320 - 20 = 300° C
Résistance à chaud du conducteur : Rt = 30 + 0,0045 x 30 x 300 = 30 + 40,5 = 70,5 W
![]() FORMULE 97 -
Calcul de la résistance par mètre à froid (à 20° C) d'un conducteur connaissant sa section et la résistivité du matériau.
FORMULE 97 -
Calcul de la résistance par mètre à froid (à 20° C) d'un conducteur connaissant sa section et la résistivité du matériau.
Calculer la résistance par mètre à froid (à 20° C) d'un conducteur
(R / m) = (p / S)
R / m = résistance par mètre en W / m (ohm par mètre)
p = résistivité en µW.m (microhm-mètre)
S = section en mm2
* Cette formule est tirée de la formule 64 ("voir formulaire mathématiques 2 - 1ère partie") en donnant à la longueur du conducteur la valeur de 1 mètre *.
-
Exemple :
Données relatives à un conducteur de nickel-chrome : p = 0,9 µW.m (résistivité du nickel-chrome à température de 20° C ; tableau III, figure 1) ; S = 0,007854 mm2 (section du conducteur).
Résistance par mètre (à 20° C) : R / m = 0,9 / 0,007854 = 115 W / m (valeur approchée)
OBSERVATION : Dans le tableau IV ("voir le formulaire mathématique 2, 1ère partie, figure 2"), on a reporté les valeurs de résistance par mètre des conducteurs de nickel-chrome, constantan et manganin pour les sections d'usage le plus fréquent dans les applications électriques.
![]() FORMULE 98 - Calcul de la résistance par mètre à chaud d'un fil de chauffage connaissant la résistance par mètre à froid
(formule 97), le coefficient de température du matériau (tableau III, figure 1) et la température de fonctionnement du fil de chauffage.
FORMULE 98 - Calcul de la résistance par mètre à chaud d'un fil de chauffage connaissant la résistance par mètre à froid
(formule 97), le coefficient de température du matériau (tableau III, figure 1) et la température de fonctionnement du fil de chauffage.
(R / m)t = (R / m)20 + ![]() (R
/ m)20 (t - 20)
(R
/ m)20 (t - 20)
(R / m) t = résistance par mètre à la température de fonctionnement du fil de chauffage en W / m (ohm par mètre).
(R / m)20 = résistance par mètre à la température ambiante en W / m (ohm par mètre)
![]() = coefficient de température du matériau
= coefficient de température du matériau
t = température de fonctionnement du fil de chauffage en ° C (degrés Celsius)
t - 20 = augmentation de température en ° C (degrés Celsius)
(Cette formule est tirée de la formule 96 en substituant le symbole de la résistance (R) à celui de la résistance par mètre, R / m).
-
Exemple :
Données :
(R / m) 20 = 5,65
W
/ m (résistance
par mètre à froid d'un fil de nickel-chrome ayant un diamètre de 0,45
mm ; tableau IV, figure 2) ;
![]() = 0,00011 (coefficient de température du nickel-chrome ;
tableau III, figure 1) ; t = 1020° C (température de fonctionnement du fil de chauffage).
= 0,00011 (coefficient de température du nickel-chrome ;
tableau III, figure 1) ; t = 1020° C (température de fonctionnement du fil de chauffage).
Augmentation de température pendant le passage de la température ambiante à la température de fonctionnement du fil : t - 20 = 1020 - 20 = 1000° C
Résistance par mètre
à 1020° C : (R / m)t = 5,65 + 0,00011 x 5,65 x 1000 = 5,65 + 0,6215 = 6,2715 ![]() 6,28 W / m (valeur approchée par excès).
6,28 W / m (valeur approchée par excès).
OBSERVATION : Le calcul de la résistance par mètre à chaud d'un fil de chauffage est nécessaire pour en déterminer la longueur quand on connaît la valeur de la résistance qu'il doit avoir pendant le fonctionnement, c'est-à-dire sa résistance à chaud. Pour mieux expliquer avec un exemple pratique, voyons comment on doit procéder dans le calcul de la résistance au nickel-chrome d'un appareil de chauffage électrique.
Calcul de la résistance d'un appareil de chauffage (four électrique, étuve électrique, etc...).
Données : Le four est alimenté avec la tension de 220 V et doit dissiper une puissance de 600 W à la température d'environ 1020° C (température de fonctionnement du fil de chauffage).
Procédé :
1) On calcule l'intensité du courant qui alimente le four dans les conditions normales de fonctionnement ; dans ce but, on utilise la formule 86 :
I = P / V = 600 / 220 = ![]() 2,73 A (valeur approchée par excès)
2,73 A (valeur approchée par excès)
2) En se basant sur la valeur du courant calculé, on choisit la section du fil ; pour le courant de 2,73 A, il faudra choisir un fil de nickel-chrome de diamètre 0,45 mm correspondant à la section de 0,159043 mm2 (voir tableau 4 de la figure 2, 1ère théorie). D'une façon générale, pour faire ce choix, il faut connaître la densité de courant nécessaire pour maintenir le fil de nickel-chrome à la température de fonctionnement.
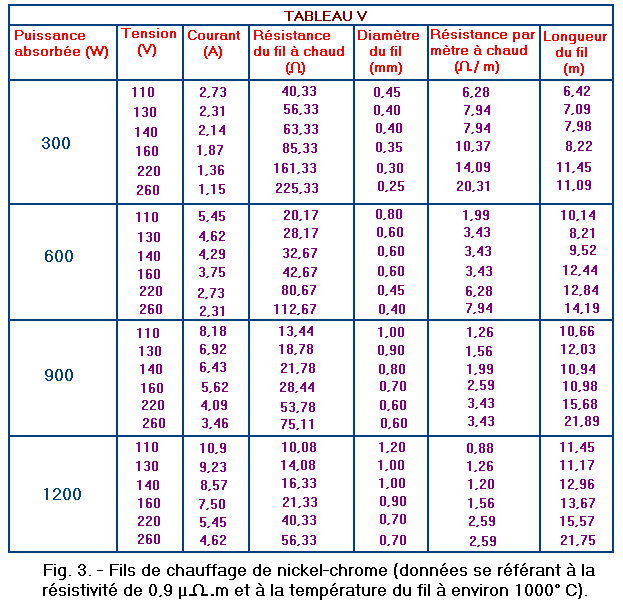
Par la suite, dans le formulaire 4, nous verrons comment procéder pour calculer la section d'un fil conducteur connaissant la densité de courant admise par le matériau et l'intensité du courant qui doit passer dans le fil ; il vous suffit de connaître maintenant les diamètres des fils qui sont indiqués dans la cinquième colonne en partant de la gauche sur le tableau V (figure 3 ci-dessous) en correspondance avec les diverses valeurs du courant reportées dans la troisième colonne.
3) On calcule la valeur de la résistance à chaud que le fil doit présenter pour dissiper la puissance de 600 W, la tension de 220 V étant appliquée ; on utilise dans ce but la formule 93 :
R = V2 / P = 2202
/ 600 = 48 400 / 600 = 80,666 ![]() 80,67 W
(valeur approchée par excès)
80,67 W
(valeur approchée par excès)
4) En consultant le tableau IV (figure 2, formulaire mathématique 2, 1ère partie), on détermine la résistance par mètre à froid du fil de nickel-chrome ayant un diamètre de 0,45 mm (section de 0,159043 mm2) ; la valeur indiquée sur le tableau est de 5,65 W / m.
5) Connaissant la valeur de la résistance par mètre à froid du fil nickel-chrome choisi, on calcule la valeur de la résistance par mètre de ce même fil à la température de fonctionnement (1020° C) ; dans ce but, on utilise la formule 98 :
(R / m) t = (R / m)20 + ![]() (R
/ m)20 (t - 20)
(R
/ m)20 (t - 20)
= 5,65 + 0,00011 x 5,65 x 1000
= 5,65 + 0,6215 = 6,2715 ![]() 6,28 W / m (valeur approchée par excès)
6,28 W / m (valeur approchée par excès)
On peut éviter ce calcul en reprenant la valeur de la résistance par mètre à chaud dans le tableau V (figure 3) en correspondance avec les valeurs de 600 W et 220 V.
6) Connaissant la valeur de la résistance à chaud du fil (80,67 W) et la valeur de la résistance par mètre à chaud (6,28 W), on calcule la longueur du fil en divisant la première valeur par la seconde :
80,67 / 6,28 = 12,84 mètres
Pour construire un four électrique fonctionnant avec la tension de 220 V, à la température d'environ 1000° C (1020° C dans les calculs) de façon à dissiper une puissance de 600 W, on peut donc utiliser un fil de nickel-chrome ayant la résistivité de 0,9 µW.m (tableau III, figure 1).
La valeur de la résistivité du nickel-chrome n'a pas été mentionnée dans le calcul, mais a été introduite précédemment dans la formule 97 pour calculer les résistances par mètre indiquées dans le tableau IV (figure 2, "1ère partie du formulaire mathématiques N° 2"), c'est-à-dire les valeurs des résistances par mètre à froid utilisées successivement dans la formule 98 pour calculer les résistances par mètre à chaud indiquées dans le tableau V (ci-dessus).
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet.
|
|
 Page précédente Page précédente
|
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Calcul de la résistance d'un circuit
Calcul de la résistance d'un circuit