Formulaire 1. 4. - Électromagnétisme :
Dans ce dernier formulaire, vous trouverez la suite des formules concernant l'électromagnétisme et les diverses grandeurs relatives aux signaux périodiques les plus couramment utilisés en électronique.
![]() FORMULE 124
Calcul de la force magnétomotrice
produite par une bobine parcourue par un courant, connaissant le nombre de spires de l'enroulement et l'intensité du courant.
FORMULE 124
Calcul de la force magnétomotrice
produite par une bobine parcourue par un courant, connaissant le nombre de spires de l'enroulement et l'intensité du courant.
Calcul de la force magnétomotrice produite par une bobine parcourue par un courant
Énoncé : La force magnétomotrice, exprimée en ampères-tours, s'obtient en multipliant le nombre de spires par l'intensité du courant, exprimée en ampères.
F = NI
F = force magnétomotrice en A.t (ampère-tour)
N = nombre de spires
I = intensité du courant en A (ampère)
Exemple :
Données : N = 1 600 (nombre de spires d'une bobine) ; I = 0,05 A (intensité du courant qui parcourt l'enroulement de la bobine).
Force magnétomotrice produite par la bobine : F = 1 600 x 0,05 = 80 A.t.
![]() FORMULE 125
-
Calcul du nombre de spires d'une bobine, connaissant la force magnétomotrice qu'elle doit produire et l'intensité du courant qui parcourt l'enroulement.
FORMULE 125
-
Calcul du nombre de spires d'une bobine, connaissant la force magnétomotrice qu'elle doit produire et l'intensité du courant qui parcourt l'enroulement.
Calcul du nombre de spires d'une bobine
N = F / I
N = nombre de spires de l'inducteur
F = force magnétomotrice en A.t (ampère-tour)
I = intensité du courant en A (ampère)
(Cette formule est tirée de la formule 124).
Exemple :
Données : F = 100 A.t ; I = 0,025 A
Nombre de spires de l'enroulement : N = 100 / 0,025 = 4 000.
![]() FORMULE 126 - Calcul de l'intensité du
courant qui doit parcourir l'enroulement d'une bobine, connaissant la force magnétomotrice
de la bobine et le nombre de spires de l'enroulement.
FORMULE 126 - Calcul de l'intensité du
courant qui doit parcourir l'enroulement d'une bobine, connaissant la force magnétomotrice
de la bobine et le nombre de spires de l'enroulement.
Calcul de l'intensité du courant qui doit parcourir l'enroulement d'une bobine
I = F / N
I = intensité du courant en A (ampère)
F = force magnétomotrice en A.t (ampère-tour)
N = nombre de spires de la bobine
(Cette formule est tirée de la formule 124).
Exemple :
Données : F = 50 A.t. ; N = 800
Intensité du courant qui parcourt l'enroulement de la bobine :
I = 50 / 800 = 0,0625 A
![]() FORMULE 127
- Calcul de la perméabilité magnétique absolue d'un matériau, connaissant la perméabilité
absolue du vide et la perméabilité relative du matériau.
FORMULE 127
- Calcul de la perméabilité magnétique absolue d'un matériau, connaissant la perméabilité
absolue du vide et la perméabilité relative du matériau.
Calcul de la perméabilité magnétique absolue d'un matériau
Énoncé : La perméabilité magnétique absolue d'un matériau, exprimée en micro-henrys par mètre, s'obtient en multipliant la perméabilité magnétique absolue du vide, exprimée en micro-henrys par mètre, par la perméabilité relative du matériau.
µ = µo x µr
µ = perméabilité magnétique absolue du matériau en µH / m (micro-henry par mètre)
µo = perméabilité magnétique absolue du vide égale à 1,256 µH / m (micro-henry par mètre)
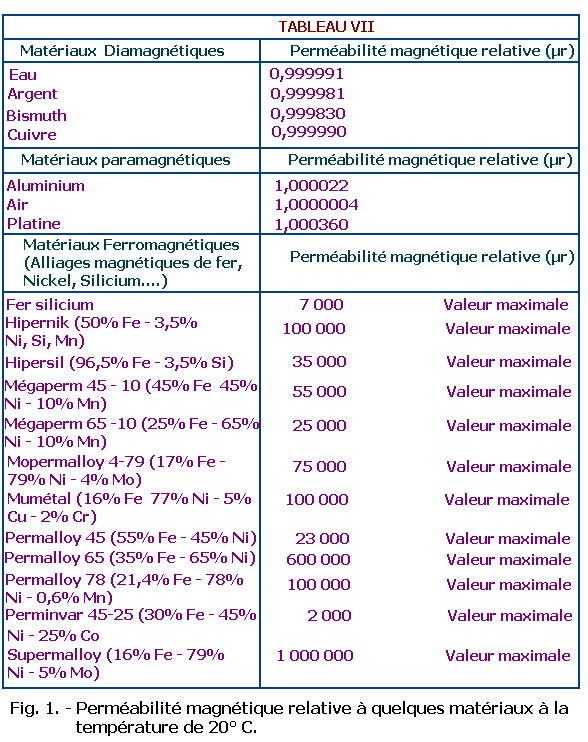
µr = perméabilité magnétique relative du matériau (tableau VII, figure 1).
-
Exemple :
Données : µo = 1,256 µH / m ; µr = 2 000 (valeur maximale de la perméabilité relative de l'alliage magnétique perminvar 45 - 25 (valeur maximale) :
µ = 1,256 x 2 000 = 2 512 µH / m.
Au tableau VII de la figure 1, on a donné les valeurs de la perméabilité magnétique relative à quelques matériaux diamagnétiques, paramagnétiques et ferromagnétiques. On notera qu'en général, les matériaux diamagnétiques ont une valeur de perméabilité relative légèrement inférieures à 1 et que les matériaux paramagnétiques ont des valeurs de perméabilité relative légèrement supérieures à 1 ; ces valeurs peuvent se considérer comme pratiquement égales à 1 dans toutes les applications techniques.
La perméabilité absolue des matériaux diamagnétiques et paramagnétiques est donc pratiquement égale à celle du vide.
µ = µo x µr = 1,256 x 1 = 1,256 µH / m
La perméabilité des matériaux ferromagnétiques n'est pas constante mais change selon la variation de l'intensité de magnétisation ; pour cette raison, on a indiqué au tableau VII les valeurs maximales. Ces valeurs ne suffisent pourtant pas à caractériser le comportement des matériaux ferromagnétiques ; dans ce but, il faudrait fournir des graphiques particuliers, appelés courbes de magnétisation ; par ces graphiques (qui présentent peu d'intérêt pour l'électronicien et qui ne seront donc pas pris en considération dans le formulaire), on peut établir la valeur de la perméabilité absolue des matériaux ferromagnétiques en relation avec les diverses valeurs de l'intensité de magnétisation de ces mêmes matériaux.
![]() FORMULE 128 -
Calcul de la perméabilité magnétique relative d'un matériau, connaissant
la perméabilité absolue du vide et du matériau.
FORMULE 128 -
Calcul de la perméabilité magnétique relative d'un matériau, connaissant
la perméabilité absolue du vide et du matériau.
Calcul de la perméabilité magnétique relative d'un matériau
µr = µ / µo
µr = perméabilité magnétique relative
µ = perméabilité absolue du matériau en µH / m (microhenry par mètre)
µo = perméabilité absolue du vide = 1,256 µH / m (microhenry par mètre)
(Cette formule est tirée de la formule 127).
-
Exemple :
Données : µ = 8 792 µH / m (perméabilité magnétique absolue du fer silicium) ; µo = 1,256 µH / m
Perméabilité relative du fer silicium : µr = 8 792 / 1,256 = 7 000
(Voir tableau VII, figure 1).
![]() FORMULE 129 -
Calcul de l'inductance d'une bobine à une seule couche, sans noyau, connaissant la perméabilité absolue de l'air, la section des spires, le nombre
de spires et la longueur de la bobine.
FORMULE 129 -
Calcul de l'inductance d'une bobine à une seule couche, sans noyau, connaissant la perméabilité absolue de l'air, la section des spires, le nombre
de spires et la longueur de la bobine.
Calcul de l'inductance d'une bobine à une seule couche
Énoncé : L'inductance d'une bobine à une seule couche, sans noyau, exprimée en microhenrys, s'obtient en multipliant la perméabilité absolue de l'air, exprimée en microhenrys par mètre, par la section des spires, exprimée en centimètres carrés, par le carré du nombre de spires et en divisant le produit obtenu par la longueur de la bobine, exprimée en centimètres et multipliée par 100.
L = µSN2 / 100 l
L = inductance en µH (microhenry)
µ = perméabilité absolue de l'air en µH / m (microhenry par mètre)
S = section des spires en cm2
N = nombre de spires
l = longueur de la bobine en cm.
-
Exemple :
Données
: µ ![]() 1,256 µH / m (valeur de la perméabilité absolue de l'air ;
l'air est une substance paramagnétique ; voir à
ce propos le tableau VII, figure 1 et l'observation
qui suit la formule 127) ; S = 7,068 cm2
(section d'une bobine cylindrique à spires jointives de 3
cm de diamètre ; pour le calcul de la section, connaissant le
diamètre, voir la formule 19 du formulaire) ; N = 120 spires ;
l = 3,6 cm (longueur de la bobine).
1,256 µH / m (valeur de la perméabilité absolue de l'air ;
l'air est une substance paramagnétique ; voir à
ce propos le tableau VII, figure 1 et l'observation
qui suit la formule 127) ; S = 7,068 cm2
(section d'une bobine cylindrique à spires jointives de 3
cm de diamètre ; pour le calcul de la section, connaissant le
diamètre, voir la formule 19 du formulaire) ; N = 120 spires ;
l = 3,6 cm (longueur de la bobine).
Inductance de la bobine :
L = (1,256 x 7,068 x 1202) / (100 x 3,6) = (1,256 x 7,068 x 14 400) / (100 x 3,6)
L ![]() 127 834 / 360
127 834 / 360 ![]() 355 µH
355 µH
OBSERVATION :
La formule 129 pour le calcul de l'inductance est valable en théorie, quand on admet que tout le flux magnétique produit par le courant est embrassé par les spires de l'enroulement ; en pratique, il arrive pourtant qu'une partie du flux magnétique produit soit dispersé ; pour tenir compte du flux dispersé, on a recours à des formules empiriques pour les calculs de projets.
![]() FORMULE 130 - Calcul
du flux embrassé par les spires d'un enroulement, connaissant l'inductance et l'intensité du courant.
FORMULE 130 - Calcul
du flux embrassé par les spires d'un enroulement, connaissant l'inductance et l'intensité du courant.
Calcul du flux embrassé par les spires d'un enroulement
Énoncé : Le flux embrassé par les spires d'un enroulement, exprimé en webers, s'obtient en multipliant l'inductance, exprimée en henrys, par l'intensité du courant qui parcourt l'enroulement, exprimée en ampères.
Fc = LI
Fc = flux embrassé par les spires d'un enroulement en Wb (weber)
L = inductance en H (henry)
I = intensité du courant en A (ampère)
-
Exemple :
Données : L = 2,5 H ; I = 0,03 A.
Flux embrassé par les spires de l'enroulement : Fc = 2,5 x 0,03 = 0,075 Wb.
OBSERVATION :
La formule 130 se réfère à un inducteur idéal, c'est-à-dire à une bobine dans laquelle tout le flux magnétique produit par le courant est embrassé par les spires de l'enroulement.
![]() FORMULE 131 - Calcul
de l'inductance d'une bobine, connaissant le flux embrassé par les spires de l'enroulement et l'intensité du courant qui le parcourt.
FORMULE 131 - Calcul
de l'inductance d'une bobine, connaissant le flux embrassé par les spires de l'enroulement et l'intensité du courant qui le parcourt.
Calcul de l'inductance d'une bobine
L = Fc / I
L = inductance en H (henry)
Fc = flux embrassé en Wb (weber)
I = intensité du courant en A (ampère)
(Cette formule est tirée de la formule 130).
-
Exemple :
Données : Fc = 0,002 / 0,05 = 0,04 H
![]() FORMULE 132 - Calcul de l'intensité du
courant qui parcourt une bobine, connaissant l'inductance et le flux embrassé par les spires de l'enroulement.
FORMULE 132 - Calcul de l'intensité du
courant qui parcourt une bobine, connaissant l'inductance et le flux embrassé par les spires de l'enroulement.
Calcul de l'intensité du courant qui parcourt une bobine
I = Fc / L
(Cette formule est tirée de la formule 130).
-
Exemple :
Données : Fc = 0,6 Wb ; L = 250 mH (millihenry) = 0,25 H.
Intensité du courant : I = 0,6 / 0,25 = 2,4 A.
![]() FORMULE 133 - (loi de NEUMANN). Calcul de la
force électromotrice induite dans une spire, connaissant la variation du flux
magnétique embrassé par la spire et le temps pendant lequel s'accomplit cette variation.
FORMULE 133 - (loi de NEUMANN). Calcul de la
force électromotrice induite dans une spire, connaissant la variation du flux
magnétique embrassé par la spire et le temps pendant lequel s'accomplit cette variation.
Calcul de la force électromotrice induite dans une spire
Énoncé : La force électromotrice induite, exprimée en volts, s'obtient en divisant la variation du flux embrassé exprimée en webers, par le temps pendant lequel se produit cette variation, exprimée en secondes.
E = (F"c - F'c) / (t" - t')
E = force électromotrice induite en V (volt)
F"c = valeur du flux embrassé à la fin de l'intervalle considéré
F'c = valeur du flux embrassé au début de l'intervalle considéré
F"c - F'c = variation du flux en Wb (weber) qui s'écrit souvent ![]() Fc
Fc
t" = instant final
t' = instant initial
t" - t' = intervalle de temps en secondes qui s'écrit souvent ![]() t
t
La formule s'écrit également :
E = ![]() Fc
/
Fc
/ ![]() t
t
-
Exemple :
Données :
F"c - F'c = ![]() Fc
= 2,2 Wb ; t" - t' =
Fc
= 2,2 Wb ; t" - t' = ![]() t
= 0,02 s.
t
= 0,02 s.
Force électromotrice induite : E = 2,2 / 0,02 = 110 V
![]() FORMULE 134 - Calcul de la force électromotrice
d'auto-induction, connaissant l'inductance de l'enroulement, la variation de
l'intensité du courant qui le parcourt et le temps pendant lequel se produit cette variation.
FORMULE 134 - Calcul de la force électromotrice
d'auto-induction, connaissant l'inductance de l'enroulement, la variation de
l'intensité du courant qui le parcourt et le temps pendant lequel se produit cette variation.
Calcul de la force électromotrice d'auto-induction
Énoncé : La force électromotrice d'auto-induction, exprimée en volts, s'obtient en multipliant l'inductance, exprimée en henrys, par la variation de l'intensité du courant, exprimée en ampères et en divisant le produit obtenu par le temps durant lequel se produit cette variation exprimé en secondes.
E = L x (I" - I') / (t" - t') = L![]() I
/
I
/ ![]() t
t
E = force électromotrice d'auto-induction en V (volt)
L = inductance en H (henry)
I" = intensité finale du courant
I' = intensité initiale du courant
I" - I' = variation de l'intensité du courant en A (ampère) qui s'écrit souvent ![]() I
I
t" = instant final
t' = instant initial
t" - t' = intervalle de temps en secondes qui s'écrit souvent ![]() t
t
-
Exemple :
Données :
L = 2,5 H
(inductance d'un enroulement avec
noyau) ; ![]() I
= 0,6 A ;
I
= 0,6 A ; ![]() t = 0,01 s.
t = 0,01 s.
Force électromotrice d'auto-induction :
E = (2,5 x 0,6) / 0,01 = 1,5 / 0,01 = 150 V
![]() FORMULE 135 - Calcul
de l'inductance d'un enroulement, connaissant la force électromotrice d'auto-induction, la variation de l'intensité du courant et le temps pendant
lequel se produit cette variation.
FORMULE 135 - Calcul
de l'inductance d'un enroulement, connaissant la force électromotrice d'auto-induction, la variation de l'intensité du courant et le temps pendant
lequel se produit cette variation.
Calcul de l'inductance d'un enroulement
L = E x (t" - t') / (I" - I') = E![]() t
/
t
/ ![]() I
I
L = inductance en H (henry)
E = force électromotrice d'auto-induction en V (volt)
t" = instant final
t' = instant initial
t" - t' = ![]() t
= intervalle de temps en secondes
t
= intervalle de temps en secondes
I" = intensité finale du courant
I' = intensité initiale du courant
I" - I' = ![]() I
= variation de l'intensité du courant en A (ampère)
I
= variation de l'intensité du courant en A (ampère)
(Cette formule est tirée de la formule 134)
-
Exemple :
Données :
E = 120 V ; ![]() t
= 0,01 s ;
t
= 0,01 s ; ![]() I = 0,8 A.
I = 0,8 A.
Inductance de l'enroulement : L = (120 x 0,01) / 0,8 = 1,2 / 0,8 = 1,5 H
![]() FORMULE 136 - Calcul de l'inductance totale
présentée par deux ou plusieurs bobines reliées en série et non couplées
entre elles, connaissant l'inductance de chacune des bobines.
FORMULE 136 - Calcul de l'inductance totale
présentée par deux ou plusieurs bobines reliées en série et non couplées
entre elles, connaissant l'inductance de chacune des bobines.
Énoncé : L'inductance présentée en même temps par deux ou plusieurs bobines reliées en série s'obtient en additionnant les inductances des bobines.
Lt = L1 + L2 + L3 + ... + Ln
Lt = inductance totale
L1 = inductance de la première bobine
L2 = inductance de la seconde bobine
L3 = inductance de la troisième bobine
Ln = inductance de la dernière bobine
Les diverses inductances doivent toutes être exprimées dans la même unité de mesure.
-
Exemples :
a) Données : L1 = 0,5 H (henry) ; L2 = 0,5 H ; L3 = 1,5 H ; Ln = 2 H.
Inductance totale : Lt = 0,5 + 0,5 + 1,5 + 2 = 4,5 H.
b) Données : L1 = 20 mH (millihenry ; 1 mH = 0,001 H) ; L2 = 5 mH.
Inductance totale : Lt = 20 + 5 = 25 mH.
c) Données : L1 = 300 µH (microhenry) ; L2 = 1 µH (0,000001 H) ; L3 = 50 µH ; L4 = 150 µH
Inductance totale : Lt = 300 + 1 + 50 + 150 = 501 µH.
![]() FORMULE 137 - Calcul de l'inductance équivalente
présentée par deux ou plusieurs bobines de valeur égale, reliées en parallèle et non couplées entre elles, connaissant leur
inductance.
FORMULE 137 - Calcul de l'inductance équivalente
présentée par deux ou plusieurs bobines de valeur égale, reliées en parallèle et non couplées entre elles, connaissant leur
inductance.
Énoncé : L'inductance présentée par deux ou plusieurs bobines égales reliées en parallèle, s'obtient en divisant leur inductance par le nombre de bobines.
Leq = L / n
Leq = inductance équivalente
L = inductance de chaque bobine
n = nombre de bobines reliées en parallèle
L'inductance équivalente sera exprimée dans la même unité de mesure que celle utilisée pour indiquer l'inductance des bobines.
-
Exemple :
a) Données : L = 2 H (henry) ; nombre (n) de bobine = 4
Inductance équivalente : Leq = 2 / 4 = 0,5 H.
b) Données : L = 50 mH (millihenry ; 1 mH = 0,001 H) ; n = 2
Inductance équivalente : Leq = 50 / 2 = 25 mH.
c) Données : L = 600 µH (microhenry ; 1 µH = 0,000001 H) ; n = 3
Inductance équivalente : Leq = 600 / 3 = 200 µH.
![]() FORMULE 138 - Calcul de l'inductance équivalente
de deux bobines de valeur différente, reliées en parallèle et non couplées entre elles, connaissant leur inductance.
FORMULE 138 - Calcul de l'inductance équivalente
de deux bobines de valeur différente, reliées en parallèle et non couplées entre elles, connaissant leur inductance.
Calcul de l'inductance équivalente de deux bobines de valeur différente
Énoncé : La somme des inductances présentées par deux bobines de différente inductance, reliées en parallèle, s'obtient en multipliant les deux valeurs et en divisant le produit obtenu par la somme de ces mêmes valeurs.
Leq = (L1 x L2) / (L1 + L2)
Leq = inductance équivalente
L1 = inductance d'une bobine
L2 = inductance de l'autre bobine.
Les valeurs d'inductance doivent toutes être exprimées dans la même unité de mesure.
-
Exemple :
Données : L1 = 12 mH (millihenry) ; L2 = 6 mH.
Inductance équivalente : Leq = (12 x 6) / (12 + 6) = 72 / 18 = 4 mH.
![]() FORMULE 139 - Calcul de l'inductance
d'une bobine à relier en parallèle à une autre bobine de valeur connue, pour
obtenir une inductance équivalente connue (les deux bobines ne doivent pas être
couplées entre elles).
FORMULE 139 - Calcul de l'inductance
d'une bobine à relier en parallèle à une autre bobine de valeur connue, pour
obtenir une inductance équivalente connue (les deux bobines ne doivent pas être
couplées entre elles).
Calcul de l'inductance d'une bobine à relier en parallèle à une autre bobine de valeur connue
Énoncé : L'inductance d'une bobine à relier en parallèle à une autre bobine, pour obtenir une inductance équivalente donnée, se calcule en multipliant la valeur de la bobine connue par l'inductance équivalente et en divisant le produit par la différence de ces valeurs.
Li = (L x Leq) / (L - Leq)
Li = inductance inconnue
L = valeur de la bobine disponible
Leq = inductance équivalente que l'on veut obtenir.
Les valeurs d'inductance doivent toutes être exprimées dans la même unité de mesure.
-
Exemple :
Données : L = 800 µH = 800 µH (microhenry) ; Leq = 600 µH
Inductance inconnue : Li = (800 x 600) / (800 - 600) = 480 000 / 200 = 2 400 µH
![]() FORMULE 140 - Calcul de l'inductance équivalente
de plusieurs bobines reliées en parallèle et non couplées entre elles, connaissant leur inductance.
FORMULE 140 - Calcul de l'inductance équivalente
de plusieurs bobines reliées en parallèle et non couplées entre elles, connaissant leur inductance.
Énoncé : L'inductance équivalente de plusieurs bobines reliées en parallèle, s'obtient en exécutant les calculs en trois temps : d'abord, on calcule l'inverse de l'inductance de chaque bobine, ce qui revient à diviser le nombre 1 par la valeur de la bobine ; ensuite, on additionne les valeurs des inverses ; enfin, on calcule l'inductance équivalente en divisant le nombre 1 par la somme des inverses.
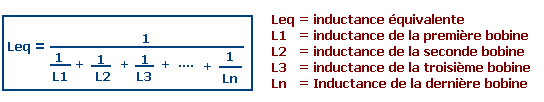
Les valeurs d'inductance doivent toutes être exprimées dans la même unité de mesure.
-
Exemple :
Données : L1 = 2 mH (millihenry) ; L2 = 4 mH ; L3 = 4 mH.
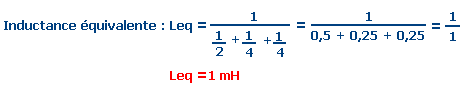
OBSERVATION :
Si l'on doit calculer l'inductance équivalente de deux bobines reliées en parallèle, on peut utiliser la formule 140, mais il est plus simple de recourir à la formule 138 ; en outre, dans le cas où les inductances des bobines reliées en parallèle sont égales entre elles, il convient de recourir à la formule 137.
![]() FORMULE 141 -
Calcul de l'énergie emmagasinée par une bobine, parcourue par un courant, connaissant l'inductance et l'intensité du courant.
FORMULE 141 -
Calcul de l'énergie emmagasinée par une bobine, parcourue par un courant, connaissant l'inductance et l'intensité du courant.
Calcul de l'énergie emmagasinée par une bobine
Énoncé : L'énergie emmagasinée par une bobine, exprimée en joules, s'obtient en multipliant l'inductance, exprimée en henrys par le carré de l'intensité du courant, exprimée en ampères et en divisant par 2 le produit obtenu.
W = (L x I2) / 2
W = énergie électrique en J (joule)
L = inductance en H (henry)
I = intensité du courant en A (ampère)
-
Exemple :
Données : L = 50 mH (millihenry) = 0,05 H ; I = 100 mA (milliampère) = 0,1 A
Énergie électrique emmagasinée :
W = (0,05 x 0,12) / 2 = 0,05 x 0,01 / 2 = 0,00025 J.
![]() FORMULE 142 - Calcul de la fréquence d'une
grandeur périodique (par exemple, d'un courant avec allure sinusoïdale),
connaissant la période, c'est-à-dire la durée de chaque cycle.
FORMULE 142 - Calcul de la fréquence d'une
grandeur périodique (par exemple, d'un courant avec allure sinusoïdale),
connaissant la période, c'est-à-dire la durée de chaque cycle.
Calcul de la fréquence d'une grandeur périodique par exemple, d'un courant avec allure sinusoïdale
Énoncé : La fréquence, exprimée en hertz, s'obtient en divisant le nombre 1 par la période exprimée en secondes.
f = 1 / T
f = fréquence en Hz (hertz)
T = période en s (seconde)
-
Exemple :
Donnée : T = 0,02 s.
Fréquence : f = 1 / 0,02 = 50 Hz.
OBSERVATION :
Si, dans la formule 142, la période est exprimée en millisecondes (ms ; 1 ms = 0,001 s), la fréquence sera exprimée en kilohertz, (kHz ; 1 kHz = 1 000 Hz) ; si au contraire, la période est exprimée en microsecondes (µs ; 1 µs = 0,000001 s), la fréquence sera exprimée en mégahertz (MHz ; 1 MHz = 1 000 000 Hz).
![]() FORMULE 143 - Calcul de la période d'une
grandeur périodique (par exemple, d'un courant alternatif avec allure sinusoïdale)
connaissant la fréquence, c'est-à-dire le nombre de cycles accomplis pendant
l'unité de temps.
FORMULE 143 - Calcul de la période d'une
grandeur périodique (par exemple, d'un courant alternatif avec allure sinusoïdale)
connaissant la fréquence, c'est-à-dire le nombre de cycles accomplis pendant
l'unité de temps.
Énoncé : La période, exprimée en secondes, s'obtient en divisant le nombre 1 par la fréquence, exprimée en hertz.
T = 1 / f
T = période en s (seconde)
f = fréquence en Hz (hertz)
-
Exemple :
Donnée : f = 1 000 Hz.
Période : T = 1 / 1 000 = 0,001 s
OBSERVATION :
Si, dans la formule 143, la fréquence est exprimée en kilohertz (kHz ; 1 kHz = 1 000 Hz), la période sera exprimée en millisecondes (ms ; 1 ms = 0,001 s) ; si, au contraire la fréquence est exprimée en mégahertz (MHz ; 1 MHz = 1 000 000 Hz), la période sera exprimée en microsecondes (µs ; 1 µs = 0,000001 s).
![]() FORMULE 144 -
Calcul de la valeur efficace d'un courant (ou tension) de type
alternatif et sinusoïdal, connaissant la valeur maximale.
FORMULE 144 -
Calcul de la valeur efficace d'un courant (ou tension) de type
alternatif et sinusoïdal, connaissant la valeur maximale.
Calcul de la valeur efficace d'un courant ou tension de type alternatif et sinusoïdal
Énoncé : La valeur efficace d'un courant (ou de tension) de type alternatif sinusoïdal s'obtient en divisant la valeur maximale par la racine carrée de 2.

REMARQUES :
En multipliant le numérateur et le dénominateur de cette formule par 1,41, on obtient également la formule simplifiée suivante :
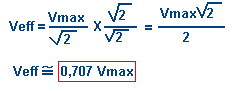
de même, on aura :
Ieff ![]() 0,707 x Imax
0,707 x Imax
Ieff = valeur efficace du courant en A (ampère)
Imax = valeur maximale du courant en A (ampère).
-
Exemple :
a) Donnée : valeur maximale du courant alternatif, Imax = 0,8 A (ampère).
Valeur efficace du courant alternatif : Ieff = 0,707 x 0,8 = 0,5656 A.
b) Donnée : valeur maximale de la tension alternative : Vmax = 311 V (volt).
Valeur
efficace de la tension alternative : Veff ![]() 0,707 x 311 = 220 V.
0,707 x 311 = 220 V.
OBSERVATION :
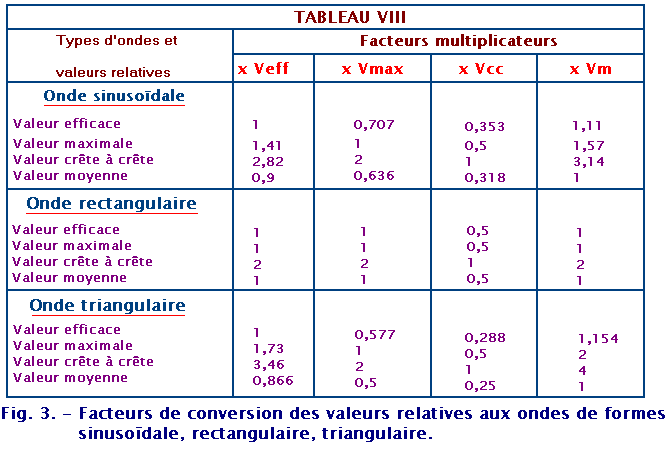
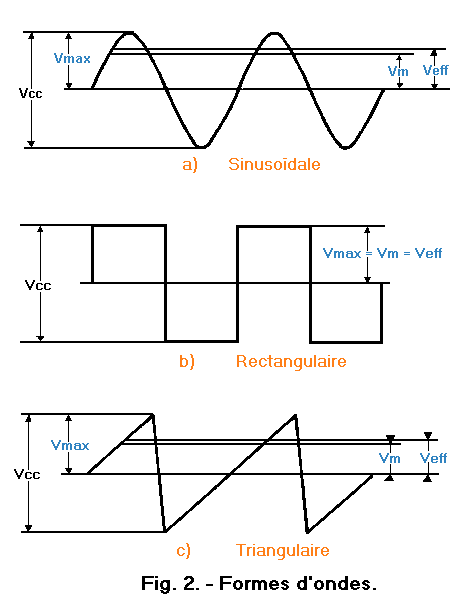
La valeur efficace d'un courant (ou tension) alternatif dépend aussi de la forme d'onde. En effet, si l'onde est sinusoïdale, (figure 2-a), la valeur efficace est égale au produit de la valeur maximale par le nombre 0,707 ; par contre, si l'onde est rectangulaire (figure 2-b) la valeur efficace est égale à la valeur maximale. Si l'onde est triangulaire (figure 2-c), la valeur efficace est égale au produit de la valeur maximale par le nombre 0,577 (tableau VIII, figure 3). En général, un nombre précis correspond à chaque forme d'onde, nombre compris entre zéro et 1, qui multiplié par la valeur maximale, permet d'obtenir la valeur efficace.
![]() FORMULE 145 - Calcul de la valeur maximale
d'un courant (ou tension) alternatif sinusoïdal, connaissant la valeur efficace.
FORMULE 145 - Calcul de la valeur maximale
d'un courant (ou tension) alternatif sinusoïdal, connaissant la valeur efficace.
Calcul de la valeur maximale d'un courant ou tension alternatif sinusoïdal
Vmax = Veff x 1,41
Vmax = valeur maximale de la tension en V (volt)
Veff = valeur efficace de la tension en V (volt)
Racine carrée de
2 ![]() 1,41
1,41
Imax = Ieff x 1,41
Imax = valeur maximale du courant en A (ampère)
Ieff = valeur efficace du courant en A (ampère)
(Les formules ci-dessus sont tirées des formules 144).
-
Exemple :
a) Donnée : valeur efficace du courant alternatif, Ieff = 2,5 A (ampère)
2,5 A. Valeur maximale du courant alternatif : Imax = 1,41 x 2,5 = 3,5
b) Données : valeur efficace de la tension alternative, Veff = 160 V.
Valeur maximale de la tension alternative, Vmax = 1,41 x 160 = 225,6 V.
OBSERVATION :
Le nombre qui multiplie la valeur efficace dépend de la forme d'onde. En effet, si l'onde est sinusoïdale (figure 2-a), on utilisera le facteur 1,414 ; mais si l'onde est rectangulaire (figure 2-b), on utilisera le facteur 1 et la valeur maximale sera donc égale à la valeur efficace ; en outre, si l'onde est triangulaire (figure 2-c), on utilisera le facteur 1,73 (tableau VIII, figure 3).
![]() FORMULE 146 -
Calcul de la valeur crête à crête d'une tension alternative sinusoïdale,
connaissant sa valeur efficace.
FORMULE 146 -
Calcul de la valeur crête à crête d'une tension alternative sinusoïdale,
connaissant sa valeur efficace.
Calcul de la valeur crête à crête d'une tension alternative sinusoïdale
Énoncé : La valeur crête à crête d'une tension alternative sinusoïdale, s'obtient en multipliant la valeur efficace par le nombre fixe 2,82.
Vcc = 2,82 x Veff
Vcc = valeur crête à crête de la tension
Veff = valeur efficace de la tension
Icc = 2,82 x Ieff
Icc = valeur crête à crête du courant
Ieff = valeur efficace du courant
-
Exemple :
Donnée : Valeur efficace de la tension alternative, Veff = 220 V (volt)
Valeur de crête à crête de la tension, Vcc = 220 x 2,82 = 620,4 V.
OBSERVATION :
Le nombre fixe qui multiplie la valeur efficace dépend de la forme d'onde. En effet, si l'onde est sinusoïdale (figure 2-a), on utilisera le facteur 2,82 ; mais si l'onde est rectangulaire (figure 2-b), on utilisera le facteur 2 (tableau VIII, figure 3) ; si au contraire, l'onde est triangulaire (figure 2-c), on utilisera le facteur 3,46 (tableau VIII, figure 3).
![]() FORMULE 147 - Calcul
de la valeur moyenne d'un courant (ou tension) alternatif sinusoïdal,
connaissant la valeur efficace.
FORMULE 147 - Calcul
de la valeur moyenne d'un courant (ou tension) alternatif sinusoïdal,
connaissant la valeur efficace.
Calcul de la valeur moyenne d'un courant ou tension alternatif sinusoïdal
Énoncé : La valeur moyenne d'un courant (ou tension) alternatif sinusoïdal s'obtient en multipliant la valeur efficace par le nombre fixe 0,9.
Vm = 0,9 x Veff
Vm = valeur moyenne de la tension en V (volt)
Veff = valeur efficace de la tension en V (volt)
Im = 0,9 x Ieff
Im = valeur moyenne du courant en A (ampère)
Ieff = valeur efficace du courant en A (ampère)
-
Exemple :
a) Donnée : Valeur efficace du courant alternatif, Ieff = 0,35 A (ampère)
Valeur moyenne du courant alternatif, Im = 0,9 x 0,35 = 0,315 A
b) Donnée : Valeur efficace de la tension alternative : Veff = 220 V.
Valeur moyenne de la tension alternative : Vm = 0,9 x 220 = 198 V.
OBSERVATION :
Le nombre fixe qui multiplie la valeur efficace dépend de la forme d'onde. En effet, si l'onde est sinusoïdale (figure 2-a), on utilisera le facteur 0,9 mais si l'onde est rectangulaire (figure 2-b), on utilisera le facteur 1 et de ce fait, la valeur moyenne sera égale à la valeur efficace ; enfin, si l'onde est triangulaire (figure 2-c), on utilisera le facteur 0,866 (tableau VIII, figure 3).
![]() FORMULE 148 - Calcul
de la pulsation d'une grandeur périodique, connaissant sa fréquence.
FORMULE 148 - Calcul
de la pulsation d'une grandeur périodique, connaissant sa fréquence.
Calcul de la pulsation d'une grandeur périodique
Énoncé : La pulsation, exprimée en radians par seconde, est donnée par deux fois le produit du nombre P par la fréquence, exprimée en hertz.
w
= 2 n f
![]() 6,28 f
6,28 f
w = pulsation en rd / s (radian par seconde)
P = symbole du nombre 3,14...
f = fréquence en Hz (hertz)
-
Exemple :
Donnée : f = 400 Hz
Pulsation : w
![]() 6,28 x 400
= 2 512 rd / s.
6,28 x 400
= 2 512 rd / s.
![]() FORMULE 149 - Calcul de la fréquence d'une
grandeur périodique, connaissant la pulsation.
FORMULE 149 - Calcul de la fréquence d'une
grandeur périodique, connaissant la pulsation.
Calcul de la fréquence d'une grandeur périodique
f = w
/ 2P
![]() 0,159 w
0,159 w
f = fréquence en Hz (hertz)
w = pulsation en rd / s (radian par seconde)
P = symbole de nombre fixe 3,14...
(Cette formule est tirée de la formule 148).
-
Exemple :
Donnée : w = 2 000 rd / s.
Fréquence : f ![]() 0,159 x 2 000 = 318 Hz.
0,159 x 2 000 = 318 Hz.
![]() FORMULE 150
-
Calcul de la pulsation d'une grandeur périodique, connaissant sa période.
FORMULE 150
-
Calcul de la pulsation d'une grandeur périodique, connaissant sa période.
Calcul de la pulsation d'une grandeur périodique
w = 2P /
T
![]() 6,28 / T
6,28 / T
w = pulsation en rd / s (radian par seconde)
P = symbole du nombre fixe 3,14...
T = période en s (seconde)
La présente formule s'obtient en remplaçant dans la formule 148, la fréquence f, par le second membre de la formule 142, soit : 1 / T.
-
Exemple :
Donnée : T = 0,02 s (période du courant alternatif à 50 Hz).
Pulsation : w = 6,28 / 0,02 = 314 rd / s
![]() FORMULE 151 - Calcul de la période d'une
grandeur périodique, connaissant sa pulsation.
FORMULE 151 - Calcul de la période d'une
grandeur périodique, connaissant sa pulsation.
Calcul de la période d'une grandeur périodique
T = 2P
/ w ![]() 6,28 / w
6,28 / w
T = période en s (seconde)
P = symbole du nombre fixe 3,14...
w = pulsation en rd / s (radian par seconde)
(Cette formule est tirée de la formule 150).
-
Exemple :
donnée : w = 628 rd / s (pulsation d'un courant alternatif à 100 Hz)
Période : T = 6,28 / 628 = 0,01 s.
![]() FORMULE 152 - Calcul
de la réactance capacitive d'un condensateur, connaissant la capacité du
condensateur et la fréquence du courant alternatif qui le traverse.
FORMULE 152 - Calcul
de la réactance capacitive d'un condensateur, connaissant la capacité du
condensateur et la fréquence du courant alternatif qui le traverse.
Calcul de la réactance capacitive d'un condensateur
Énoncé : La réactance capacitive, exprimée en ohms, s'obtient en divisant le nombre 1 par 6,28 (2P) par la fréquence, exprimée en hertz et par la capacité, exprimée en farads.
Xc = 1 / (2PfC)
![]() 1 / (6,28 fC)
1 / (6,28 fC)
Xc = réactance capacitive en W (ohm)
P = symbole du nombre fixe 3,14...
f = fréquence en Hz (hertz)
C = capacité en F (farad)
Cette formule s'écrit également :
Xc = 1 / Cw
puisque d'après la formule 148, w = 6,28 f.
-
Exemple :
Données : f = 3 000 Hz ; C = 500 nF (nanofarad) = 0,0000005 F.
Réactance capacitive : Xc ![]() 1 / (6,28 x 3 000 x 0,0000005) = 1 / 0,00942
1 / (6,28 x 3 000 x 0,0000005) = 1 / 0,00942 ![]() 106,15 W.
106,15 W.
OBSERVATION :
Dans les calculs, il est souvent plus commode de remplacer les unités de mesure de la fréquence et de la capacité par les multiples et sous-multiples correspondants ; en particulier, il arrive de trouver la fréquence exprimée en kilohertz (kHz) ou bien en mégahertz (MHz) et la capacité en nanofarads (nF), en picofarads (pF), ou bien en microfarads (µF). Dans tous ces cas, on peut utiliser la formule 152, en tenant compte de ce qui suit :
-
Si la fréquence est exprimée en hertz et la capacité en microfarads, la réactance sera exprimée en mégohms,
-
Si la fréquence est exprimée en kilohertz et la capacité en nanofarads, la réactance sera exprimée en mégohms,
-
Si la fréquence est exprimée en kilohertz et la capacité en microfarads, la réactance sera exprimée en kilo-ohms,
-
Si la fréquence est exprimée en mégahertz et la capacité en nanofarads, la réactance sera exprimée en kilo-ohms,
-
Enfin, si la fréquence est exprimée en mégahertz et la capacité en picofarads, la réactance sera exprimée en mégohms.
![]() FORMULE 153 - Calcul de la capacité d'un
condensateur, connaissant sa réactance capacitive pour une fréquence donnée.
FORMULE 153 - Calcul de la capacité d'un
condensateur, connaissant sa réactance capacitive pour une fréquence donnée.
Calcul de la capacité d'un condensateur
C = 1 / (2
P f Xc) ![]() 1 / (6,28 f Xc)
1 / (6,28 f Xc)
C = capacité en F (farad)
P = symbole du nombre fixe 3,14...
f = fréquence en Hz (hertz)
Xc = réactance capacitive en W (ohm)
(Cette formule est tirée de la formule 152).
-
Exemple :
Données : F = 5 000 Hz ; Xc = 400 W.
Capacité :
C ![]() 1 / (6,28 x 5 000 x 400) 1 / 12 560 000 = 0,000 000 079 617 F
1 / (6,28 x 5 000 x 400) 1 / 12 560 000 = 0,000 000 079 617 F
C ![]() 79,61 nF (nanofarad).
79,61 nF (nanofarad).
![]() FORMULE 154 - Calcul de la réactance
inductive d'une bobine, connaissant son inductance et la fréquence du courant alternatif qui la traverse.
FORMULE 154 - Calcul de la réactance
inductive d'une bobine, connaissant son inductance et la fréquence du courant alternatif qui la traverse.
Calcul de la réactance inductive d'une bobine
Énoncé : La réactance inductive, exprimée en ohms, s'obtient en multipliant le nombre fixe 6,28 (2P) par la fréquence, exprimée en hertz et par l'inductance, exprimée en henrys.
XL = 2
P
f L ![]() 6,28 f L
6,28 f L
XL = réactance inductive en W (ohm)
P = symbole du nombre fixe 3,14...
f = fréquence en Hz (hertz)
L = inductance en H (henry)
ou : XL = Lw Puisque w = 6,28 f (formule 148).
-
Exemple :
Données : f = 250 000 Hz ; L = 0,006 H.
Réactance inductive : XL = 6,28 x 250 000 x 0,006 = 9 420 W.
OBSERVATION :
La formule 154 peut aussi s'utiliser en exprimant la fréquence en kilohertz (kHz) et l'inductance en millihenrys (mH), ou bien la fréquence en mégahertz (MHz) et l'inductance en microhenrys (µH) ; dans l'un et l'autre cas, la réactance inductive sera exprimée en ohms.
![]() FORMULE 155
- Calcul de l'inductance d'une bobine, connaissant sa réactance inductive pour une fréquence
donnée.
FORMULE 155
- Calcul de l'inductance d'une bobine, connaissant sa réactance inductive pour une fréquence
donnée.
Calcul de l'inductance d'une bobine
L = XL / (2
P f) ![]() XL / 6,28 f
XL / 6,28 f
L = inductance en H (henry)
XL = réactance inductive en W (ohm)
P = symbole du nombre fixe 3,14...
f = fréquence en Hz (hertz)
(Cette formule est tirée de la formule 154).
-
Exemple :
Données : XL = 20 000 = 20 000 W ; f = 700 kHz (kilohertz) = 700 000 Hz.
Inductance
:
L = 20 000 / (6,28 x 700 000) = 20 000 / 4 396 000 ![]() 0,004 549 H
0,004 549 H
= 4,549 mH (millihenry).
(Nous terminons ainsi nos quatrièmes formulaires mathématiques et de rappels...).
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet.
|
|
 Page précédente Page précédente
|
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Calcul de la force magnétomotrice
Calcul de la force magnétomotrice