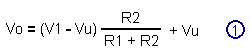 Réalisations pratiques des Triggers de Schmitt |
Trigger réalisé avec des portes NAND |
Applications des bascules de Schmitt
|
| Bas de page |
Les Bascules de Schmitt et leurs Applications :
2. - LES BASCULES DE SCHMITT
2. 1. - DÉFINITION ET FONCTION
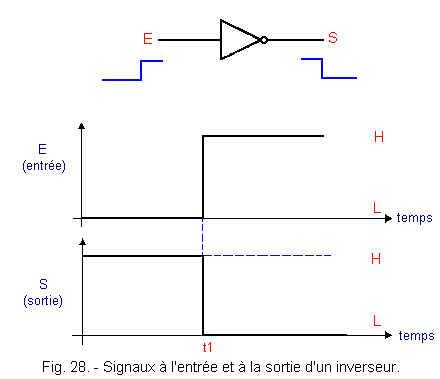
Une transition d'un niveau logique L à un niveau logique H, appliquée à l'entrée
d'un inverseur, peut être schématisée comme indiqué à la figure 28.
Schématisé ainsi, il apparaît que les signaux présents à
l'entrée et à la sortie de l'inverseur présentent des fronts bien droits,
c'est-à-dire que la tension varie instantanément d'un état logique à l'état logique complémentaire.
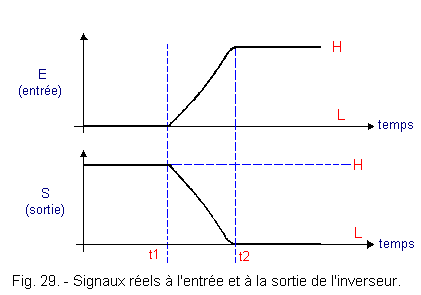
Or, ceci est une vision purement théorique. Les signaux réels
s'éloignent de cette représentation théorique et appliqués au même circuit
logique, auraient la forme représentée à la figure 29.
Il apparaît donc qu'un signal logique met un certain temps (ici
t2 - t1) pour passer d'un état logique à un autre.
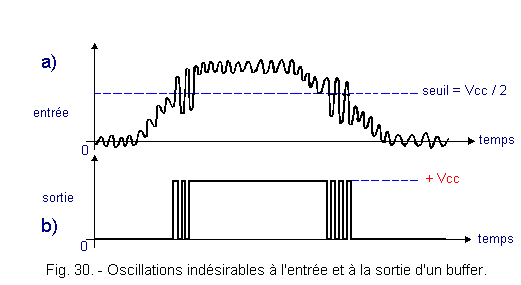
Une deuxième remarque s'impose. Si l'on se réfère à la
figure 30-a, il apparaît que la tension présente des variations dues aux parasites ou aux "bruits".
Ces derniers sont définis comme des perturbations ou des
variations de tension à petite échelle sur un signal électrique.
Un buffer peut être défini comme un amplificateur de courant,
c'est-à-dire un circuit conservant la forme du signal et augmentant la puissance disponible à sa sortie.
Ce buffer présente, par exemple, un seuil de basculement égal
à Vcc / 2, comme représenté à la figure 30-a. Or, le signal d'entrée possède des perturbations. En sortie, le signal
logique n'est donc pas stable mais présente des oscillations comme représenté à la figure 30-b.
En effet, les oscillations indésirables à l'entrée
franchissent à plusieurs reprises le seuil de basculement du buffer.
Il a donc été nécessaire de concevoir des circuits logiques
qui puissent palier ces deux types d'inconvénients.
Ce sont les bascules de Schmitt
ou encore triggers de Schmitt. L'idée
fondamentale est de créer deux seuils de basculement, l'un sur le front montant d'un signal, l'autre sur le front descendant de ce signal. Ceci est représenté
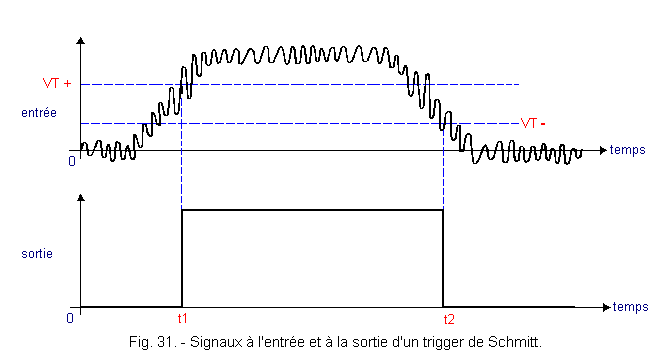
à la figure 31.
A l'instant t1, la tension présente à l'entrée atteint le seuil de basculement VT+,
la sortie passe très rapidement du niveau logique L au niveau logique H, bien que le seuil VT+
soit franchi plusieurs fois au cours des oscillations présentes à l'entrée du
trigger.
Au cours du front descendant, c'est à l'instant
t2 que le signal d'entrée franchit le seuil de basculement
VT-.
La sortie passe alors très rapidement du niveau logique
H au niveau logique
L.
Les deux instants de basculement sont les deux instants où le
signal franchit pour la première fois le seuil considéré. Il est évident que plus la différence (VT+) - (VT-) est
importante, plus ce circuit sera fiable et insensible aux fluctuations parasites superposées au signal originel. Cet écart de tension entre les deux seuils est
appelé hystérésis. C'est une caractéristique propre à un trigger de Schmitt. Le cycle d'hystérésis
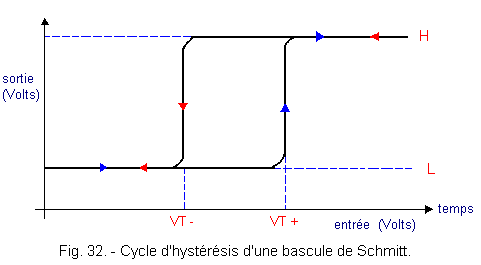
est représenté à la figure 32.
Les flèches sur ce schéma indiquent le sens de parcours des tensions à l'entrée et à la sortie du trigger.
Il apparaît clairement que la sortie passe du niveau
L au niveau H dès que le seuil VT+
est franchi à l'entrée de la bascule (flèche bleue). De même, il faut que la
tension d'entrée descende à VT- pour que
la sortie passe du niveau H au niveau L (flèche rouge).
La différence (VT+) - (VT-)
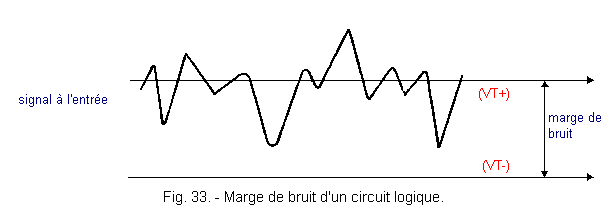
constitue également la "marge de bruit" qui est l'écart de tension qu'un
signal peut avoir sans entraîner d'incident particulier sur le fonctionnement d'un circuit. La figure 33 présente l'allure d'un signal présent à l'entrée
d'une bascule de Schmitt.
A un moment donné, l'entrée a franchi le seuil
VT+, la sortie est donc au niveau H.
On aperçoit les perturbations du signal d'entrée, mais ce
signal n'atteint jamais le seuil VT-, donc
l'entrée est considérée en permanence à l'état H.
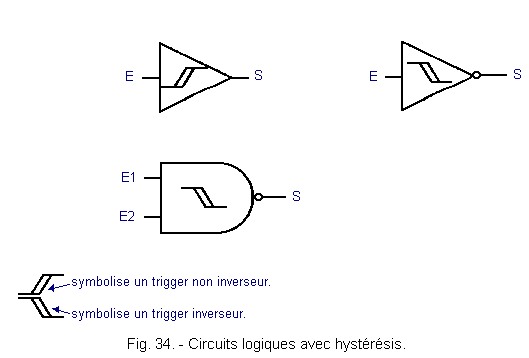
Le symbole suivant ( Des exemples sont donnés à la figure 34.
2. 2. 1. - TRIGGER DE BASE
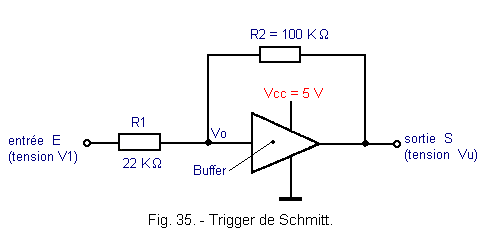
Dans le trigger de la figure 35, deux résistances R1 et R2 sont associées à un buffer.
Les deux résistances sont montées en pont diviseur de tension.
L'entrée du buffer a une résistance très élevée, de l'ordre de quelques dizaines de MW
(en technologie CMOS). L'effet de ce buffer sera donc négligé sur le pont diviseur de tension. Pour
cela, R1 et R2 auront des valeurs assez grandes. Par exemple, R1 = 22 k
et R2 = 100 kW.
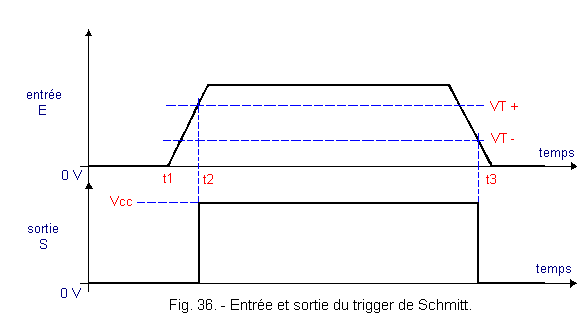
Dans ce cas, nous avons la relation Appliquons à l'entrée E le signal indiqué à la figure 36.
Au départ, V1 = Vu = 0 volt.
Au fur et à mesure que V1 augmente, la
tension d'entrée du buffer Vo augmente
aussi et Vu reste nulle. En effet, il faut
que Vo atteigne Vcc / 2 pour que la sortie S bascule
au niveau H.
La tension V1 nécessaire au
basculement du buffer est la tension de seuil supérieur
VT+.
A partir de la relation Juste avant le basculement, la tension Vo
est donc égale à Vcc / 2 et la tension de
sortie Vu est encore nulle. Remplaçons Vo
et Vu par leur valeur dans l'équation La tension V1
de basculement que l'on appelle VT+ est donc donnée par la
relation Si l'on remplace dans le cas présent R1 et R2 par leur valeur et sachant que la
tension d'alimentation est de 5 volts, on obtient une tension de basculement de :
Ceci est donc la valeur du seuil supérieur.
Tant que la tension V1 restera supérieure à la tension de seuil inférieur VT-,
la sortie S restera au niveau H (donc à la tension Vcc).
Quand la tension d'entrée V1 redescend, le buffer bascule au niveau L
pour Vo = Vcc / 2.
Calculons donc VT-
à l'aide de l'équation d'où : On obtient la relation Remplaçons R1, R2 et Vcc par leur valeur numérique :
Le seuil inférieur est donc de 1,95 volt.
L'hystérésis vaut (VT+) -
(VT-) = 3,05 - 1,95 = 1,1 volt.
Il serait par ailleurs possible d'augmenter la valeur de l'hystérésis
en prenant une valeur pour R1 supérieure à
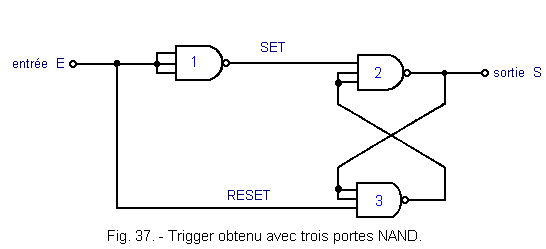
22 k Ici, nous n'utilisons pas de résistances. Ce trigger est représenté à la figure 37. Il comprend trois portes NAND
à trois entrées réalisées en technologie CMOS. Le fonctionnement de ce trigger utilise la propriété suivante : la
tension du seuil de basculement est fonction du nombre d'entrées reliées ensemble sur lesquelles est appliqué le signal de commande. Ce seuil sera
d'autant plus élevé qu'il y aura d'entrées reliées ensemble.
A l'état de repos, l'entrée E et la sortie S sont au niveau logique L.
Quand la tension à l'entrée augmente et atteint VT+, la porte 1 commute, l'entrée SET
passe au niveau L et la sortie S au niveau H.
Quand la tension à l'entrée E
redescend et franchi le seuil VT-, la porte
3 commute et sa sortie passe au niveau H. La sortie S commute également et repasse au
niveau L. Donc ce montage est bien un trigger possédant deux seuils de basculement VT+
et VT-. L'hystérésis
(VT+) - (VT-) vaut environ
1 / 3 de Vcc
soit 1,66 volt pour
Vcc = 5 volts.
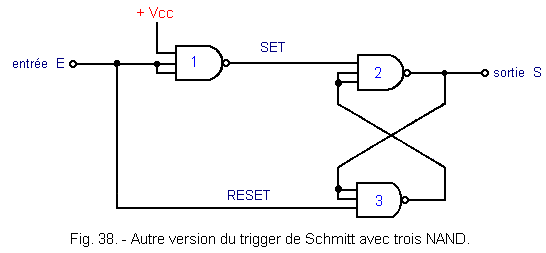
Si l'on veut réduire l'hystérésis à
1 / 6 de Vcc, il faut réunir
seulement deux entrées de la porte 1. Ceci est indiqué à la figure 38.
Ainsi, le seuil VT+ est
diminué.
Ce circuit particulier est souvent utilisé comme bascule de Schmitt disponible sous forme de circuit intégré de la famille CMOS.
Les applications des bascules de Schmitt sont nombreuses et quelques-unes ont déjà été traitées. C'est le cas lorsqu'il s'agit de débarrasser
certains signaux rectangulaires de parasites ou d'améliorer des fronts montants ou descendants qui varient trop lentement.
Dans le chapitre 3, le trigger sera présenté dans un montage astable.
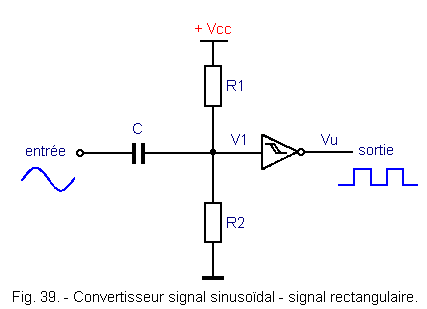
2. 3. 1. - TRANSFORMATION D'UNE SINUSOÏDE EN UN SIGNAL RECTANGULAIRE
Le montage est celui indiqué à la figure 39. A l'entrée est
appliqué un signal sinusoïdal de fréquence F.
A la sortie, on obtient un signal rectangulaire de fréquence identique F. Les deux résistances R1 et R2
constituent un pont diviseur de tension et C est un condensateur qui sert à découpler le signal d'entrée par rapport à
l'entrée du trigger de Schmitt.
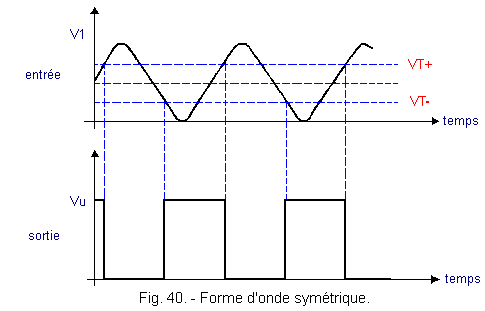
Si l'on veut obtenir un signal carré à la sortie, on choisira de fixer une tension V1 qui soit égale à
(VT+) - (VT-) /
2. Ceci apparaît clairement à la figure 40.
Ce montage peut servir à convertir une tension sinusoïdale
produite par une génératrice tachymétrique en un train d'ondes possédant une fréquence proportionnelle à la vitesse de rotation de la génératrice.
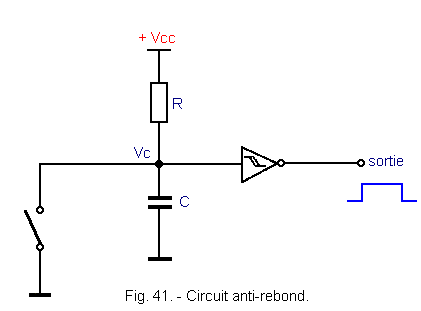
2. 3. 2. - CIRCUIT ANTI-REBOND
Dans le montage présenté à la figure 41, il s'agit de délivrer
une impulsion de tension sans que se manifeste un phénomène de rebond à la fermeture du contact.
A la fermeture de l'interrupteur, il y a rebondissement des contacts, mais le condensateur C limite les
variations de potentiel au point Vc et l'hystérésis du trigger permet de conserver le niveau logique H
en sortie.
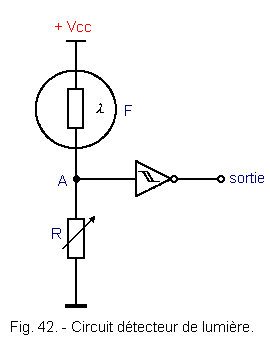
2. 3. 3. - DÉTECTEUR DE LUMIÈRE
Le montage de la figure 42 permet de détecter un certain seuil
de lumière pour commander, par exemple, l'extinction d'une lampe.
F est une résistance
photosensible dont la valeur diminue quand la lumière augmente.
Arrivé à un certain seuil d'éclairement, le point
A
dépasse le seuil VT+ du trigger de Schmitt
et la sortie bascule au niveau logique L.
Même si l'intensité lumineuse subit de légères fluctuations,
la sortie reste au niveau L.
Ce montage fonctionne également dans le sens
inverse. Quand l'intensité lumineuse diminue, le point
A franchit le potentiel VT-
et la
sortie repasse au niveau H.
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.
)
indique qu'un circuit logique possède un cycle d'hystérésis.
2. 2. - RÉALISATIONS PRATIQUES DES TRIGGERS DE SCHMITT
suivante :
précédente, exprimons cette tension V1 de
basculement.
.
.
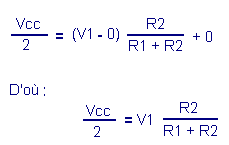
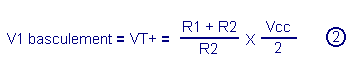
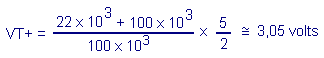
en remplaçant Vo par Vcc / 2 et Vu par Vcc.
:
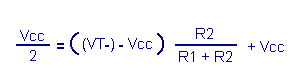
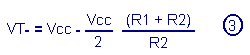
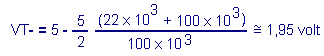
2. 2. 2. - TRIGGER RÉALISÉ AVEC DES PORTES
NAND
2. 3. - APPLICATIONS DES BASCULES DE SCHMITT
Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet.
Haut de page
Page précédente
Page suivante
Nombre de pages vues, à partir de cette date : le 15 JUILLET 2019
