 Bas de page |
Somme en Parallèle avec Retenue Série - Les Sommateurs :
1. 6. - SOMME EN PARALLÈLE AVEC RETENUE SÉRIE
La figure 13 représente un circuit de somme en parallèle de 8 bits avec retenue série.
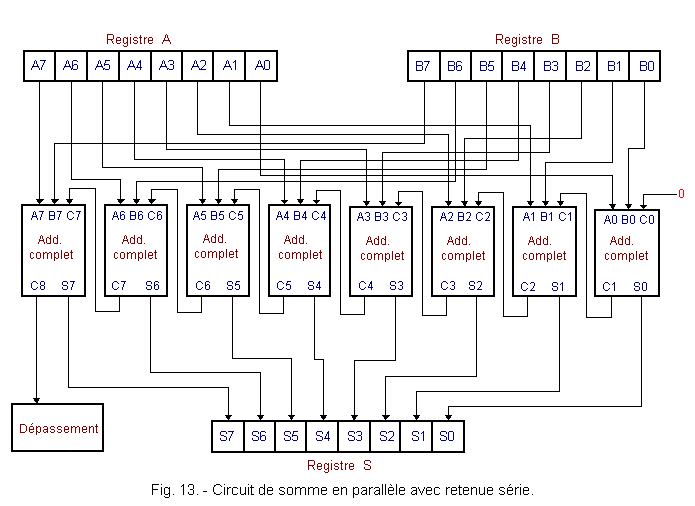
Nous constatons qu'un circuit de somme en parallèle nécessite autant d'additionneurs complets qu'il y a de chiffres à additionner.
D'autre part, puisque la sortie retenue d'un additionneur est reliée à l'entrée retenue du suivant, le circuit sommateur de la figure 13 est dit à retenue série. Il est à noter que l'entrée retenue C0 du premier additionneur doit être portée à l'état 0.
La méthode de la somme en parallèle est beaucoup plus rapide que celle de la somme en série et le temps total pour effectuer l'opération dépend essentiellement du temps requis pour la propagation de la retenue.
En effet, même si tous les chiffres sont additionnés simultanément, la retenue doit se propager du premier au dernier additionneur.
Ainsi, le résultat présenté sur les 8 sorties et sur la retenue C8 ne sera exact que lorsque cette propagation se sera effectuée.
Le mécanisme de l'addition est le suivant.
Le premier sommateur additionne les deux chiffres A0 et B0 et génère la somme S0 et la retenue C1.
Le deuxième sommateur additionne les chiffres A1 et B1 avec la retenue C1 produite par le premier sommateur. Il ne pourra additionner A1, B1 et C1 seulement lorsque la retenue C1 de la première somme aura été calculée par le premier sommateur.
Il faut donc attendre un certain temps que la retenue se soit propagée d'étage en étage pour que la somme S7 et la retenue C8 soient établis (les sommes S0 à S6 seront déjà établies). Avant ce temps, le résultat contenu dans S n'est pas forcément correct.
Ce mécanisme, semblable à celui rencontré dans les compteurs asynchrones, présente le même avantage (simplicité du circuit) et le même inconvénient (lenteur).
La méthode de somme en parallèle avec propagation de la retenue est cependant plus rapide que celle de la somme en série.
Le temps nécessaire pour qu'un additionneur complet calcule la retenue est très court, dans le cas des circuits C-MOS quelques dizaines de nanosecondes.
Toutefois, le temps total de l'addition est le produit de ce temps par le nombre de chiffres à additionner.
Il ne peut plus alors être négligé surtout dans les ordinateurs qui doivent pouvoir effectuer des millions d'addition par seconde. On a recours à la méthode de somme en parallèle à retenue anticipée.
1. 7. - SOMME EN PARALLÈLE À RETENUE ANTICIPÉE
Pour effectuer la somme plus rapidement, il faut compliquer le circuit précédent.
On se base sur le fait que les termes de la somme sont connus et disponibles avant même que commence l'opération d'addition. On peut alors calculer, en anticipant, la retenue pour chaque étage indépendamment des étages précédents. Il s'agit de pouvoir disposer de toutes les retenues simultanément et dans un temps le plus court possible.
Autrement dit, il faut calculer la retenue C1 à partir des bits A0, B0 et C0, la retenue C2 à partir des bits A0, B0, C0, A1 et B1 et ainsi de suite.
La figure 14 montre le synoptique d'un additionneur 4 bits à retenue anticipée.
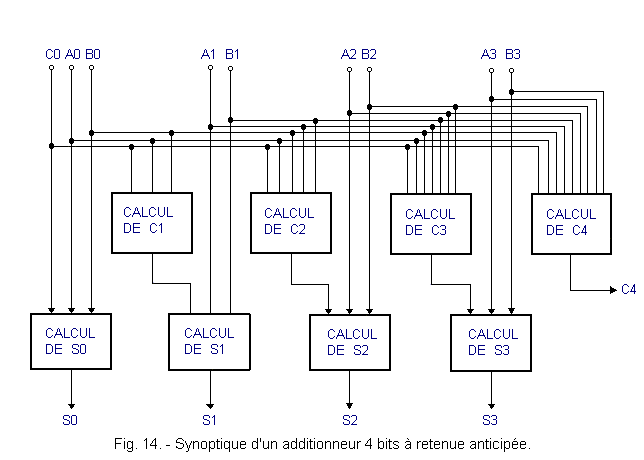
Pour effectuer le calcul des retenues de façon anticipée, il faut transformer l'équation de la retenue Ci + 1 vu précédemment.
Ci + 1 = Ai
iCi
+ AiBi + 
iBiCi
Puisque Ci + 1 vaut 1 lorsque Ai = Bi = Ci = 1, on peut ajouter les termes AiBiCi à l'expression de Ci + 1 autant de fois que l'on veut (ici 2 fois).
-
D'où Ci + 1 = Ai
iCi
+ AiBiCi + AiBi + 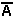iBiCi
+ AiBiCi -
= AiCi (
i
+ Bi) + AiBi + BiC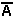i (i
+ Ai) -
Soit Ci + 1 = AiCi + AiBi + BiCi
-
= AiBi + Ci (Ai + Bi)
Posons : produit AiBi = pi et somme Ai + Bi = Si
D'où Ci + 1 = pi + CiSi
L'expression de la retenue du premier étage devient :
C1 = p0 + C0S0
et celle du deuxième étage :
C2 = p1 + C1S1
Remplaçons C1
par sa valeur calculée en
dans cette expression de C2
:
-
C2 = p1 + (po + C0S0) S1
-
C2 = p1 + poS1 + C0S0S1
De même :
-
C3 = p2 + C2S2
-
= p2 + (p1 + p0S1 + C0S0S1) S2
-
C3 = p2 + p1S2 + p0S1S2 + C0S0S1S2
-
C4 = p3 + C3S3
-
= p3 + (p2 + p1S2 + p0S1S2 + C0S0S1S2) S3
-
C4 = p3 + p2S3 + p1S2S3 + p0S1S2S3 + C0S0S1S2S3
Les expressions ,
,
,
et
des retenues C1, C2, C3 et
C4
sont remarquables par le fait qu'elles réclament le même temps de calcul et
qu'elles ne tiennent pas compte de la retenue de l'étage précédent (donc pas
de retard dû à la propagation de la retenue.
Pour expliquer cela, nous allons parler de «couche logique».
Une couche logique correspond au temps de propagation d'une porte élémentaire type ET ou OU.
Par exemple, le calcul de C1 = p0 + C0S0 nécessite 3 couches logiques comme le montre la figure 15.
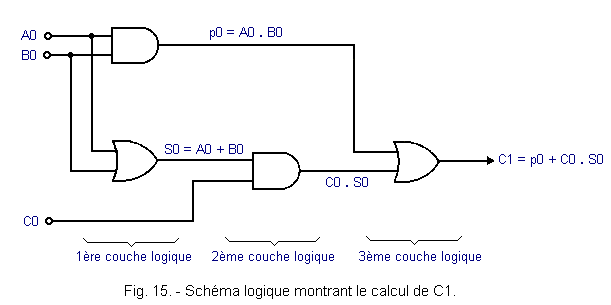
Bien que les expressions
,
et
des retenues C2, C3
et C4 soient plus complexes, celles-ci ne nécessitent
pour leur calcul que 3 couches logiques
comme C1.
Nous allons voir maintenant un exemple d'additionneur intégré 4 bits à retenue anticipée : le 7483.
La figure 16 présente le brochage et le schéma logique du circuit intégré 7483.
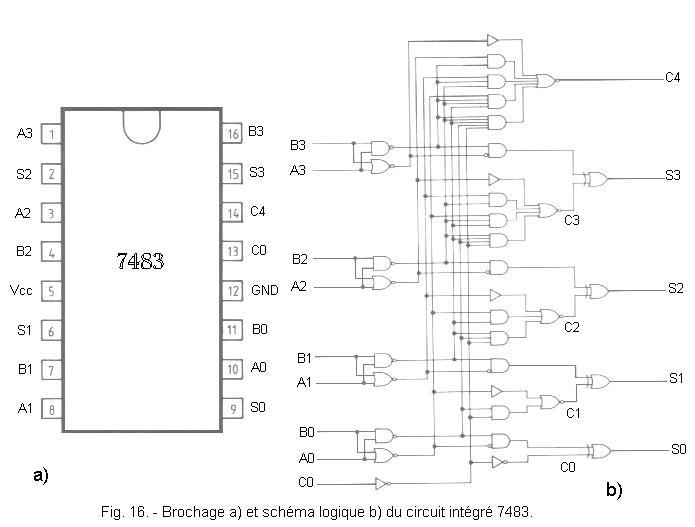
Les temps de propagation des différentes entrées vers les différentes sorties du circuit sont rassemblés dans le tableau de la figure 17.
| Entrées | Sorties | Temps maximal de propagation (en ns) |
| C0 | Si | 21 |
| Ai ou Bi | Si | 24 |
| C0 | C4 | 16 |
| Ai ou Bi | C4 | 16 |
Avec ce circuit intégré, on additionne 2 nombres de 4 bits en 24 ns maximum.
Il est à noter que le circuit intégré 74LS83 qui est un additionneur de 4 bits à retenue série effectue la même opération en 72 ns maximum, soit 3 fois plus.
Si l'on veut additionner 2 nombres de plus de 4 bits, il faut utiliser plusieurs additionneurs intégrés et les relier en cascade.
Pour exemple, la figure 18 montre la mise en cascade de 2 additionneurs 4 bits type 7483 pour obtenir un additionneur 8 bits. Il suffit de relier la sortie C4 du premier additionneur à l'entrée C0 du second.
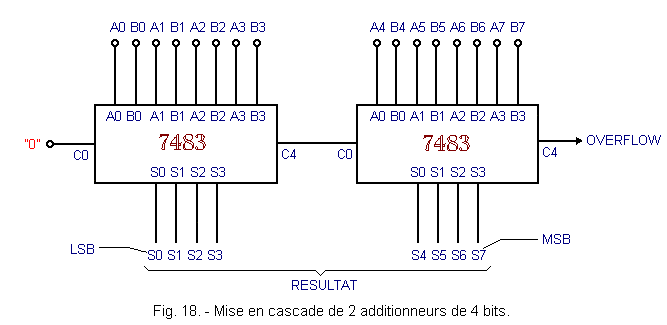
L'additionneur obtenu n'est que partiellement à retenue anticipée.
En effet, on retrouve le mécanisme de la retenue à propagation série dû à la sortie C4 reliée à l'entrée C0.
D'après le tableau de la figure 17, la sortie C4 du premier 7483 est disponible au bout de 16 ns. D'autre part, comme les sorties S4 à S7 sont disponibles 21 ns après l'apparition de la retenue en C0 du deuxième 7483, nous en déduisons que le résultat de la somme des 2 nombres de 8 bits est disponible après 16 + 21 = 37 ns maximum.
Chaque nouvel additionneur 7483 mis en cascade apporte un retard supplémentaire de 21 ns. Ainsi avec 3 circuits 7483, l'addition de 2 nombres de 12 bits nécessitera 37 + 21 = 58 ns maximum.
Après les additionneurs, examinons à présent les circuits comparateurs.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
 Haut de page |
|
Page précédente |
 Page suivante |
Nombre de pages vues, à partir de cette date : le 15 JUILLET 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.