LES CODES ET LES DÉCODEURS - LES CODES DE NUMÉRATION

**Signets :**
Les codes de numération	Nombre Binaire à la valeur Décimale correspondante	Les bits
	Bas de page

Les Codes et les Décodeurs - Codes de Numération - Bits :

Dans cette théorie, vous allez revoir des notions, déjà abordées en théorie 7, mais sous une forme plus simple. Ces notions concernent les codes et les systèmes de numération.

Vous verrez ensuite la manière de passer d'un code à l'autre et d'afficher les informations.

1. - LES CODES ET LES DÉCODEURS

1. 1. - L'INFORMATION ET LES CODES

Les feux tricolores (figure 1) permettent de diriger le trafic à l'intérieur des villes.

En effet, chaque usager de la route reçoit des informations codées sur la conduite qu'il doit adopter.

Orange : ralentissez

Rouge : arrêtez-vous

Vert : passez.

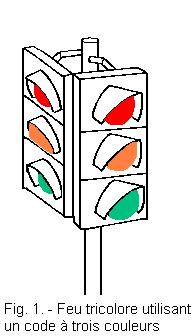
Dans la vie quotidienne, la communication implique un langage codé.

Le numéro national de la Sécurité Sociale est, par exemple, un code qui permet de reconnaître les individus afin par la suite de pouvoir faire réaliser par un ordinateur toutes les opérations relatives à leurs remboursements médicaux au titre de l'assurance sociale. Un exemple est donné figure 2.

Le langage et l'écriture sont aussi des moyens de communication en code. Ceci suppose qu'il y ait une règle liant celui qui écrit et celui qui lit le message.

Les insectes communiquent entre eux de différentes manières, c'est-à-dire avec différents codes :

Les abeilles possèdent différentes façons de voler pour conduire les autres abeilles en un lieu précis ou les avertir du danger, c'est ce que l'on appelle la danse des abeilles.

Certains animaux émettent des substances chimiques appelées «phéromones» qui permettent par exemple de marquer leur territoire, ou d'attirer leur partenaire ; d'autres comme les lucioles envoient des messages lumineux.

Tous ces exemples pourraient se multiplier à l'infini.

Les ordinateurs ou les circuits numériques ne peuvent eux aussi se passer de codes pour communiquer entre eux.

Puisque, comme nous l'avons vu, les circuits numériques fonctionnent avec deux niveaux : haut (H) et bas (L) ; tous les codes ne pourront utiliser que deux informations élémentaires liées à ces deux niveaux 1 et 0 (figure 3).

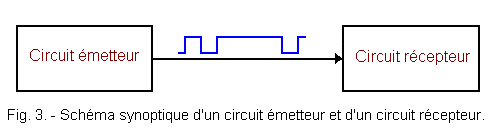
Toutefois, les possibilités offertes par des combinaisons de 1 et de 0 sont très nombreuses. Leur choix dépendra des applications souhaitées.

De la même façon, les lettres de l'alphabet ne sont pas nombreuses mais elles permettent pourtant de composer une infinité de mots et ce dans de nombreuses langues.

Malheureusement, il est impossible de connaître toutes les langues du monde, c'est pourquoi il est nécessaire de disposer d'interprètes.

Dans les circuits numériques, le problème est identique. Pour qu'un circuit utilisant un code x puisse converser avec un circuit utilisant un code y, il faudra un interprète que nous appellerons décodeur x / y (figure 4) ou décodeur y / x suivant le sens dans lequel la conversion de code s'effectuera (d'où les termes «x vers y» ou «y vers x» que vous rencontrerez plus loin).

Le décodeur traduit l'information d'un code dans un autre d'où également le terme transcodeur.

Nous examinerons les principaux codes numériques et les décodeurs correspondants.

1. 2. - LES CODES DE NUMÉRATION

Les informations traitées dans les circuits numériques sont matérialisées par des niveaux H et L représentatifs de valeurs logiques 1 et 0.

Nous avons vu que ces deux signes sont suffisants pour exprimer une information en code binaire.

Nous savons par ailleurs que le système de numération que nous utilisons chaque jour est différent. C'est le système décimal qui utilise 10 signes de 0 à 9.

1. 2. 1. - ORIGINE DE LA NUMÉRATION DÉCIMALE

Lorsque les anciens ont voulu compter des objets (ici des épis de blé), ils ont dû imaginer des nombres et les signes correspondants.

Un exemple est donné à la figure 5.

A chaque quantité d'objets correspond un nombre symbolisé par un signe graphique. Mais très rapidement, le problème devint impossible car à chaque fois que l'on ajoutait un objet, il fallait inventer un nouveau symbole.

Les signes de 0 à 9 nous sont familiers, mais ils pourraient être différents, ainsi les Romains utilisaient le signe V pour 5 et pour 10 le signe X que nous avons repris ici.

Les signes Ñ et inventés pour les besoins du cours signifient pour Ñ, 11 et pour , 12.

Pour compter jusqu'à 10 000, il faudrait 10 000 signes et pour compter jusqu'à l'infini une infinité de signes.

Les chaldéens trouvèrent la solution.

L'idée fut de se limiter à dix signes de 0 à 9, c'est-à-dire autant que les doigts des mains et d'exprimer chaque nombre aussi grand fut-il par une combinaison de ces dix signes.

Ainsi ne disposant que de 10 signes, arrivé à 9 a-t-on décidé de recommencer à 0 et d'indiquer 1 pour la première dizaine.

Ainsi pour X, on peut écrire 10 = 1 dizaine + 0 unité ;

pour Ñ, on peut écrire 11 = 1 dizaine + 1 unité ;

pour , on peut écrire 12 = 1 dizaine + 2 unités.

Ainsi, les signes 20 signifient : 2 dizaines + 0 unité.

Nous voyons que ce système permet d'écrire des nombres dont la structure est telle que pour 3 472₁₀ par exemple, ce nombre signifie :

3 (10³) + 4 (10²) + 7 (10¹) + 2 (10⁰)

Le premier chiffre à droite est celui des unités de poids 10⁰ = 1, le second en partant de la droite a un poids de 10¹ = 10, c'est le chiffre des dizaines, le troisième en partant de la droite a un poids de 10² = 100, c'est le chiffre des centaines et ainsi de suite.

Nous voyons que le poids des chiffres est multiplié par 10 à chaque fois que le chiffre se décale d'un rang vers la gauche. Nous appellerons 10, base du système.

Ainsi, dans 1 000 = 10 x 10 x 10 = 10³, 10 est la base et 3 l'exposant qui indique combien de fois la base doit être multipliée par elle-même.

1. 2. 2. - NUMÉRATION BINAIRE

Dans la numération binaire comme nous ne disposons que de deux chiffres, la base sera 2 et nous pourrons reprendre le problème des épis de blé comme représenté à la figure 6.

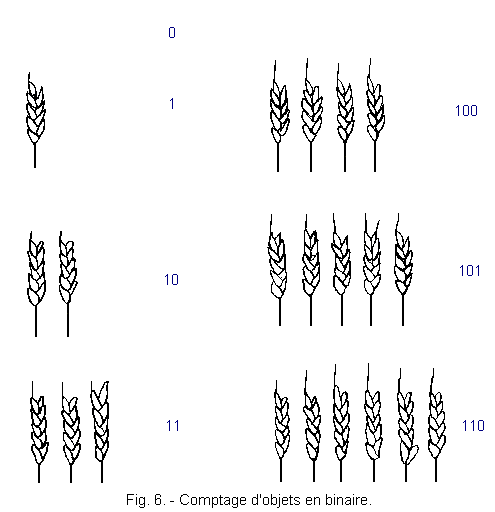
Ainsi pour aucun épis de blé, nous avons : 0 x 2⁰ = 0
pour un épi de blé 1 x 2⁰ = 1
pour deux épis de blé 1 (2¹) + 0 (2⁰) = 10
pour trois épis de blé 1 (2¹) + 1 (2⁰) = 11
pour quatre épis de blé 1 (2²) + 0 (2¹) + 0 (2⁰) = 100
pour cinq épis de blé 1 (2²) + 0 (2¹) + 0 (2¹) = 101
pour six épis de blé 1 (2²) + 1 (2¹) + 0 (2¹) = 110

Ces deux types de numération, binaire et décimale, constituent un type de code appelé code pondéré.

Dans le tableau de la figure 7, on trouve les vingt premiers nombres exprimés en code décimal pondéré et en code binaire pondéré.

Pour exprimer des nombres de plus en plus grand, il est nécessaire d'avoir de plus en plus de chiffres.

**Fig. 7. - Nombres de 0 à 20 représentés dans les deux codes pondérés décimal et binaire**.
Nombre	Code décimal pondéré	Code binaire pondéré
0	00	00000
1	01	00001
2	02	00010
3	03	00011
4	04	00100
5	05	00101
6	06	00110
7	07	00111
8	08	01000
9	09	01001
10	10	01010
11	11	01011
12	12	01100
13	13	01101
14	14	01110
15	15	01111
16	16	10000
17	17	10001
18	18	10010
19	19	10011
20	20	10100

Une combinaison de 4 chiffres binaires peut représenter l'un des 16 nombres compris entre 0 et 15.

Nota :

Chaque nombre binaire est représenté dans cette figure par un code de cinq chiffres constitué en ajoutant à gauche les 0 significatifs nécessaires.

Il est utile de savoir quel est le nombre maximum que l'on peut représenter avec un nombre déterminé de chiffres binaires. On peut le déterminer en lisant la valeur numérique maximale lorsque chaque chiffre est à 1 comme indiqué à la figure 8. Celle-ci donne l'exemple d'un nombre de 4 chiffres binaires.

Le nombre maximum que l'on peut représenter avec n chiffres binaires est : 2ⁿ- 1.

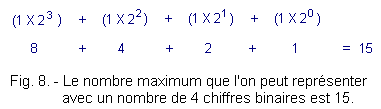
1. 3. - PASSAGE D'UN NOMBRE BINAIRE A LA VALEUR DÉCIMALE CORRESPONDANTE

Il suffit de donner à chaque chiffre binaire son poids et ensuite additionner les poids des différents chiffres.

Si nous prenons par exemple le nombre 10112 :

10112 = 1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰

= 1 x 8 + 0 x 4 + 1 x 2 + 1 x 1 = 8 + 0 + 2 + 1 d'où 10112 = 1110

Pour faire l'opération inverse, c'est-à-dire pour passer d'un nombre décimal au nombre binaire correspondant, on peut diviser de manière répétitive ce nombre par deux.

Les restes de chaque division constituerons les chiffres du nombre binaire en les lisant à partir du dernier. Rappelez-vous que le reste est 0 lorsque le dividende est pair et 1 lorsqu'il est impair.

Pour le nombre 277, on obtient par exemple :

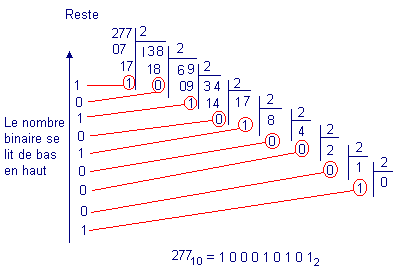
Donc à 27710 correspond le nombre binaire 1000101012. En effet, si l'on décompose le nombre selon le code binaire, on obtient :

1000101012 = (1 x 2⁸) + (0 x 2⁷) + (0 x 2⁶) + (0 x 2⁵) + (1 x 2⁴) + (0 x 2³) + (1 x 2²) + (0 x 2¹) + (1 x 2⁰)

= (1 x 256) + (0 x 128) + (0 x 64) + (0 x 32) + (1 x 16) + (0 x 8) + (1 x 4) + (0 x 2) + (1 x 1)

= 256 + 16 + 4 + 1 = 277

A tous les nombres binaires écrits avec les chiffres 0 et 1 correspondent autant de nombres décimaux écrits avec des chiffres décimaux.

Par exemple, le nombre binaire 1112 dont la valeur est égale à sept (710) pourrait aussi bien représenter le nombre décimal 11110 dont la valeur est égale à 111.

Afin d'éviter les confusions de ce genre, on écrit l'indice 2 pour les nombres binaires et l'indice 10 pour les nombres décimaux.

En procédant ainsi, on aura :

11110 si le nombre est décimal et vaut 111 ;
1112 si le nombre est binaire et vaut 710.

1. 4. - LES BITS

Les nombres binaires sont formés des chiffres 0 et 1. Ces chiffres binaires sont appelés «binary digit», en abrégé «bit».

Par la suite, le terme bit a pris en sens plus large que celui de chiffre binaire. Il indique plus généralement l'unité d'information qui peut être mémorisée dans une bascule.

N'importe quelle information de quelque type qu'elle soit peut être exprimée pour une succession appropriée de bits. Ainsi peut-on numériser la parole (téléphone numérique), l'écriture (traitement de texte), la musique (disque numérique), le calcul mathématique ou financier (calculateurs, ordinateurs et facturières).

Dans les ordinateurs, chaque information est décomposée en une succession de bits. Aucun ordinateur ne peut traiter plus d'un bit à la fois.

En compensation, par son extraordinaire rapidité, il est en mesure d'effectuer des opérations logiques ou arithmétiques de façon tellement rapide qu'il accomplit des tâches incroyablement complexes en un temps extrêmement bref.

En règle générale, on utilise assez souvent le mot bit pour indiquer le nombre d'étages, d'un compteur par exemple. On parle communément de compteurs ou registres à décalages à 4 bits, 8 bits, 12 bits ce qui signifie qu'il y a 4, 8, 12 bascules.

Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet.	Haut de page
Page précédente	Page suivante

Nombre de pages vues, à partir de cette date : le 15 JUILLET 2019

Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.

Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.

Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.