Notion de Fonction - 2ème Partie :
NOTION DE FONCTION "2ème PARTIE"
5. - FONCTION y = ax + b
5. 1. - ÉTUDE CONCRÈTE
Supposons qu'un cycliste se repose à un moment donné de sa randonnée en un point P situé à 20 km d'une ville 0. Il reprend sa route en s'éloignant de cette ville 0 à la vitesse de 15 km / h.
a) A quelle distance de la ville 0 se trouvera-t-il au bout de 1 heure ? 2 heures ? 3 heures ? etc...
b) Quel est le graphique pouvant représenter la distance parcourue en fonction du temps ?
Solution :
a) Nous savons que la distance parcourue par une personne ou un objet qui se déplace, on dit un "mobile", est fonction de la vitesse de ce mobile et de son temps de déplacement.
![]() La distance parcourue par le cycliste en une heure est 15 x 1 = 15 km. Il se retrouve donc éloigné
de la ville 0 de 15 + 20 = 35 km (point P1 figure 7).
La distance parcourue par le cycliste en une heure est 15 x 1 = 15 km. Il se retrouve donc éloigné
de la ville 0 de 15 + 20 = 35 km (point P1 figure 7).
![]() En deux heures, il parcourt : 15 x 2 = 30 km. Il se retrouve alors 30 + 20 =
50 km de 0 (point P2).
En deux heures, il parcourt : 15 x 2 = 30 km. Il se retrouve alors 30 + 20 =
50 km de 0 (point P2).
Généralisons : en x heures, le cycliste parcourt 15 . x km. Il se retrouve alors à 15 x + 20 km de 0.
Désignons par y la distance cycliste - ville 0. La relation qui relie cette distance (y) au temps de parcours (x) peut donc s'écrire :
y = 15x + 20
Si l'on remplace les nombres 15 et 20 par les lettres a et b, appelées paramètre, c'est-à-dire des lettres représentant des nombres quelconques mais connus, la relation devient :
y = ax + b
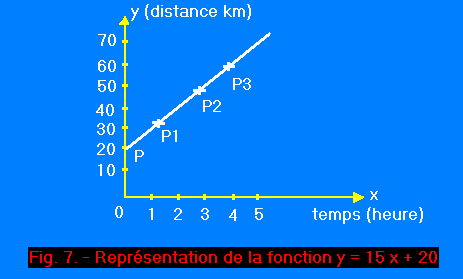
b) Représentons graphiquement la fonction y = 15 x + 20. Prenons en échelle 1 cm = 10 km et 1 cm = 1 heure.
Déterminons les points P1, P2, P3, etc... ayant pour coordonnées respectives les valeurs correspondantes de x et de y (figure 7).
|
Point P x = 0 |
y = (15 X 0) + 20 = 20 |
|
Point P1 x = 1 |
y = (15 X 1) + 20 = 35 |
|
Point P2 x = 2 |
y = (15 X 2) + 20 = 50 |
|
Point P3 x = 3 |
y = (15 X 3) + 20 = 65 etc.... |
En joignant les points les uns aux autres, on constate qu'ils sont alignés et qu'en conséquence la courbe représentative de la fonction y = 15x + 20 est une droite.
5. 2. - REPRÉSENTATION DE LA FONCTION y = ax + b
En généralisant ce qui vient d'être dit, on peut écrire :
La courbe représentative de la fonction y = ax + b est une droite parallèle à la droite y = ax et coupant l'axe des ordonnées au point d'ordonnée b.
Remarques et définitions :
![]() Le nombre b est appelé l'ordonnée à l'origine (valeur de y
pour x = 0),
Le nombre b est appelé l'ordonnée à l'origine (valeur de y
pour x = 0),
![]() La droite y = ax + b étant parallèle à la droite y = ax a
la même pente ; le paramètre "a" est donc la pente (ou coefficient angulaire) de la droite y
= ax + b.
La droite y = ax + b étant parallèle à la droite y = ax a
la même pente ; le paramètre "a" est donc la pente (ou coefficient angulaire) de la droite y
= ax + b.
![]() Si "a" est positif, la fonction y = ax est croissante.
Les deux droites étant parallèles, la fonction y = ax + b est également croissante.
Si "a" est positif, la fonction y = ax est croissante.
Les deux droites étant parallèles, la fonction y = ax + b est également croissante.
![]() Le paramètre "b" peut être positif ou négatif. S'il est nul, l'équation se réduit à y
= ax.
Le paramètre "b" peut être positif ou négatif. S'il est nul, l'équation se réduit à y
= ax.
![]() Pour la même raison, si "a" est négatif, la fonction y = ax et par conséquent
la fonction y = ax + b sont décroissantes.
Pour la même raison, si "a" est négatif, la fonction y = ax et par conséquent
la fonction y = ax + b sont décroissantes.
En résumé, dans la fonction y = ax + b :
-
a est la pente ;
-
b est l'ordonnée à l'origine, positive ou négative ;
-
si a > 0 la fonction est croissante ;
-
si a < 0 la fonction est décroissante.
5. 3. - TRACÉ PRATIQUE DE LA DROITE y = ax + b
Pour construire la droite y = ax + b, il suffit, bien entendu, de déterminer deux de ses points et de les joindre. En général, on détermine les points qui résultent de l'intersection de cette droite avec les axes de coordonnées :
on fait x = 0 et on calcule y ;
puis y = 0 et on calcule x.
Premier exemple : Soit la fonction y = - 2x + 4
![]() Prenons comme échelle :
Prenons comme échelle :
-
pour l'axe des abscisses 2 cm = une unité
-
pour l'axe des ordonnées 1 cm = une unité
![]() Traçons les deux axes (figure 8)
Traçons les deux axes (figure 8)
![]() Posons x = 0 ;
la relation y = - 2x + 4 devient :
Posons x = 0 ;
la relation y = - 2x + 4 devient :
y = 0 + 4 = 4 (points P1)
![]() Posons y = 0 ;
la relation y = - 2x + 4 devient :
Posons y = 0 ;
la relation y = - 2x + 4 devient :
|
0 = - 2x + 4 |
d'où |
2 x = 4 |
soit |
x = 2 (point P2) |
Prix à payer = nombre de kWh consommés x prix du kWh
Ce qui est de la forme : y = ax en attribuant "y" au prix à payer, "x" au nombre de kWh consommés et "a", paramètre connu, au prix du kWh c'est-à-dire 48 centimes.
Il reste à tenir compte de la location du compteur qui est fixe et indépendante de la consommation. Nous avons là, le facteur b et nous pouvons écrire : y = ax + b.
Avec y = montant de la redevance
a = prix du kWh (0,48 F)
x = nombre de kWh consommés
b = location du compteur (250 francs)
et, numériquement : y = 0,48x + 250
La relation étant établie, il nous faut transposer graphiquement.
Pour tracer et graduer les axes de coordonnées, choisissons les échelles :
- Axe des abscisses. Nous avons une consommation maximale de 1200 kWh. En prenant un axe de 10 cm, nous obtenons 1200 / 10 = 120 kWh par centimètre.
- Axe des ordonnées. Au maximum, la redevance sera de :
(0,48 X 1 200) + 250 = 576 + 250 = 826 francs.
Avec un axe de 10 cm, nous obtenons 826 / 10 = 82,6 F par centimètre. Pour plus de commodité, nous prendrons 100 F par centimètre.
![]() Traçons et graduons les deux axes (figure 9).
Traçons et graduons les deux axes (figure 9).
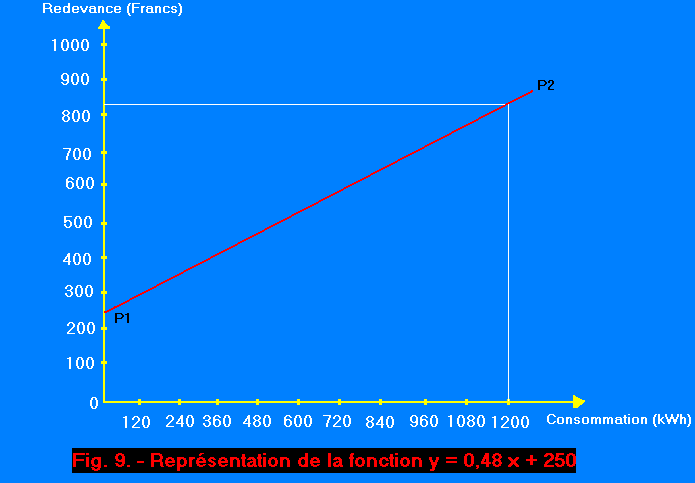
Déterminons les deux points nécessaires au tracé de la droite.
Nous avons y = 0,48 x + 250
Pour x = 0 y = 250 (P1)
Pour y = 0 0 = 0,48 x + 250 - 0,48 x = 250
x = - 250 / 0,48 = - 520
Nous n'avons pas cette valeur sur notre graphique. Nous pourrions la trouver en prolongeant l'axe des x vers les valeurs négatives. Mais faisons autrement. Supposons que notre consommation soit de 1 200 kWh ce qui correspond à une redevance de :
y = 0,48 . 1 200 + 250
y = 826
Nous avons ainsi déterminé les coordonnées du deuxième point : P2 (1 200 , 826). Les deux points étant trouvés, il ne reste plus qu'à tracer la droite.
En électrotechnique ou en électronique, on rencontre des lois dont la forme générale est y = ax + b.
Dans l'étude des transistors, on trouve la relation :
Ic =
![]() IB + ICEO
IB + ICEO
L'analogie avec y = ax + b est évidente
![]() 6. - GRANDEUR
PROPORTIONNELLE AU CARRÉ D'UNE AUTRE GRANDEUR
6. - GRANDEUR
PROPORTIONNELLE AU CARRÉ D'UNE AUTRE GRANDEUR
Définition : Une grandeur est proportionnelle au carré d'une autre quand l'une ayant une valeur, l'autre prend le carré de cette valeur.
Considérons une résistance dans laquelle on fait passer un courant I de différentes valeurs. Un wattmètre branché dans le circuit nous permet de mesurer la puissance P consommée par cette résistance :
|
I |
1 |
2 |
3 |
4 |
5 |
|
P |
10 |
40 |
90 |
160 |
250 |
Établissons maintenant les rapports entre les puissances et le carré des courants correspondants.
10 / 12 = 10 ; 40 / 22 = 40 / 4 = 10 ; 90 / 32 = 90 / 9 = 10 ; 160 / 42 = 160 / 16 = 10 ; 250 / 52 = 250 / 25 = 10
Nous remarquons que ce rapport est constant. La valeur obtenue dans notre exemple (10) est celle de la résistance R.
Nous pouvons donc écrire :
R = P / I2
D'une manière générale, si (x) est la mesure d'une grandeur et (y) la mesure d'une autre grandeur proportionnelle au carré de la première, le rapport de proportionnalité "a" s'exprime par la relation :
a = y / x2 ou y = ax2
La définition du début du paragraphe peut donc s'exprimer ainsi : une grandeur (y) est proportionnelle au carré d'une grandeur (x) quand elles sont liées par la relation : y = ax2, "a" étant un coefficient fixe.
![]() 7. - FONCTION
y = ax2
7. - FONCTION
y = ax2
7. 1. - FONCTION y = x2
Dans le cas où a = 1, la fonction y = ax2 se réduit à y = x2.
Pour étudier graphiquement la fonction y = x2, nous allons donner à x des valeurs quelconques positives et négatives. Chacune de ces valeurs, élevée au carré, donnera la valeur correspondante de y.
Écrivons donc la suite des nombres entiers et en dessous leurs carrés :
|
x = |
- 5 |
- 4 |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
y = x2 = |
25 |
16 |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
16 |
25 |
En examinant ce tableau nous remarquons :
![]() Lorsque les nombres négatifs augmentent, c'est-à-dire
lorsqu'ils se rapprochent de zéro, leurs carrés diminuent,
Lorsque les nombres négatifs augmentent, c'est-à-dire
lorsqu'ils se rapprochent de zéro, leurs carrés diminuent,
![]() Lorsque les nombres positifs augmentent, leurs carrés
augmentent,
Lorsque les nombres positifs augmentent, leurs carrés
augmentent,
![]() Deux nombres opposés ont le même carré.
Deux nombres opposés ont le même carré.
Les résultats obtenus sont représentés graphiquement figure 10 (le procédé pour tracer une courbe étant maintenant supposé connu, nous ne l'expliquerons plus dans le détail).
Nous remarquons que la courbe obtenue n'est plus une droite comme dans le cas de deux grandeurs directement proportionnelles. Cette courbe s'appelle une parabole.
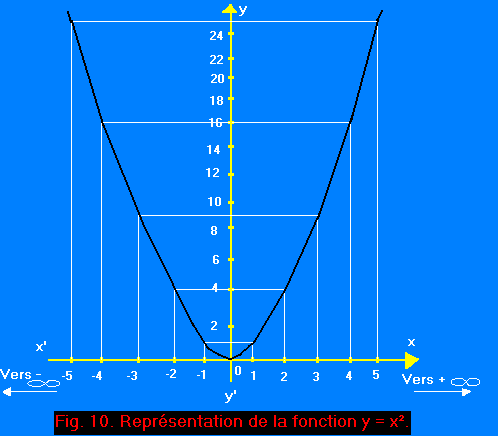
D'autre part, on peut observer que :
-
- La fonction est définie pour toutes les valeurs de x ; autrement dit, quelque soit x (x pouvant varier de -
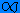 +
+
 ),
on peut toujours calculer son carré x2
;
),
on peut toujours calculer son carré x2
;
-
- La fonction est toujours positive, sauf pour x = 0, valeur pour laquelle y = 0
-
- Quand on donne à x deux valeurs opposées, y prend la même valeur : Si x est égal à - 3 ou à + 3, y = 9 dans les deux cas. Autrement dit, la courbe admet l'axe y'y comme axe de symétrie ;
-
Quand x varie de -
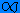 à 0, la fonction est décroissante ; quand x varie de 0 à +
à 0, la fonction est décroissante ; quand x varie de 0 à +
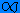 ,
elle est croissante ;
,
elle est croissante ;
-
- La fonction passe par un minimum x = 0 ;
-
Quand x croît indéfiniment par valeurs positives ou négatives, y croît indéfiniment.
L'étude de la variation de la fonction y = x2 peut se résumer par le tableau suivant que nous utiliserons encore par la suite.
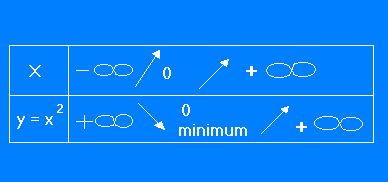
Dans la première ligne de ce tableau, on trouve
différentes valeurs de x. Nous avons pris ici les valeurs extrêmes -
![]() et +
et + ![]() et la valeur zéro. Dans l'étude de fonctions un peu plus compliquées, on
prend d'autres valeurs particulières comme nous le verrons. L'inclinaison des flèches donne le sens de variation des nombres compris entre les deux valeurs
situées de part et d'autre de la flèche lorsque l'on compte de la valeur située
à gauche de celle-ci pour aboutir à celle qui est située à droite. Ainsi,
lorsque l'on part de -
et la valeur zéro. Dans l'étude de fonctions un peu plus compliquées, on
prend d'autres valeurs particulières comme nous le verrons. L'inclinaison des flèches donne le sens de variation des nombres compris entre les deux valeurs
situées de part et d'autre de la flèche lorsque l'on compte de la valeur située
à gauche de celle-ci pour aboutir à celle qui est située à droite. Ainsi,
lorsque l'on part de -
![]() pour arriver à zéro, les valeurs relatives des nombres augmentent au fur
et à mesure que l'on se rapproche de 0 ;
on résume cela par une flèche à laquelle on donne une inclinaison
ascendante. Lorsque l'on part de 0 et que l'on continue indéfiniment à
compter, les valeurs des nombres augmentent également et la flèche est encore
ascendante.
pour arriver à zéro, les valeurs relatives des nombres augmentent au fur
et à mesure que l'on se rapproche de 0 ;
on résume cela par une flèche à laquelle on donne une inclinaison
ascendante. Lorsque l'on part de 0 et que l'on continue indéfiniment à
compter, les valeurs des nombres augmentent également et la flèche est encore
ascendante.
La deuxième ligne donne les valeurs de la
fonction calculées d'après celles de la variable situées dans la première
ligne. Lorsque l'on part de + ![]() pour arriver à zéro, il est évident que les valeurs des nombres sont de
plus en plus petites, d'où la flèche descendante.
pour arriver à zéro, il est évident que les valeurs des nombres sont de
plus en plus petites, d'où la flèche descendante.
Au contraire et comme précédemment, lorsque l'on compte de zéro jusqu'à l'infini, les valeurs augmentent et la flèche est ascendante.
7. 2. - FONCTION y = 2 x2
Cette fonction peut se mettre sous la forme :
y = x2 X 2
Ainsi, pour calculer y, il suffit de multiplier par 2 les valeurs obtenues pour x2.
Faisons ces calculs pour quelques valeurs arbitraires de x, inscrivons les résultats dans le tableau suivant et symbolisons par des flèches, comme nous l'avons vu, le sens des variations.

En analysant le tableau, nous voyons que pour les valeurs de :
- x variant
de -
![]() à 0 : y
décroît de +
à 0 : y
décroît de + ![]() à 0
à 0
- x variant de 0 à +
![]() : y croît de 0
à +
: y croît de 0
à + ![]()
La courbe de la figure 11 matérialise les différents résultats.
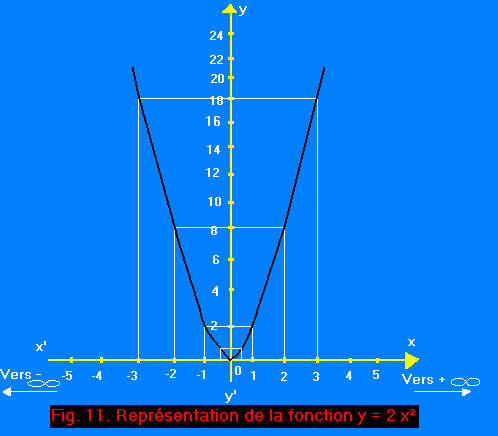
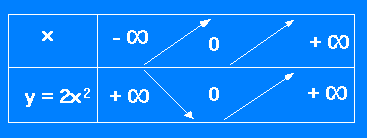
Remarque : On ne porte pas toujours dans les tableaux les calculs et valeurs intermédiaires ayant servis à construire la courbe. Le tableau se simplifie et se présente alors comme celui-ci :
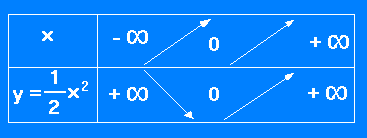
7. 3. - FONCTION y = (1 / 2) x2
Comme précédemment, commençons par dresser le tableau de l'étude des variations de (y) en fonction de celles de x.

Le tableau résumé est le suivant :
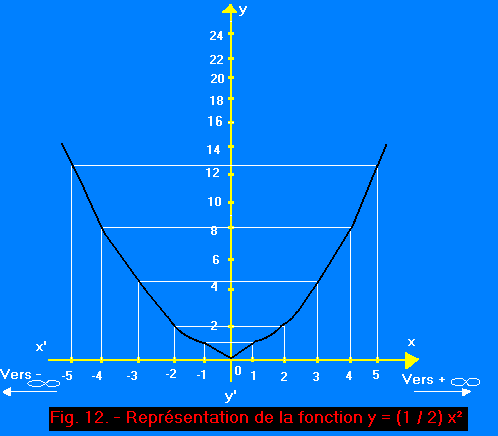
Traçons maintenant la courbe correspondante (figure 12).
Nous voyons que la courbe obtenue est toujours une parabole.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente
|
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.
 Grandeur proportionnelle au carré d'une autre grandeur
Grandeur proportionnelle au carré d'une autre grandeur
