 Rappel sur les coordonnées d'un point Rappel sur les coordonnées d'un point |
 Représentation graphique Représentation graphique |
 Fonction y = ax Fonction y = ax |
 Bas de page Bas de page |
Notion de Fonction - 1ère Partie :
NOTION DE FONCTION "1ère PARTIE"
Ce quatrième leçon de mathématique est consacré à l'examen de quelques fonctions.
Nous verrons tout d'abord ce qu'il faut entendre par le terme "fonction". Cela fait l'objet du premier paragraphe.
Cette notion acquise, nous ferons un rappel sur les coordonnées d'un point. En effet, les fonctions se représentant graphiquement, il est nécessaire pour les tracer, de savoir situer dans un plan quelques-uns de leurs points particuliers. Après avoir revue ce qu'en arithmétique on appelle des grandeurs directement (ou inversement) proportionnelles, nous aborderons dans les autres paragraphes l'examen des fonctions proprement dites.
Comme nous l'avons déjà dit, nos leçons de mathématiques ne constituent pas un cours de mathématiques à proprement parler, mais contiennent les connaissances nécessaire à la bonne compréhension des autres leçons théoriques. C'est la raison pour laquelle les fonctions étudiées sont celles qui sont les plus souvent liées à certaines lois électriques, électrotechniques ou électroniques.
Nous nous sommes efforcés de donner un exemple d'application, soit dans la théorie elle-même, soit des exemples complémentaires. Comme toujours, nous vous invitons à refaire chaque exemple.
1. - NOTION DE FONCTION
Souvent, la loi de dépendance entre deux grandeurs peut être précisée. Ainsi, lorsqu'un piéton marche à la vitesse constante de 6 km / h, la distance parcourue dépend du temps pendant lequel il a marché. Si l'on représente la vitesse par le symbole "v", la distance parcourue par "d", le temps du parcours par "t", on peut écrire :
d = v.t
Sachant que v = 6 et connaissant le temps "t", on peut calculer la distance "d". On dit que la distance est fonction du temps.
Nous savons qu'aux bornes d'une résistance R donnée, la tension U existant à ses bornes dépend de l'intensité I du courant traversant cette résistance. Nous connaissons la relation qui lie ces trois grandeurs :
U = RI
Nous dirons que la tension U est, pour une résistance R donnée, en fonction de l'intensité I du courant. Par définition, on dira :
Une grandeur est une fonction connue d'une autre grandeur quand, connaissant une valeur de la deuxième, on peut calculer la valeur correspondante de la première.
Exemple numérique appliqué à la relation :
U = RI où R = 10 ohms
Si I = 1 ampère U = 10 . 1 = 10 Volts
Si I = 2 ampères U = 10 . 2 = 20 Volts
Si I = 3 ampères U = 10 . 3 = 30 Volts
Généralisons notre formule de la loi d'Ohm sous une forme mathématique.
Comme nous avions convenu que la valeur de la résistance était constante, nous remplaçons la lettre "R" par "a". Tant qu'aux deux autres grandeurs U et I, remplaçons-les respectivement par y et x. La relation U = RI peut alors s'écrire :
y = ax
Ainsi, à chaque valeur de x correspond une valeur de y que l'on sait calculer. On dit encore que le nombre y est en fonction du nombre x.
Lorsqu'un nombre est fonction d'un autre on peut, connaissant l'un, calculer l'autre.
Le nombre x, auquel on donne les valeurs que l'on veut, s'appelle la variable. Le nombre y, que l'on calcule, s'appelle la fonction.
Mathématiquement, pour exprimer qu'une grandeur (y) est fonction d'une variable x, on écrit :
y = f (x)
qui se lit : y égal f de x ou y est une fonction de x.
![]() 2. - RAPPEL
SUR LES COORDONNÉES D'UN POINT
2. - RAPPEL
SUR LES COORDONNÉES D'UN POINT
Traçons deux axes perpendiculaires orientés (on dit aussi rectangulaires) x'Ox et y'Oy (figure 1).
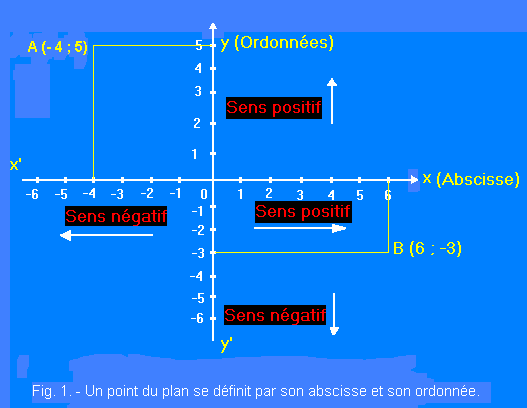
2. 1. - RAPPEL DE DÉFINITIONS
L'axe x'x s'appelle l'axe des abscisses ou axe des x ; l'axe y'y s'appelle l'axe des ordonnées ou axe des y.
L'axe des abscisses et celui des ordonnées forment les axes de coordonnées. Le point 0 est l'origine des coordonnées.
2. 2. - POSITIONNEMENT D'UN POINT PAR RAPPORT A SES COORDONNÉS
A un couple de deux nombres algébriques quelconques, exemple x = - 4 et y = 5, correspond un point A du plan que l'on obtient de la manière suivante :
-
x étant égal à - 4, compter sur x'x, en partant de 0 et dans le sens négatif, 4 graduations ;
-
y étant égal à 5, compter sur y'y, en partant de 0 et dans le sens positif, 5 graduations ;
-
par les deux graduations repérées, mener les parallèles aux axes ; elles se coupent au point A.
On dit que les nombres - 4 et + 5 sont les coordonnées du point A ; - 4 est son abscisse, + 5 est son ordonnée.
2. 3. - DÉFINITION DES COORDONNÉES D'UN POINT SITUÉ DANS LE PLAN
Soit un point B (figure 1) situé dans le plan.
Par ce point, on même les parallèles aux axes des coordonnées. L'intersection de ces parallèles avec les différents axes détermine les coordonnées du point.
Ainsi, figure 1, le point B a pour coordonnées x = 6 et y = - 3, ce qui s'écrit : B (6,- 3).
2. 4. - ÉCHELLE DES GRADUATIONS
Pour simplifier, nous avons porté des divisions ayant même longueur sur les deux axes. Cependant, on peut porter sur l'un des axes des divisions de longueur différente de celle portée sur l'autre, c'est-à-dire adopter des échelles différentes pour les deux graduations.
Par exemple, reprenons la représentation de la loi d'OHM que nous avons vue dans la leçon précédente.
Soit le circuit de la figure 2-a. Un générateur débite dans une résistance fixe de 100 ohms. Si la tension fournie par le générateur prend successivement les valeurs de 100, 200, 300...volts, le courant correspondant aura pour valeur 1, 2, 3... ampères (application de la relation I = U / R).
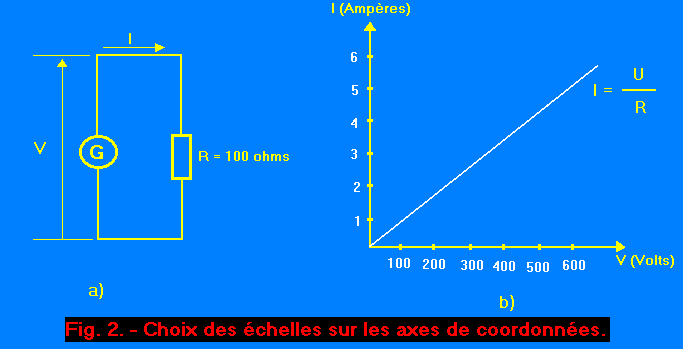
L'ampère et le volt sont deux unités correspondantes. Si l'on adopte pour échelle 1 cm = 1 ampère, il serait déraisonnable de prendre 1 cm = 1 volt car cela imposerait un graphique de plusieurs mètres (100 V = 100 cm = 1 m, 200 V = 200 cm = 2 m, etc.). En conséquence, pour représenter graphiquement cette relation, on adoptera comme échelle 1 cm = 100 volts et 1 cm = 1 ampère. De plus, sur un même axe, on peut trouver deux échelles différentes.
Prenons l'exemple où nous devons mesurer l'intensité du courant traversant un récepteur R en fonction de la valeur et des polarités de la tension appliquée à ses bornes (le courant est la fonction, la tension la variable). Soit le montage de la figure 3-a.
Supposons que les mesures de la tension U donnent des valeurs de quelques volts et que l'on relève les valeurs correspondantes du courant I1 de l'ordre du milliampère.
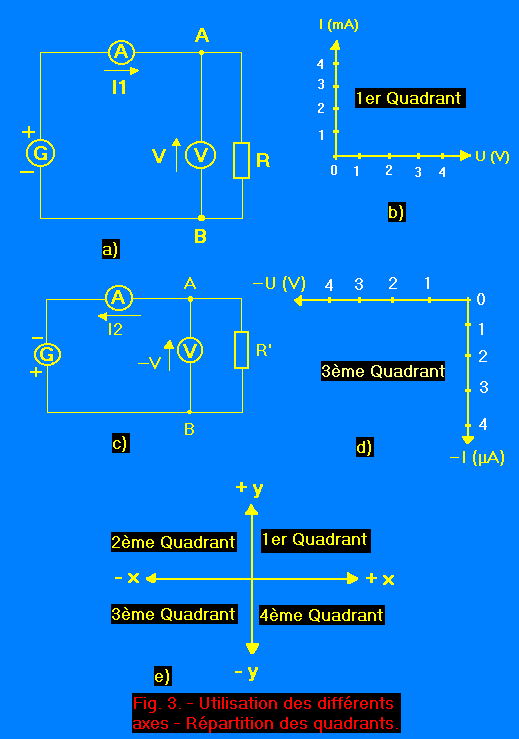
Nous renseignons le graphique figure 3-b en reportant les tensions sur l'axe des x positifs (1 cm = 1 V) et les intensités sur l'axe des y positifs (1 cm = 1 mA).
Modifions le montage comme l'indique la figure 3-c par l'inversion des polarités du générateur et l'augmentation importante de la valeur de la résistance que l'on appellera R'.
Comme précédemment, on mesure toujours des tensions de quelques volts mais les polarités sont inversées. Si l'on convient par exemple de prendre le point B comme potentiel de référence, le point A est devenu négatif par rapport à ce point B. Nous avons donc des tensions négatives et leurs valeurs sont à reporter sur l'axe des x négatifs avec la même échelle, 1 cm = 1 volt.
On mesure les intensités correspondantes du courant I2 qui sont cette fois de quelques microampères et d'un sens contraire à celui de I1. Nous reportons donc ces valeurs sur l'axe des y négatifs et l'on adopte comme échelle 1 cm = 1 µA, c'est-à-dire une échelle 1 000 fois plus grande que précédemment. Nous avons ainsi :
-
en fonction des valeurs à mesurer, choisi des échelles ;
-
en fonction du signe des grandeurs considérées, employé les quadrants correspondants, en l'occurrence le premier et le troisième (Figure 3-e).
![]() 3. - REPRÉSENTATION
GRAPHIQUE DE GRANDEURS DIRECTEMENT PROPORTIONNELLES
3. - REPRÉSENTATION
GRAPHIQUE DE GRANDEURS DIRECTEMENT PROPORTIONNELLES
Définition : Deux grandeurs sont directement proportionnelles quand les diverses valeurs de l'une sont proportionnelles aux valeurs correspondantes de l'autre.
Nous avons vu par exemple que la distance parcourue par un piéton marchant à une vitesse constante dépendait du temps pendant lequel il marchait : la distance parcourue est proportionnelle au temps de marche. De même, l'intensité du courant traversant un récepteur de résistance déterminée, dépend de la tension appliquée aux bornes de ce récepteur. Faisons une application numérique de ce dernier exemple.
Soit un récepteur de résistance de 10 ohms aux bornes duquel on applique une tension qui prendra successivement les valeurs de 10 V, 20 V, 30 V, etc... l'intensité le traversant prendra respectivement les valeurs de 1 A, 2 A, 3 A, etc... puisque I = U / R.
La tension et l'intensité sont donc deux grandeurs directement proportionnelles car, lorsque les valeurs de la tension sont multipliées par 2, 3, 4, etc... les valeurs de l'intensité sont également multipliées par 2, 3, 4, etc...
On remarque que le quotient de deux valeurs correspondantes des grandeurs considérées est constant. On a en effet :
(10 / 1) = (20 / 2) = (30 / 3) etc... = 10
Ce quotient (10 dans notre exemple) est appelé coefficient de proportionnalité. Plus généralement, "y" et "x" étant les mesures correspondantes de deux grandeurs proportionnelles, "a" le coefficient de proportionnalité, ces mesures sont liées par la relation :
y / x = a d'où l'on tire : y = ax
Autrement dit, deux grandeurs sont directement proportionnelles lorsque la mesure de l'une "y" s'obtient en multipliant la mesure correspondante de l'autre "x" par un nombre constant, appelé coefficient de proportionnalité.
![]() 4. - FONCTION
y = ax
4. - FONCTION
y = ax
4. 1. - REPRÉSENTATION GRAPHIQUE
Reprenons notre récepteur de 10 ohms de résistance et faisons-le parcourir par un courant auquel nous donnerons des valeurs arbitraires. Calculons les différentes valeurs correspondantes de la tension que l'on représentera graphiquement.
La tension aux bornes du récepteur est donnée par la relation :
U = RI qui est de la forme y = ax
Nous pouvons donc écrire les équivalences suivantes :
U = y = la fonction
R = 10 = le coefficient de proportionnalité
I = x = la variable
Donnons à x (Donc I) différentes valeurs et calculons les valeurs correspondantes de y (donc U).
|
Valeurs arbitraires de x (I) |
1 |
2 |
3 |
4 |
5 |
|
Valeurs calculées de y (U = RI) |
10 |
20 |
30 |
40 |
50 |
Traçons deux axes de coordonnées, 0x et 0y (figure 4).
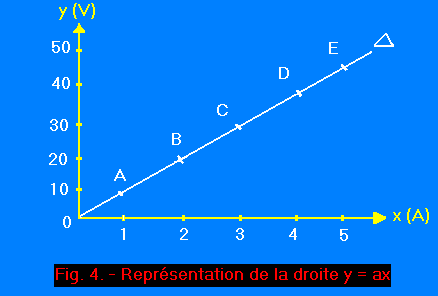
Graduons comme il se doit 0x en ampères et 0y en volts en adoptant comme échelle 1 A = 1 cm et 10 V = 1 cm. Plaçons les points A (1,10) ; B (2,20) ; C (3,30) ; D (4,40) ; E (5,50).
On constate que ces points sont sur une même
droite ![]() (delta)
qui passe par l'origine 0 et que l'on appelle droite représentative de la fonction y = 10 x
d'où la règle :
(delta)
qui passe par l'origine 0 et que l'on appelle droite représentative de la fonction y = 10 x
d'où la règle :
La courbe représentative de la fonction y = ax est une droite passant par l'origine.
Nous rappelons qu'en mathématiques, le mot "courbe" est synonyme de "ligne". Ne soyez donc pas choqué si l'on vous dit qu'une "courbe" est une "droite".
4. 2. - TRACÉ PRATIQUE DE LA DROITE REPRÉSENTANT LA FONCTION y = ax
Comme nous venons de le voir, la droite y = ax passe par l'origine 0.
Comme pour positionner une droite, il suffit de connaître deux de ses points, il nous reste à déterminer un deuxième point, le premier étant connu (l'origine 0). On prend alors une valeur arbitraire de x que l'on multiplie par le coefficient de proportionnalité. Le produit obtenu nous donne l'ordonnée du deuxième point, l'abscisse étant évidemment la valeur arbitraire de x choisie.
En conservant les données précédentes, on prend par exemple x = 4 d'où y = 10 x 4 = 40 et l'on obtient le point P1 (4,40) (figure 5).
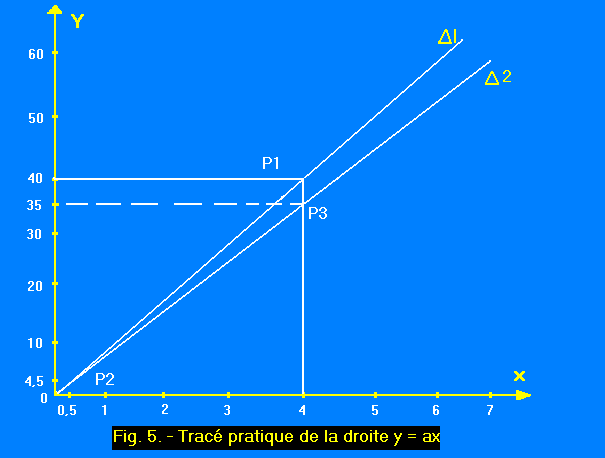
On joint ensuite le point 0 au point P1 et l'on
obtient la droite ![]() 1
qui est la droite de la fonction y = 10 x.
1
qui est la droite de la fonction y = 10 x.
Remarque : Pour la précision du dessin, il est conseillé de prendre une valeur de x la plus grande possible, compatible avec la grandeur du graphique.
Si nous avions choisi pour x la valeur
arbitraire : 0,5 nous aurions obtenu le point P2 (0,5 ; 7).
Il suffit d'une légère erreur de positionnement de ce point pour que les renseignements donnés par la lecture de la courbe soient faux. Ainsi, si nous
repérons P2 (figure 5) non pas avec ses coordonnées exactes (0,5 ; 7)
mais avec une légère erreur (0,5 ; 6,5 environ), pour les valeurs supérieures
de x, l'erreur absolue devient importante. En ayant tracé la droite ![]() 2
nous voyons qu'à la valeur de x = 4 ne correspond plus y = 40 mais
35. L'erreur qui correspond à un écart de 12,5 % n'est pas négligeable.
2
nous voyons qu'à la valeur de x = 4 ne correspond plus y = 40 mais
35. L'erreur qui correspond à un écart de 12,5 % n'est pas négligeable.
4. 3. - GÉNÉRALISATION
Représentons sur un même graphique (figure 6) les fonctions y = ax suivantes :
|
y = - 4x |
y = - x |
y = - 0,5x |
y = 0,5x |
y = x |
y = 3x |
Pour tracer les droites correspondantes, nous devons déterminer deux points : l'un est déjà formé par l'intersection des axes x'x et y'y, c'est le point 0.

Pour obtenir le second, donnons à x une valeur numérique :
|
y = - 4x |
pour x = 2 |
y = - 4 (2) = - 8 = P1 |
|
y = - x |
pour x = 5 |
y = 1 (- 5) = - 5 = P2 |
|
y = - 0,5x |
pour x = 6 |
y = - 0,5 (6) = - 3 = P3 |
|
y = 0,5x |
pour x = 6 |
y = 0,5 (6) = 3 = P4 |
|
y = x |
pour x = 6 |
y = 1 (6) = 6 = P5 |
|
y = 3x |
pour x = 2 |
y = 3 (2) = 6 = P6 |
Ces points étant maintenant parfaitement définis par leurs coordonnées, P1 (2 ; - 8) ; P2 (5 ; - 5) ; P3 (6 ; - 3) etc... nous pouvons les placer dans le plan et tracer les droites représentant chaque fonction en les faisant passer par l'origine 0 et les points P correspondants (figure 6).
Observons la figure 6. Nous remarquons que dans la fonction y = ax :
1 - Lorsque le coefficient "a" est positif (a > 0) ;
- la droite se trouve dans le premier et le troisième quadrant,
- lorsque x croît, y croît aussi : x et y varient dans le même sens.
On dit alors que la fonction est croissante.
2 - Lorsque le coefficient "a" est négatif (a < 0) :
- la droite se trouve dans le deuxième et le quatrième quadrant,
- lorsque x croît, y croît (x et y varient en sens inverse).
On dit alors que la fonction est décroissante.
En résumé, la fonction y = ax est croissante pour a > 0 et décroissante pour a < 0.
4. 4. - PENTE DE LA DROITE y = ax
En continuant d'observer la figure 6, nous faisons la constatation suivante : lorsque le coefficient "a" augmente en valeur absolue, l'angle formé par l'axe des abscisses (x'x) et la droite correspondante augmente également. Ainsi, l'angle x 0 P6 (fonction y = 3 x) est supérieur à l'angle x 0 P5 (fonction y = x).
Le coefficient "a" de "x" dans la relation y = ax s'appelle pente ou coefficient angulaire, de la droite y = ax.
En résumé, la pente de la droite y = ax augmente comme la valeur absolue du coefficient a de x.
Remarque : On démontre en trigonométrie que "a" est la tangente de l'angle formé par l'axe des abscisses avec la droite de la fonction considérée.
Si ![]() désigne cet angle, on a la relation :
désigne cet angle, on a la relation :
a = tg ![]() (tg = tangente).
(tg = tangente).
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente
|
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.

