Convertisseur Digital / Analogique à Amplificateur Opérationnel Convertisseur Digital / Analogique à Amplificateur Opérationnel |
 La Précision des Convertisseurs La Précision des Convertisseurs |
 Bas de page Bas de page |
Amplificateurs Opérationnels - Convertisseur Digital / Analogique à Amplificateur Opérationnel :
2. 2. - AMPLIFICATEURS OPÉRATIONNELS
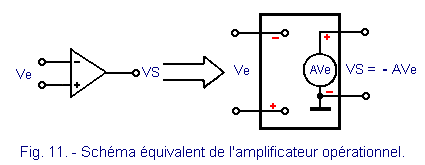
Le symbole graphique de l'amplificateur est donné figure 10.
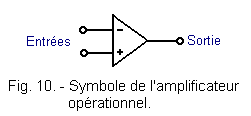
On remarque que l'alimentation n'est pas représentée. Toutefois, sur les circuits, elle est obligatoirement présente. Généralement, on utilise une alimentation symétrique caractérisée par la présence de trois bornes : une pour la tension positive, une pour la tension négative, une pour la masse.
L'amplificateur opérationnel idéal présente les caractéristiques suivantes :
![]() Amplificateur infinie :
l'amplification en tension qui est le rapport entre la tension de sortie VS
et la tension d'entrée Ve (figure 11) peut
être considérée pratiquement infinie :
Amplificateur infinie :
l'amplification en tension qui est le rapport entre la tension de sortie VS
et la tension d'entrée Ve (figure 11) peut
être considérée pratiquement infinie : ![]()
![]() Impédance d'entrée
infinie : avec une impédance d'entrée infinie, l'amplificateur ne
représente pas une charge pour le circuit précédent ; autrement dit,
il n'absorbe aucun courant.
Impédance d'entrée
infinie : avec une impédance d'entrée infinie, l'amplificateur ne
représente pas une charge pour le circuit précédent ; autrement dit,
il n'absorbe aucun courant.
![]() Impédance de sortie nulle
: avec une impédance de sortie idéale nulle, l'amplificateur opérationnel
peut fournir tout le courant requis par la charge, sans influence sur la tension de sortie.
Impédance de sortie nulle
: avec une impédance de sortie idéale nulle, l'amplificateur opérationnel
peut fournir tout le courant requis par la charge, sans influence sur la tension de sortie.
![]() Tension de sortie nulle pour une
tension d'entrée nulle.
Tension de sortie nulle pour une
tension d'entrée nulle.
Dans ce cas, on dit que «l'Offset» est nul. Offset est un terme anglais, utilisé pour indiquer le décalage du point de repos par rapport au zéro.
Avec l'amplificateur opérationnel, il suffit d'une tension d'entrée extrêmement faible pour porter la tension de sortie à une valeur très élevée, très proche de la tension d'alimentation.
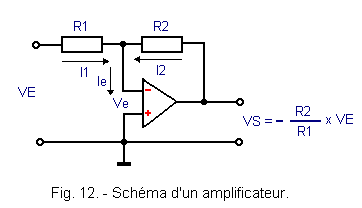
Dans la plupart des cas, il est nécessaire de diminuer le gain de l'ensemble en ajoutant quelques composants. A titre d'exemple, nous allons considérer le montage indiqué figure 12.
Dans ce circuit, on a ajouté deux résistances R1 et R2. R2 assure une contre-réaction entre la sortie et l'entrée inverseuse de l'amplificateur opérationnel.
Dans l'amplificateur idéal, l'impédance d'entrée est infinie, donc le courant d'entrée est nul.
Le courant d'entrée Ie correspond également à la somme des courants traversant R1 et R2.
I1 + I2 = Ie = 0
On en déduit que :
I2 = - I1
Les courants I2 et I1 peuvent également s'exprimer de la façon suivante :
.gif)
Comme le courant d'entrée est nul, on peut considérer que la tension Ve aux bornes de l'impédance d'entrée l'est également.
L'équation précédente devient :
.gif)
On en déduit donc que l'amplification A du montage est égale au rapport des résistances R2 et R1 et ne dépend plus de l'amplification de l'amplificateur opérationnel. Cette dernière a été considérée infinie. En réalité, elle ne l'est pas, mais sa valeur est tellement élevée (plus de 105) que l'on peut appliquer la formule VS / VE = - R2 / R1 en toute tranquillité.
Le signe «-» placé devant le rapport des résistances R1 et R2, indique que la tension de sortie VS est de signe opposé (ou en opposition de phase) avec VE.
Une autre utilisation de l'amplificateur opérationnel est illustrée figure 13.
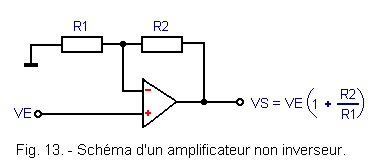
La tension d'entrée VE est appliquée directement à la borne + (entrée non inverseuse). Le réseau de réaction identique au circuit précédent est constitué par les résistances R1 et R2.
Dans ce type de configuration, la formule qui exprime la tension de sortie est :
![]()
![]() 2. 3. -
CONVERTISSEUR
DIGITAL / ANALOGIQUE A AMPLIFICATEUR OPÉRATIONNEL
2. 3. -
CONVERTISSEUR
DIGITAL / ANALOGIQUE A AMPLIFICATEUR OPÉRATIONNEL
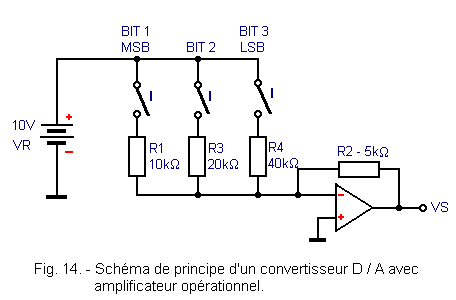
Le principe d'un convertisseur digital / analogique à 3 bits utilisant un amplificateur opérationnel est illustré figure 14.
Les contacts des interrupteurs peuvent être mécaniques ou électroniques. Quand le bit vaut 0, l'interrupteur est ouvert, quand il prend la valeur 1, l'interrupteur est fermé.
Voyons maintenant ce qui se passe avec un nombre binaire égal à 100. Le premier contact est fermé, les deux autres sont ouverts, comme indiqué figure 15.
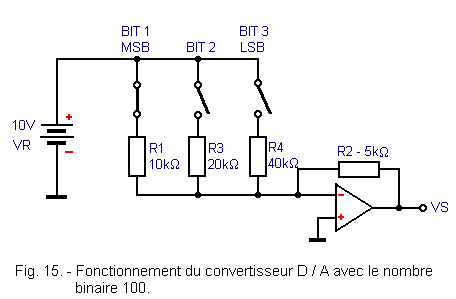
En comparant cette figure avec la figure 12, on constate que les deux circuits sont équivalents car les deux résistances R3 et R4 n'ont aucune influence.
La tension de sortie VS est égale à :
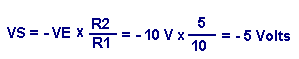
Elle correspond à la moitié de la tension d'entrée. Si on ferme uniquement le deuxième interrupteur (nombre 010), on obtient une tension de sortie de :
.gif)
Dans ce cas, la tension de sortie correspond au quart de la tension d'entrée.
Si enfin, on ferme uniquement le troisième interrupteur (nombre binaire 001), la tension de sortie devient :
.gif)
Soit une tension égale au huitième de la tension d'entrée.
Pour obtenir une tension VS égale à 1 / 16 de la tension d'entrée, il faudrait utiliser un quatrième interrupteur et une résistance de 80 kW.
Si plusieurs contacts sont fermés, la tension de sortie est obtenue en additionnant les tensions correspondant à chacun des interrupteurs pris séparément.
Ainsi, pour la combinaison 101, on a :
VS = - (1 / 2 + 1 / 8) x VE = - 5 / 8 x 10V = - 6,25 Volts.
En pratique, le circuit tel que nous venons de le décrire, n'est pas utilisé. En effet, si l'on voulait travailler avec 12 bits par exemple, la valeur de la dernière résistance serait égale à 20,480 MW.
Il est assez difficile de réaliser des résistances de très grande valeur avec une bonne précision.
D'autre part, du fait des grandes différences de valeurs, les variations des résistances dues à la température ne sont pas identiques. Le poids de chacun des bits (1 / 2, 1 / 4, 1 / 8, etc...) n'est plus exact et la précision du système est mauvaise.
2. 4. - RÉSEAU DE RÉSISTANCES (R - 2R)
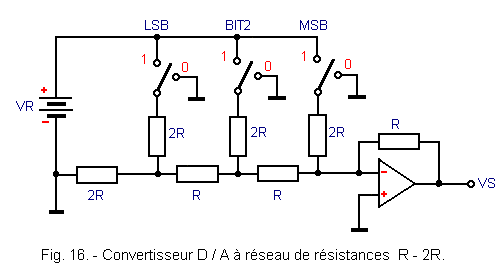
La solution adoptée pour surmonter les problèmes créés par des résistances de valeurs trop différentes est représentée figure 16.
Elle consiste à utiliser uniquement deux valeurs de résistances : R et 2R.Dans ce circuit, les interrupteurs relient les résistances 2R, soit vers la tension de référence VR, soit vers la masse, selon que le bit correspondant est à 1 ou à 0.
Le bit de poids fort (MSB) est situé à droite du réseau de résistances R - 2R. Lorsque l'interrupteur correspondant à ce bit est sur la position 1, la tension de sortie est égale à :
![]()
Avec les calculs traditionnels sur les ponts diviseurs de tensions (qui ne sont pas effectués ici), on démontre que le poids de chacun des bits est de 1 / 2, 1 / 4, 1 / 8, etc...
Si le bit 2 est par exemple à 1, le circuit devient celui indiqué figure 17.
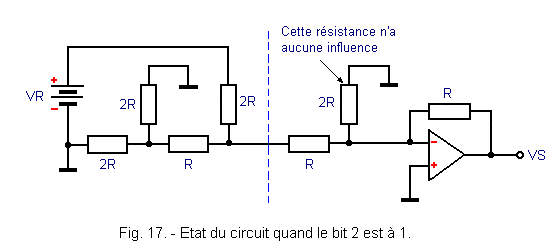
La résistance 2R, correspondant au bit MSB, n'a aucune influence, car elle est connectée entre la masse et l'entrée de l'amplificateur opérationnel qui constitue une masse virtuelle (potentiel très proche de 0 V).
Le réseau de résistances situé à gauche du trait en pointillé peut se résumer à celui indiqué figure 18-a.
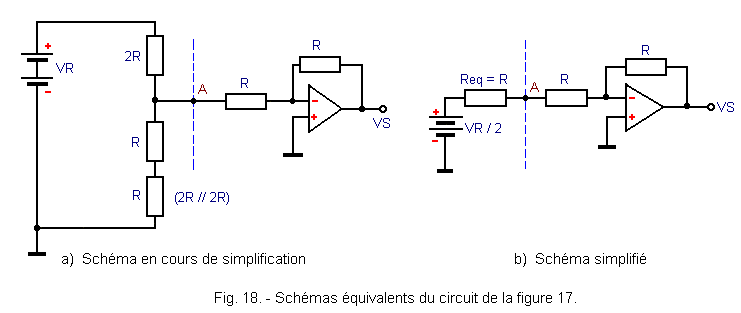
D'après le théorème de THEVENIN, le réseau situé entre le point A et la masse peut être remplacé par un circuit constitué d'un générateur en série avec une résistance équivalente Req.
![]() Le générateur a comme tension la valeur mesurée à vide entre le point A
et la masse : ici, on obtient VR / 2
puisque le point A est relié au milieu de
la chaîne de résistances connectées aux bornes de la tension VR.
Le générateur a comme tension la valeur mesurée à vide entre le point A
et la masse : ici, on obtient VR / 2
puisque le point A est relié au milieu de
la chaîne de résistances connectées aux bornes de la tension VR.
![]() La résistance équivalente Req
est égale
à la résistance vue entre le point A et la masse lorsque l'on remplace le générateur de tension
VR
par un court-circuit.
La résistance équivalente Req
est égale
à la résistance vue entre le point A et la masse lorsque l'on remplace le générateur de tension
VR
par un court-circuit.
On obtient ici deux résistances de 2R en parallèle, soit Req = R.
Finalement, le montage des figures 17 et 18-a se résume à celui de la figure 18-b.
A l'aide de cette figure 18-b simplifiée, on constate que la tension de sortie est égale à :
![]()
Le poids du bit N° 2 est donc de 1 / 4 de VR.
Une solution intermédiaire entre le réseau de résistances de la figure 14 et celui de la figure 16 est représenté figure 19.
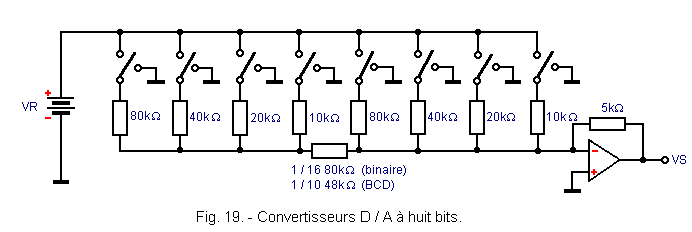
Dans ce circuit, on utilise deux groupes de résistances dont chacune est le double de la précédente.
Entre les deux groupes de résistances, on insère une résistance de valeur appropriée de façon à provoquer soit une atténuation de 1 / 16 si l'on effectue une conversion en binaire pur, soit une atténuation de 1 / 10 si l'on travaille en code BCD.
2. 5. - CONVERTISSEURS "D / A" À CIRCUITS INTÉGRÉS
Les convertisseurs D / A sont actuellement disponibles sous forme de circuits intégrés. Les convertisseurs ainsi réalisés atteignent une précision de l'ordre de 0,05 % à 0,0125 %.
Sur le marché, on rencontre plusieurs types de convertisseurs D / A intégrés, le plus simple est représenté figure 20.
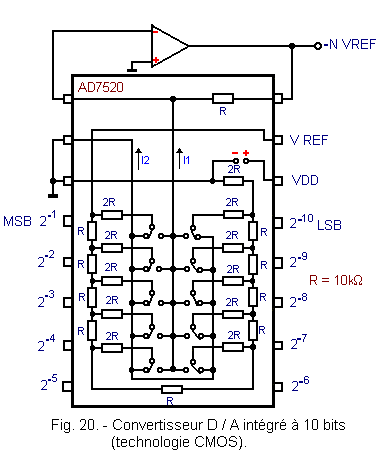
On reconnaît le réseau de résistances R - 2R et les dix interrupteurs qui, bien entendu, sont réalisés avec des transistors à effet de champ.
Un autre circuit plus complexe est représenté figure 21.
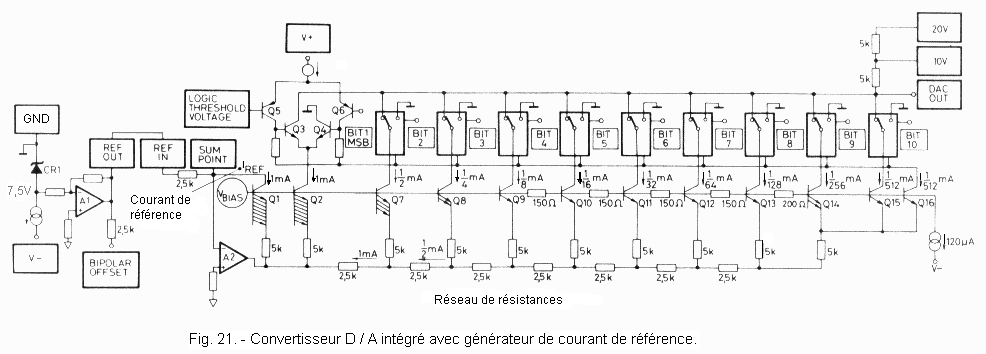
Ce convertisseur utilise un réseau de résistances R - 2R dont chaque branche est alimentée par un générateur de courant (1 mA, 1 / 2 mA, 1 / 4 mA, 1 / 8 mA, etc...).
Dans les deux cas, l'utilisateur doit ajouter l'amplificateur opérationnel qui n'est pas incorporé dans le boîtier. Le choix de l'amplificateur sera en fonction de la vitesse de commutation requise.
La sortie du réseau de résistances peut être reliée à l'entrée «-» ou à l'entrée «+» de l'amplificateur et selon le cas, on obtient en sortie une tension négative ou positive.
Si l'on utilise le convertisseur représenté figure 21, qui délivre en fait un courant I proportionnel au nombre binaire d'entrée, on peut réaliser deux branchements différents (figure 22-a et 22-b).
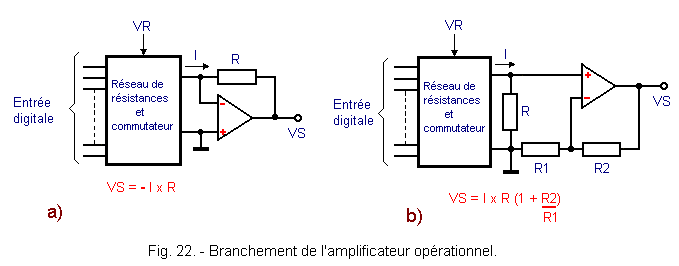
Le courant I provenant du réseau de résistances dépend du signal digital et de la tension de référence VR.
Généralement, on préfère la configuration de la figure 22-a, car elle procure une plus grande précision.
![]() 2. 6. - LA PRÉCISION DES
CONVERTISSEURS
2. 6. - LA PRÉCISION DES
CONVERTISSEURS
Les deux principales caractéristiques d'un convertisseur D / A sont : la résolution et la précision.
Comme nous l'avons vu précédemment, la résolution dépend du nombre de bits d'entrée que peut traiter le circuit. Ce nombre détermine en combien d'échelons peut être divisée la tension de référence VR.
La figure 23 donne la relation entre l'entrée digitale et la sortie analogique d'un convertisseur idéal à 3 bits.
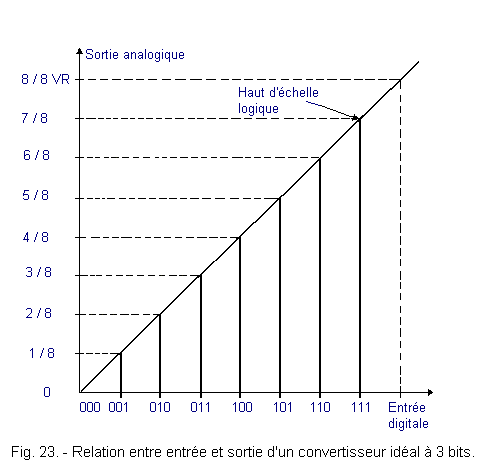
La résolution de ce circuit correspond à l'accroissement de la tension analogique de sortie, provoquée par l'augmentation d'une unité du nombre binaire d'entrée.
Dans ce cas précis, la résolution est de 1 / 8 de VR. Pour un circuit à 4 bits, elle serait de 1 / 16 de VR.
A chaque combinaison binaire d'entrée, correspond une tension de sortie. Par exemple, le nombre binaire 100 détermine une tension de sortie égale à 0,5 VR. En réalité, cette valeur est légèrement différente, elle peut être de 0,49 VR ou de 0,51 VR. L'écart entre la valeur idéale et celle obtenue réellement (± 0,01 VR, c'est-à-dire 1 % par excès ou par défaut) est appelé degré de précision ou simplement précision.
Il ne faut pas confondre résolution et précision. En effet, on rencontre des convertisseurs à faible résolution, par exemple à 3 bits, donnant 8 niveaux, mais avec une très grande précision. A l'inverse, il existe des circuits à haute résolution (10 à 12 bits d'entrée), mais dont la précision est médiocre.
Les facteurs affectant la précision des convertisseurs peuvent être très divers comme nous allons le voir à présent.
2. 6. 1. - OFFSET NON NUL
Lorsque tous les bits d'entrée sont à 0, on devrait obtenir 0 volt en sortie. Ce n'est pas toujours le cas et l'on parle alors d'erreur ou de décalage d'offset. Cet écart est constant et existe pour toutes les valeurs binaires d'entrée, comme le montre la figure 24.
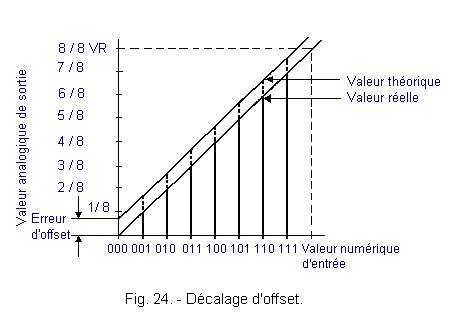
2. 6. 2. - ERREUR DE TRANSFERT
Ce défaut apparaît lorsque le gain de l'amplificateur est excessif ou trop faible. On obtient alors des valeurs de tensions analogiques plus hautes ou plus basses que celles prévues. La figure 25 montre le décalage entre les valeurs réelles obtenues et les valeurs idéales. On constate que l'erreur est d'autant plus grande que la valeur numérique d'entrée est élevée.
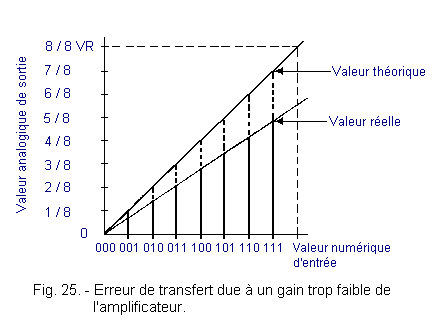
2. 6. 3. - ERREUR DUE A LA NON - LINÉARITÉ
Une cause importante de l'imprécision est la mauvaise linéarité du système. Celle-ci est due en grande partie aux réseaux de résistances.
La précision d'un convertisseur dépend de la valeur absolue de chacune des résistances et des rapports existant entre les différentes résistances mises en service. Il est très important que ces rapports soient maintenus dans tout le champ de travail.
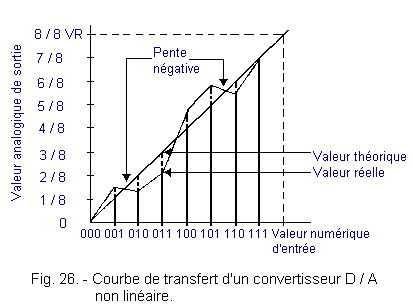
La figure 26 montre l'allure que pourrait prendre la courbe de transfert d'un convertisseur D / A à 3 bits de très mauvaise qualité.
Il est bien évident qu'un tel convertisseur est inutilisable.
Il est inévitable que la valeur des résistances varies avec la température. Pour cette raison, on utilise toujours des réseaux de résistances intégrés dans des microcircuits ; en effet, avec cette technologie, les résistances sont toutes réalisées avec le même matériau ; de plus, elles sont très proches et donc subissent les mêmes variations de température.
En termes généraux, la précision révèle de combien un convertisseur s'écarte du comportement théorique.
Généralement, sur les notices constructeurs, on rencontre deux types de précision : précision absolue et précision relative.
La précision absolue est l'écart entre la sortie analogique que l'on désire quand on applique un code binaire en entrée, et la sortie réellement obtenue.
Pour corriger cet écart, on peut intervenir sur le gain de l'amplificateur opérationnel ou sur la tension de référence VR.
La précision
relative est obtenue en faisant le rapport entre l'écart et la
valeur théorique que l'on devrait obtenir.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente |
 Page suivante Page suivante |
Nombre de pages vues, à partir de cette date : le 15 JUILLET 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.