Le signe de l'opérateur, placé
devant ces parenthèses, peut, selon l'opération, modifier le signe relatif
attribué à la valeur numérique absolue, de la façon suivante :
 Si les parenthèses sont précédées du signe de la somme (+ : plus), le signe de la valeur
absolue contenue entre ces parenthèses n'est pas modifié.
Si les parenthèses sont précédées du signe de la somme (+ : plus), le signe de la valeur
absolue contenue entre ces parenthèses n'est pas modifié.
Exemple :

 Si les parenthèses sont précédées du signe de la différence (-
; moins), le signe de la valeur absolue contenue entre ces parenthèses, doit être changé.
Si les parenthèses sont précédées du signe de la différence (-
; moins), le signe de la valeur absolue contenue entre ces parenthèses, doit être changé.
Exemple :
 Dans le cas du produit de deux nombres relatifs, la valeur absolue du résultat
est positive (+) si les deux nombres sont de
même signe.
Dans le cas du produit de deux nombres relatifs, la valeur absolue du résultat
est positive (+) si les deux nombres sont de
même signe.
Exemple :
-
(+ 5) x (+ 5) = (+ 25)
-
(- 5) x (- 5) = (+ 25)
 La valeur absolue du produit de deux nombres relatifs est négative, si ces deux
nombres sont de signes contraire.
La valeur absolue du produit de deux nombres relatifs est négative, si ces deux
nombres sont de signes contraire.
Exemple :
 La valeur absolue du quotient de deux nombres relatifs est positive, si les deux
nombres sont de mêmes signes.
La valeur absolue du quotient de deux nombres relatifs est positive, si les deux
nombres sont de mêmes signes.
Exemple :
-
(+ 12) / (+ 3) = (+ 4)
-
(- 12) / ( - 3) = (+ 4)
Le quotient peut aussi se noter de la façon suivante :
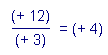
L'écriture sur une seule ligne avec la barre inclinée, symbole
du quotient, est une notation plus commode du point de vue dactylographique.
 La valeur absolue du quotient de deux nombres relatifs, est négative, si ces
deux nombres sont de signes contraires.
La valeur absolue du quotient de deux nombres relatifs, est négative, si ces
deux nombres sont de signes contraires.
Exemple :
-
(+ 12) / (- 3) = (- 4)
-
(- 12) / (+ 3) = (- 4)
 5. 1. - L'ADDITION DÉCIMALE
5. 1. - L'ADDITION DÉCIMALE
En règle générale, pour l'addition ou pour la soustraction,
on inscrit le premier terme, puis en dessous, le ou les termes suivants, en plaçant
dans les mêmes colonnes les chiffres affectés à des poids identiques.
Pour l'addition, plus de deux termes peuvent être disposés les
uns en dessous des autres.
Nous additionnerons ensuite les chiffres de la colonne la plus
à droite (de poids le plus faible).
Dans le système décimal, tout résultat supérieur à 9 génère
un report dans la colonne suivante de poids immédiatement supérieur.
On additionne ensuite les chiffres alignés dans la seconde
colonne, plus le report s'il existe et ainsi de suite jusqu'à la dernière colonne occupée.
On positionne, dans le rang de poids supérieur, le report de la
dernière colonne, s'il y en a un.
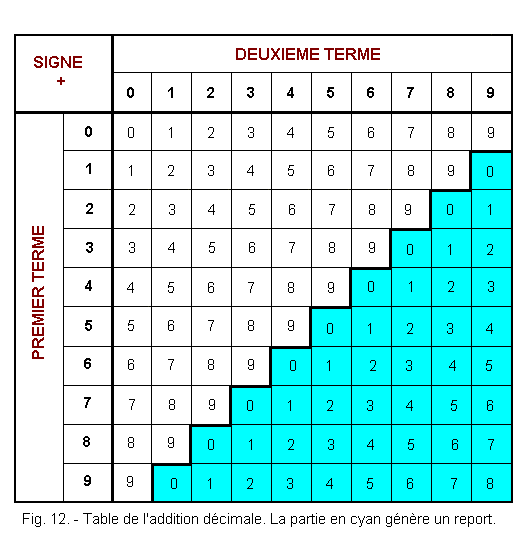
La figure 12 représente la table de l'addition décimale. On désigne
le premier terme (à gauche des lignes et en caractères gras), puis le second terme (en caractères gras, colonne supérieure). Le résultat est donné dans
la case se trouvant à l'intersection de la ligne et de la colonne correspondant
aux termes choisis. dans la partie en cyan, la somme des termes 1 et 2
impose un report dans la colonne de poids supérieur.
Le résultat de cette opération est un total.
Exemple : Soit à additionner 75 et 46 : la figure 13 donne la procédure.
.gif)
La somme ou addition ne se limite pas aux nombres positifs,
comme nous l'avons vu au début de ce chapitre, mais à l'ensemble des nombres relatifs.
D'une manière générale, elle donne pour résultat la somme
des valeurs absolues quand les nombres sont de même signe et la différence s'ils sont de signes contraires.
Le signe du résultat est le même que celui des deux nombres
qui a la plus grande valeur absolue.
Exemple :
 5. 2. - L'ADDITION BINAIRE
(Retour)
5. 2. - L'ADDITION BINAIRE
(Retour)
Elle s'effectue de la même manière que l'addition décimale.
La numération étant à base 2,
tout résultat supérieur à 1 génère un
report dans la colonne suivante.
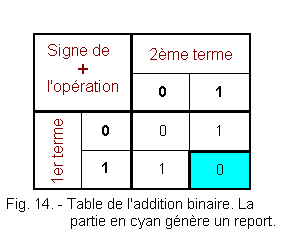
La figure 14 représente la table de l'addition binaire.
L'utilisation de cette table s'effectue de la même manière que pour celle de l'addition décimale de la figure 12. Dans la partie en
cyan, la somme des termes 1 et 2 génère un report. On notera la grande simplicité de cette table par rapport
à celle de l'addition décimale.
Exemple : Soit à additionner
1310
et 510.
Effectuons la transformation de chaque nombre en binaire.
La figure 15 montre le processus d'addition de ces deux nombres binaires.
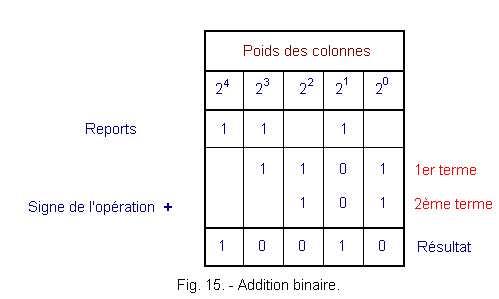
On obtient ainsi : 100102
→
1810
Les mêmes règles de signes s'appliquent aussi dans le cas des opérations binaires.
 5. 3. - LA SOUSTRACTION
DÉCIMALE OU DIFFÉRENCE
5. 3. - LA SOUSTRACTION
DÉCIMALE OU DIFFÉRENCE
Comme pour toute opération, il conviendra de procéder avec ordre.
On pose le premier terme, puis on
aligne en dessus le second terme, en faisant coïncider, dans les colonnes, les poids identiques.
On commence la soustraction par la
colonne la plus à droite (de poids le plus faible) en prenant comme résultat
le complément au chiffre soustrait, du chiffre soustracteur.
Le chiffre soustrait est celui qui
fait partie du nombre soustrait ; ce dernier correspond au premier terme.
Le chiffre soustracteur est celui
qui fait partie du nombre soustracteur ; ce dernier correspond au second terme.
Si le chiffre soustrait a une valeur
numérique inférieure à celle du chiffre soustracteur, il y a génération
d'un emprunt dans la colonne de poids immédiatement supérieur, que l'on
reporte sous forme de retenue dans cette même colonne, en retranchant cette retenue au chiffre soustrait.
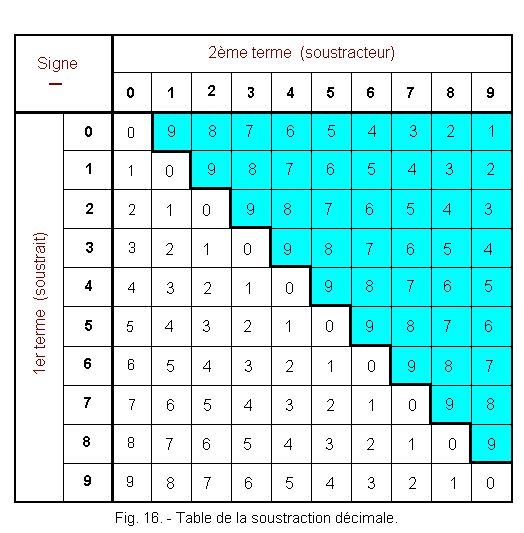
La figure 16 indique la table de
soustraction décimale. Dans la partie en cyan, le terme soustrait ayant une
valeur numérique inférieure à celle du terme soustracteur, l'opération génère
un emprunt dans la colonne de poids plus élevé. Le résultat de cette opération est une différence.
Exemple : Soit à soustraire
46
de 75.
La figure 17 montre le processus de cette soustraction en décimal.

En commençant par la colonne de poids le plus faible, on
constate, dans cet exemple, que l'on ne peut retrancher un nombre plus grand,
d'un nombre plus faible. On va devoir pratiquer un emprunt dans la colonne immédiatement supérieure.
Ainsi, nous pouvons réaliser la soustraction, le nombre
soustrait n'est plus 5, mais :
10
+ 5 soit 15, auquel nous pouvons
retrancher 6. La différence est
9.
Cet emprunt d'une unité dans la colonne des dizaines, il faut
à présent le retrancher dans cette même colonne, sans quoi le nombre
soustrait (75) verrait sa valeur numérique
modifiée (elle deviendrait égale à 85).
Une fois cette retenue effectuée, la soustraction peut
continuer jusqu'à la dernière colonne occupée.
Le résultat ou différence, est le complément du nombre
soustracteur par rapport au nombre soustrait.
Si on additionne le résultat et le nombre soustracteur, on
retrouve le nombre soustrait.
Dans le cas où le nombre soustrait a une valeur numérique plus
élevée ou égale au nombre soustracteur, l'opération est possible et le résultat
est positif ou nul.
Dans le cas où le nombre soustrait a une valeur numérique inférieure,
pour effectuer l'opération, on utilise un artifice. Il en existe plusieurs, le plus simple consiste à inverser les termes :
Quand on effectue cette inversion, on affecte à la valeur numérique
du résultat le signe négatif (-).
Ceci est une méthode rapide et pratique, car on peut utiliser
aussi l'emprunt dans la colonne immédiatement supérieure. Dans ce cas, on
obtient le complément à 100 du résultat.
On peut aussi procéder par addition du complément du nombre
soustracteur au nombre soustrait comme nous le verrons dans le chapitre consacré
aux opérations dans les machines numériques (le terme machine est utilisé ici
pour désigner un système travaillant avec des signaux numériques).
 5. 4. - LA SOUSTRACTION BINAIRE
5. 4. - LA SOUSTRACTION BINAIRE
Dune façon générale, les opérations décimales ou binaires
obéissent aux mêmes règles.
On retranche, dans la colonne de poids le plus faible, le
chiffre soustracteur du chiffre soustrait, autrement dit on prend le complément
du chiffre soustracteur par rapport au chiffre soustrait.
Si le chiffre soustrait a une valeur numérique plus faible que
celle du chiffre soustracteur, il y a emprunt au terme soustrait de la colonne de poids immédiatement supérieur.
On procède ainsi de colonne en colonne jusqu'à la dernière
représentant le poids le plus élevé.
De même que pour la soustraction décimale, si le terme
soustrait a une valeur numérique plus faible que le terme soustracteur, on inverse les opérateurs et on affecte au résultat le signe (-).
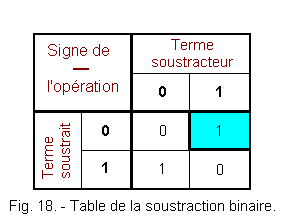
La figure 18 représente la table de soustraction binaire, la
case en cyan correspond à un emprunt au terme soustrait de la colonne de poids immédiatement supérieur.
Là encore, on constate une grande simplicité dans cette table
par rapport à celle de la soustraction décimale.
Exemple : Soit à soustraire
510
de 1110.
Effectuons la transformation en binaire :
10112
510
→
1012
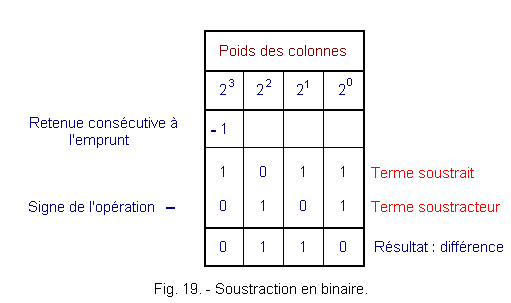
La figure 19 montre le déroulement de la soustraction binaire.
→
610
L'emprunt généré par l'opération de la colonne 22
est reporté sous forme de retenue au nombre de la colonne de poids immédiatement
supérieure (soit 23).
Les mêmes remarques que pour la soustraction décimale peuvent
s'appliquer aussi dans ce cas.
 5. 5. - LE PRODUIT OU MULTIPLICATION
DÉCIMALE
5. 5. - LE PRODUIT OU MULTIPLICATION
DÉCIMALE
La multiplication est une suite d'additions. Par exemple, si on
veut multiplier 15 x 5, il suffit
d'additionner cinq fois
le nombre 15 avec lui-même pour obtenir le résultat.
Les tables de multiplication sont faites pour nous éviter ces suites d'additions.
Le nombre qui représente la quantité que l'on doit multiplier
se nomme le multiplicande.
Le second terme du produit se nomme le multiplicateur.
Ainsi, dans l'exemple précédent, 15
est le multiplicande et 5 le multiplicateur.
La figure 20 représente la table de multiplication.
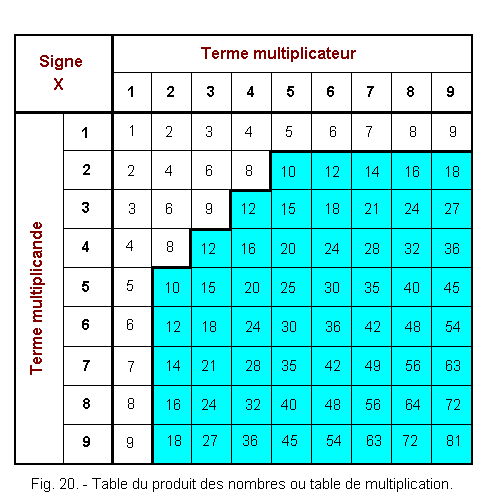
La lecture du résultat s'effectue dans la case correspondant à
l'intersection de la ligne du multiplicande avec la colonne du multiplicateur.
La partie en cyan génère un report qui devra être ajouté au
produit suivant.
Pour effectuer cette opération, on calcule le produit du
chiffre occupant le rang le moins élevé du multiplicateur avec chacun des
chiffres affectés aux différents poids du multiplicande, en commençant par le poids le plus faible.
Lorsque l'un de ces produits génère un report, celui-ci sera
additionné au produit suivant.
Quand ces produits sont effectués, ils constituent le premier résultat partiel.
Le second résultat partiel s'obtient en faisant le produit du
second chiffre du multiplicateur avec chacun des chiffres du multiplicande comme précédemment.
Ce second résultat partiel sera positionné sous le premier et
en le décalant d'un rang vers les poids plus élevés, car il s'agit d'un
produit obtenu avec le chiffre du multiplicateur occupant le rang de poids 101.
S'il y en a, les autres résultats partiels seront disposés
sous les précédents, en respectant le décalage dû au rang du chiffre
multiplicateur.
Le résultat final sera exprimé en faisant la somme des résultats partiels.
Il faut noter qu'il y a autant de résultats partiels qu'il y a de chiffres au multiplicateur.
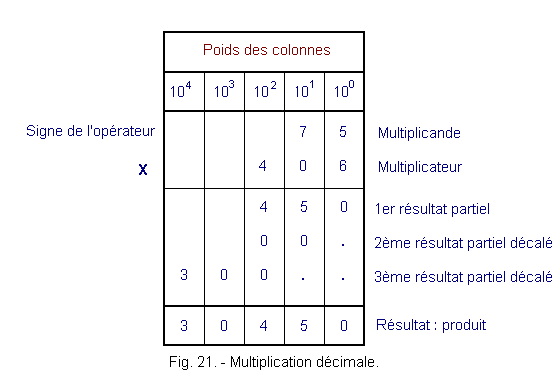
Exemple : Soit à multiplier
75 par 406.
La figure 21 décrit cette multiplication.
-
Le produit de 0 par un
nombre N est égal à
0.
-
Le produit d'un nombre N
par 0 n'a pas de sens, mais si l'on
applique la commutativité, on se replace dans le cas précédent et le résultat
est égal à 0.
Le signe du produit est déterminé d'après les règles énoncées
au début de ce chapitre, car le produit s'applique aux nombres relatifs (non seulement aux nombres positifs comme dans notre exemple). Nous rappelons
ci-dessous ces règles qui s'appliquent aussi aux opérations binaires :
-
un nombre positif multiplié par un nombre positif donne un
produit positif.
-
un nombre négatif multiplié par un nombre négatif donne
un produit positif
-
un nombre négatif multiplié par un nombre positif donne un
produit négatif (l'inverse donne le même résultat quand au signe).
 5. 6. - LE PRODUIT
BINAIRE
(retour)
5. 6. - LE PRODUIT
BINAIRE
(retour)
Du système binaire, basé sur deux éléments, découle une
simplification du calcul. Cette simplification est encore plus sensible avec la multiplication. En effet, cette opération ne génère aucun report ni emprunt.
La figure 22 représente la table de multiplication binaire.
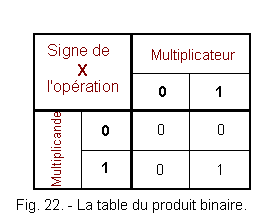
Comme pour le système à base 10,
la multiplication par 0 entraîne un résultat égal à 0. La multiplication par 1
entraîne la recopie du multiplicande.
La procédure d'obtention du résultat est identique à celle de
la multiplication décimale (ou pour tout autre multiplication dans un autre système de numération).
Exemple : Soit à multiplier
1110
par 2010.
Transformons ses deux nombres en binaire.
10112
2010
→ 101002
La figure 23 représente cette multiplication binaire.

Le résultat de ce produit est donc 110111002,
ce qui est équivalent au nombre décimal 22010.
 5. 7. - LA DIVISION OU QUOTIENT DÉCIMAL
5. 7. - LA DIVISION OU QUOTIENT DÉCIMAL
Le quotient, qui est l'opération inverse du produit, est par
conséquent, une suite de différences ou soustractions (le produit étant une suite d'addition).
Les règles de signes énoncées au début du chapitre
s'appliquent au quotient décimal ou binaire.
Le quotient est composé d'un nombre à diviser, que l'on nomme
le dividende, d'un nombre diviseur, que l'on
nomme diviseur.
Le nombre de fois que l'on peut soustraire le diviseur du
dividende, jusqu'à ce que cela ne soit plus possible, nous donne le quotient.
Si la dernière soustraction indique un résultat nul, le quotient est dit entier (ou exact).
Si au contraire, il y a un reste, le quotient est dit approché.
Exemple : Soit à diviser 75
par 15.
La figure 24 expose une méthode possible.

Nous pouvons soustraire cinq fois le nombre 15
du nombre 75, par suite, le quotient est 5 et puisque le dernier résultat est nul, le quotient est entier.
La multiplication du quotient par le diviseur, ajouté au reste s'il existe, redonne le dividende.
La procédure d'obtention du résultat, dans la pratique, ne
s'effectue pas selon cette méthode de soustractions successives qui est trop longue. De ce fait, cette opération est un peu plus délicate que les autres.
On commence par chercher combien de fois le diviseur est contenu
entièrement dans le nombre constitué par le ou les chiffres occupant les
rangs de poids les plus élevés du dividende.
Ce nombre constitue le premier dividende partiel. Le nombre de
fois que le diviseur est contenu dans ce premier diviseur partiel, constitue le
premier chiffre affecté au poids le plus élevé
du quotient.
On soustrait ensuite le produit du diviseur par ce quotient
partiel, du premier dividende partiel et cette différence (plus grande ou égale
à zéro) constitue, avec le chiffre occupant le poids suivant du dividende, le second dividende partiel.
On cherche, à nouveau, combien de fois le diviseur est contenu
dans ce second dividende partiel et le produit du diviseur par le second quotient lui est soustrait.
On effectue ces opérations jusqu'à ce que le dividende ne possède
plus de chiffre significatif, si la dernière différence est égale à zéro,
le quotient est dit exact, (le dividende est un multiple entier du diviseur).
S'il n'en est pas ainsi, le quotient est dit
approché
et la division comporte un reste.
Exemple : Soit à diviser 405 par 3.
Pour plus de facilité, on peut disposer l'opération de la façon
suivante :

La figure 25 donne la procédure adoptée pour effectuer cette division.
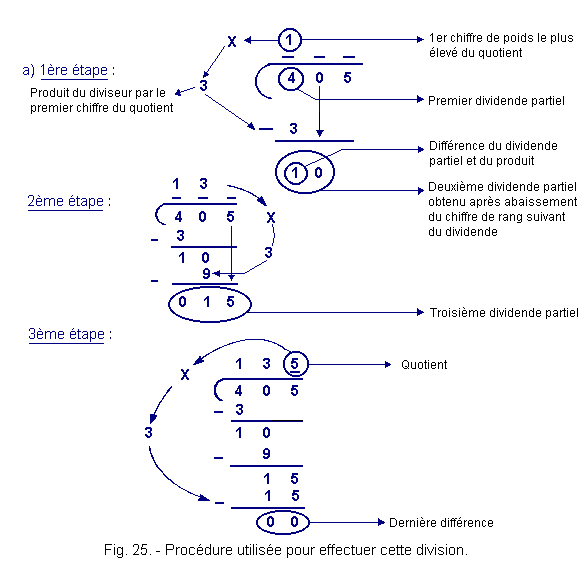
Nous sommes en présence d'un quotient exact (135),
la dernière différence étant égale à zéro. Le nombre 405 est un multiple de 3.
Cette procédure implique deux opérations :
-
la multiplication
-
la soustraction.
Ces opérations sont décrites aux chapitres 5.5 et 5.3 ainsi que les tables correspondantes.
Ces opérations sont plus faciles à effectuer qu'à énumérer,
car nous avons acquis des automatismes.
Il n'est pas question de remettre en cause ces automatismes,
mais ils font parfois oublier les processus élémentaires que nous utilisons pour des tâches fréquentes.
En les rappelant, la similitude entre les opérations décimales
et binaires apparaît mieux et les procédures utilisées dans les machines numériques
vous paraîtront plus familières.
 5. 8. - LE QUOTIENT BINAIRE
5. 8. - LE QUOTIENT BINAIRE
Le cheminement en vue de l'obtention du résultat est identique
à celui de la division décimale. Par conséquent, nous allons passer à un exemple.
La procédure pratique implique deux opérations :
Ces opérations nous sont familières, leurs
tables sont représentées dans les figures 22 et
18.
Soit à diviser 101012 (2110)
par 112 (310).
La figure 26 représente la procédure utilisée qui est tout à
fait analogue à la méthode employée en décimal.
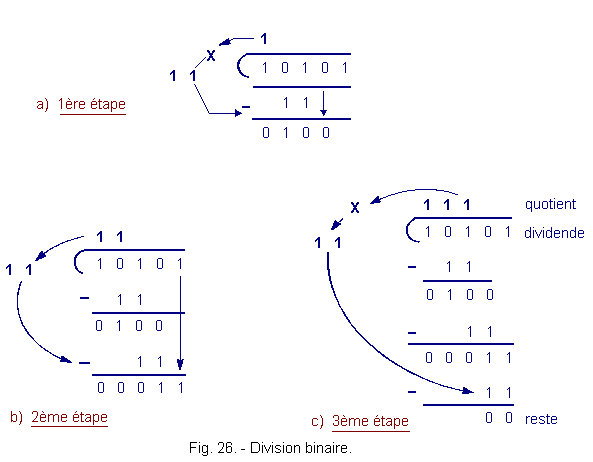
La division s'arrête là, car le reste est
égal à zéro et il n'y a plus de chiffre, au dividende, à combiner avec le reste.
Le résultat de la division est donc 1112
soit 710.



 Complément d'un nombre
Complément d'un nombre


.gif)
 pour l'union et
pour l'union et  pour l'intersection).
pour l'intersection).

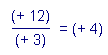

.gif)














 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet.
Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Page suivante
Page suivante