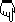 Semi-conducteurs intrinsèques Semi-conducteurs intrinsèques |
 Bas de page Bas de page |
Structures des Cristaux - Semi-Conducteurs Intrinsèques :
2. - STRUCTURES DES CRISTAUX
Le fonctionnement des transistors dépend des propriétés de la couche externe des atomes de certains corps, dits corps semi-conducteurs, mais il est basé sur l'état d'agrégation de ces corps.
Les caractéristiques physiques fondamentales des semi-conducteurs se manifestent exclusivement lorsque le matériau est à l'état solide.
Il faut en plus que ce matériau se trouve dans un état solide particulier dit état cristallin. C'est pour cette raison que les transistors ou les diodes à semi-conducteurs sont appelés des dispositifs à cristal.
L'état cristallin se distingue des autres états solides par le fait que les atomes occupent dans l'agrégat une position fixe selon un dessin géométrique répété, plus ou moins complexe.
Prenons par exemple un cristal très pur de chlorure de sodium (sel de cuisine).
Le chlorure de sodium est un composé constitué d'atomes de chlore et de sodium en parties égales. Si nous pouvions agrandir cinquante millions de fois un minuscule grain de chlorure de sodium, les atomes apparaîtraient comme sur la figure 5-a.
Cette disposition se répète, toujours égales à elle-même, à mesure qu'augmentent les dimensions du grain de cristal.
La structure réticulaire de la figure 5-a est fondamentale pour de nombreux types de cristaux. Il existe évidemment d'autres structures réticulaires cristallines de substances simples et composées.
On peut voir figure 5-b, la représentation du cristal de sélénium, substance simple employée dans la fabrication des redresseurs solides.
Les atomes, dans la structure cristalline de sélénium, sont disposés en spirales autour d'axes parallèles et celles-ci se regroupent en couches superposées.
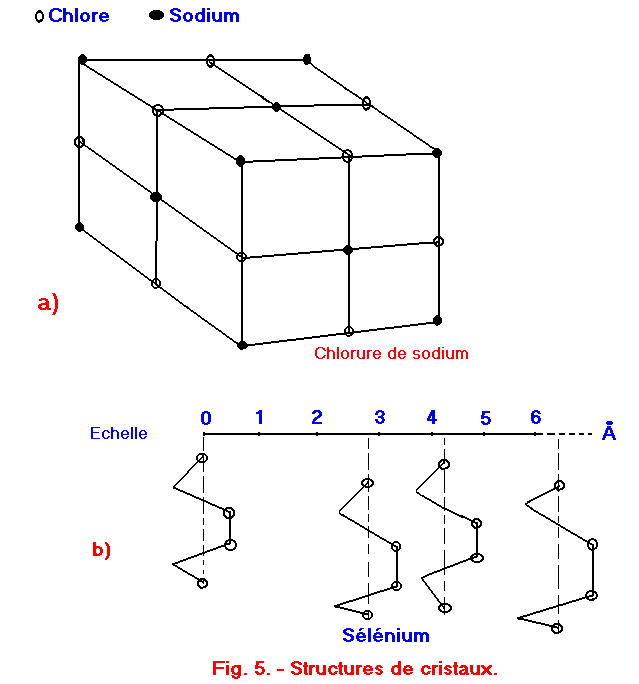
Parmi les structures cristallines, celle du diamant a une grande importance dans l'étude des semi-conducteurs.
Le diamant (figure 6-a) est constitué d'atomes de carbone, disposés de telle sorte que chaque atome se trouve entouré par quatre autres, tous à égale distance de l'atome central et uniformément dans l'espace environnant (figure 6-b).
La distance d, entre l'atome central et les quatre atomes voisins est constante en tous points du réseau (cette distance est d'environ 2 angströms).
Les atomes de cristal sont maintenus ensemble par des liens covalents, du même type que ceux de la figure 4-b.
En nous rappelant ce qui vient d'être dit sur la nature de ce lien, nous pouvons comprendre que tout l'espace entre les atomes est occupés par une intense circulation électronique. Les électrons se promènent en effet, dans les espaces vides du réseau cristallin, en passant d'une orbite à l'autre, mais ils ne sont jamais vraiment libres : ils restent toujours liés au réseau formé par les atomes auxquels ils appartiennent initialement. Ils ne pourraient pas, sous l'action d'un champ électrique extérieur, former un flux continuel de courant. En d'autres termes, cela signifie que le diamant est un mauvais conducteur d'électricité.
Pour représenter de façon plus simple la structure cristalline du diamant, on peut avoir recours à la représentation plane (figure 7).
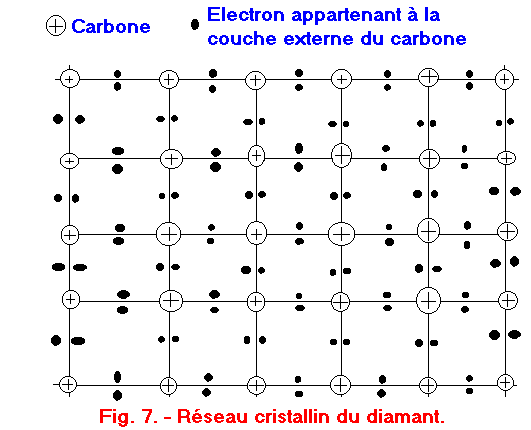
Cette figure met mieux en évidence le fait que les distances entre atomes sont égales et permet de mieux comprendre l'existence des liens covalents.
![]() 3. - SEMI-CONDUCTEURS INTRINSÈQUES
3. - SEMI-CONDUCTEURS INTRINSÈQUES
On appelle semi-conducteurs, les substances dont la conductivité électrique est intermédiaire entre celle des conducteurs et celle des isolants.
L'oxyde de cuivre et le sélénium, utilisés dans certains types de redresseurs, sont des semi-conducteurs, de même que divers autres oxydes et sels métalliques, mais ce sont le germanium et le silicium qui ont le plus d'importance. La figure 8 représente l'atome de chacun de ces deux éléments.
On peut remarquer que pour ces deux corps, la couche externe des atomes ne comprend que quatre électrons.
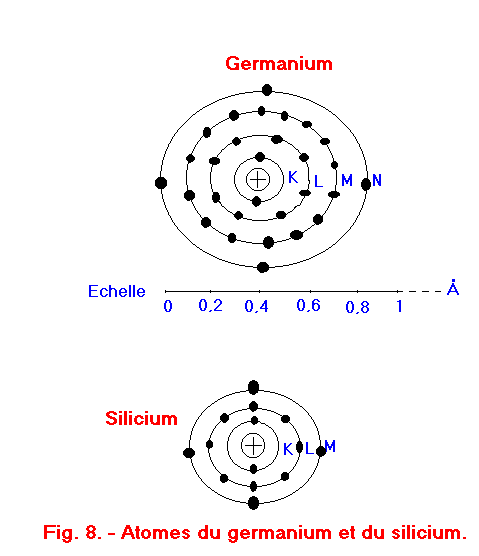
Ces éléments sont donc du type tétravalent, comme le carbone pur (diamant).
Remarquons aussi que le carbone, le silicium et le germanium, appartiennent au même groupe dans la classification de MENDELEYEV (groupe IV, figure 3). Ainsi, tout ce qui a été dit sur le réseau cristallin du carbone et sur les liens covalents de ce corps reste valable pour le germanium et le silicium.
Cependant, en examinant le réseau cristallin du diamant, on a signalé que les électrons appartenant à la couche externe de chaque atome, vont d'une orbite à l'autre mais qu'ils restent liés et ne peuvent pas participer à la formation d'un courant électrique. Or, pour certains cristaux, la circulation électronique peut être influencée plus ou moins par des causes extérieures (un champ électrique par exemple) et dans ce cas de nombreux électrons peuvent se réunir en un flux de courant.
Cela signifie que l'on peut avoir des cristaux plus ou moins bon conducteurs d'électricité ou des cristaux isolants, comme le diamant.
Les cristaux de germanium et de silicium sont dans la première catégorie et nous allons voir comment se produit la conduction électrique.
Pour clarifier les explications, subdivisons les électrons des couches externes en deux catégories :
-
Les électrons de valence, représentés figure 9 par des points noirs ;
-
Les électrons de conduction, représentés sur cette même figure par des points noirs traversés d'une flèche.
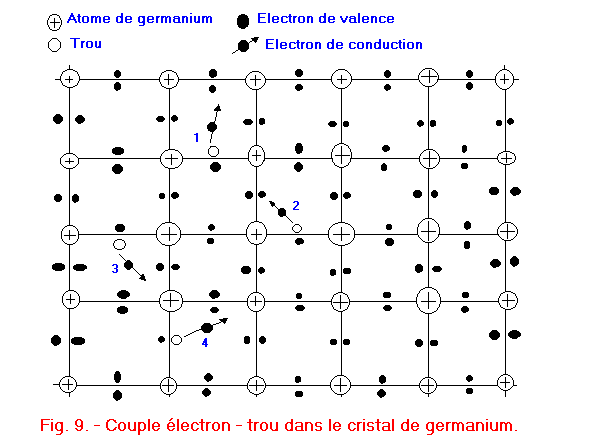
Les électrons de valence sont ceux, qui tout en se déplaçant d'un atome à l'autre, restent liés au réseau (comme dans le cas du diamant).
Les électrons de conduction sont ceux, qui pendant les divers déplacements, acquièrent assez d'énergie pour rompre les liens covalents.
Dans un cristal très pur, géométriquement parfait et maintenu à une température très proche du zéro absolu (- 273,16°C), tous les électrons des atomes appartiennent à la catégorie des électrons de valence ou pour utiliser une expression courante en physique, appartiennent à la bande de valence.
En élevant la température ou sous l'effet d'une déformation du réseau ou encore en plaçant le cristal dans un champ électrique intense, une partie des électrons de valence gagne une certaine énergie et peut se libérer du réseau, c'est-à-dire passer de la bande de valence à la bande de conduction. Ce phénomène peut être plus ou moins important selon le type de cristal.
A la température de 18°C, pour le diamant, ce phénomène est négligeable ; pour le germanium, un électron sur un milliard d'atomes passe de la bande de valence à la bande de conduction (un électron sur 4 milliards d'électrons de valence devient libre).
A première vue, en fonction des nombres donnés, on pourrait croire qu'un électron sur quatre milliards constitue une quantité négligeable. En réalité, il faut tenir compte du fait que dans un centimètre cube de germanium, il y a environ 1 x 1022 atomes, ce qui donne environ dix mille milliards d'électrons libres. Cette quantité n'est donc plus négligeable et suffit à rendre le cristal conducteur.
Mais que se passe-t-il dans un cristal où un électron est devenu libre ?
Cet électron se promène de façon désordonnée dans les espaces du réseau, contrairement aux électrons de valence qui parcourent les mêmes espaces sur des orbites bien définies. D'autre part, à partir du moment où le lien covalent est rompu et que l'électron laisse une place libre, il se créé un vide sur une orbite.
En un point du réseau, il existe donc un trou (on dit aussi cavité ou lacune).
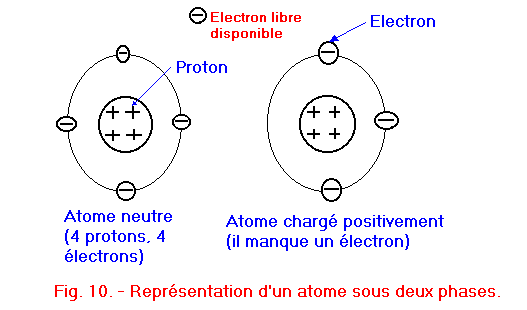
Ce phénomène est mis en évidence sur la figure 9 où l'on peut voir quatre électrons libres (électrons de conduction) et aussi quatre trous portant les numéros 1 - 2 - 3 et 4. Le trou représente une charge électrique égale à celle de l'électron mais de signe inverse. En effet, l'atome est neutre avec tous ses électrons. S'il en perd un, cet électron libre représente une charge négative disponible ; mais l'atome n'est plus neutre puisqu'il a perdu un électron ; il acquiert donc une charge positive, charge provenant des protons dont l'influence n'est plus compensée par le même nombre d'électrons qu'à l'origine. (La figure 10 permet de mieux comprendre cette explication.
Ainsi, lorsque dans le cristal très pur il y a de nombreux électrons libres, il existe autant de trous. Il ne faut pas cependant croire que ces trous occupent une position immuable. En effet, dès qu'un trou vient d'être créé par fuite d'un électron, il est presque instantanément occupé par un électron de valence. Ce trou disparaît donc, mais ne reforme ailleurs dans la place laissée libre par l'électron de valence en question et ainsi de suite.
Nous pouvons donc retenir que les trous se déplacent d'un point à un autre du réseau, de façon imprévisible et désordonnée comme les électrons libres.
Le mouvement désordonné des électrons de conduction et des trous constituent l'aspect fondamental de la conductibilité électrique dans les semi-conducteurs.
Les figures 11 et 12 permettent de bien illustrer les phénomènes décrits précédemment.
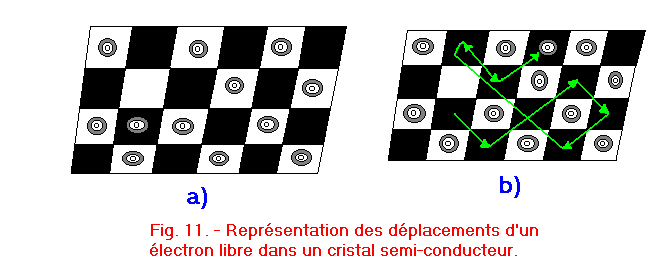
L'échiquier de la figure 11-a représente le réseau d'un cristal semi-conducteur. Les pions se trouvant dans les cases blanches correspondent aux électrons de valence et le pion de la case noire à l'électron de conduction.
La case blanche vide représente le trou créé par l'électron libre lors de son passage de la bande de valence à la bande de conduction.
L'électron peut se déplacer de façon libre et désordonnée dans les espaces du réseau, tout comme le pion se trouvant dans la case noire peut être déplacé sur l'échiquier (figure 11-b). Dans le même temps, le trou se déplace de façon désordonnée ; son parcours n'est pas aussi simple que celui de l'électron libre. En effet, pour qu'un trou puisse changer de position, il faut qu'un électron de valence vienne l'occuper, laissant ainsi un nouveau trou libre ; exactement comme pour déplacer la case blanche libre de la figure 12-a, il faut qu'elle soit occupée par le pion d'une autre case blanche.
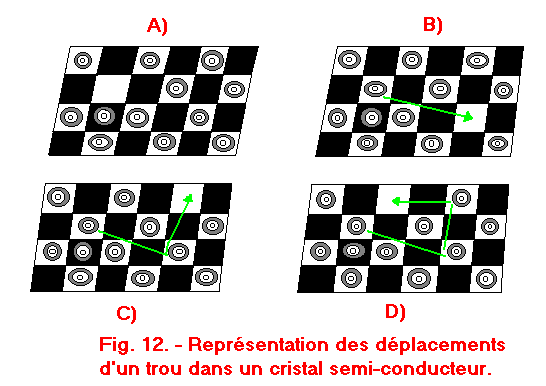
En répétant ce jeu avec d'autres pions (figures 12-b, 12-c et 12-d), la case blanche libre semble se promener de façon incohérente à travers l'échiquier, tout comme les trous dans le réseau du cristal.
En général, le mouvement d'un électron libre et celui d'un trou n'ont pas une durée limitée. En effet, en raison de l'agitation thermique de toutes les particules du cristal, l'électron libre à un moment donné, heurte un autre électron et perd ainsi son énergie. De ce fait, il est attiré par un trou qui cesse ainsi d'exister.
La figure 13 illustre le parcours effectué par un électron libre et par un trou.
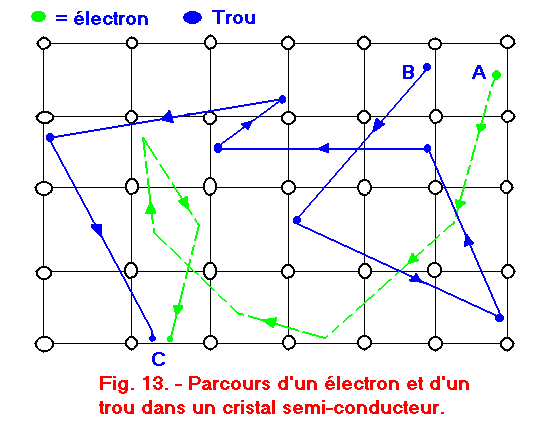
L'électron part de A et suit par exemple le chemin représenté en pointillés de couleur vert pour arriver au point C. En principe, il se déplace le long de trajectoires rectilignes en changeant de direction toutes les fois qu'il heurte d'autres particules. Quant au trou, partant du point B et suivant la ligne en trait continu, il arrive lui aussi au point C où il disparaît, l'électron ayant perdu toute son énergie à la suite des chocs subis avec les particules.
Nous venons de voir jusqu'à présent les cristaux semi-conducteurs très pur et géométriquement parfaits dans lesquels le nombre des électrons libres est exactement égal au nombre de trous. Ces semi-conducteurs s'appellent des semi-conducteurs intrinsèques.
Pour utiliser ceux-ci afin de réaliser des transistors, il faut modifier leur structure par un traitement approprié, c'est ce que nous verrons dans la prochaine leçon semi-conducteurs 2.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente
|
 Page suivante Page suivante
|
Nombre de pages vues, à partir de cette date : le 23 MAI 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 5. 14 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 22 MAI 2023.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en MAI 2023.

