Fonction NOR Fonction NOR
|
 Fonction OU EXCLUSIF Fonction OU EXCLUSIF
|
 Vérification du fonctionnement d'un OU EXCLUSIF Vérification du fonctionnement d'un OU EXCLUSIF
|
 Fonction NOR EXCLUSIF Fonction NOR EXCLUSIF
|
 Fonction identité logique Fonction identité logique |
 Bas de page Bas de page
|
Fonction NAND - Fonction NOR - Fonction OU Exlusif - Fonction NOR Exclusif :
Dans cette leçon, nous allons terminer l'examen des fonctions logiques de base telles que les fonctions NAND, NOR, OU EXCLUSIF... et résoudre quelques problèmes à l'aide des théorèmes de DE MORGAN et de la méthode de QUINE MAC CLUSKEY.
1. - FONCTIONS DÉRIVÉES DES FONCTIONS FONDAMENTALES
1. 1. - FONCTION NAND (NON - ET)
Le circuit NAND bien que dérivé du circuit ET (AND) est plus utilisé et plus courant que celui-ci. En effet à l'origine, il était technologique-ment plus facile à réaliser et moins coûteux, ce qui explique qu'il a été le circuit le plus fréquemment utilisé. Toutefois, ceci n'est plus tout à fait vrai car les progrès technologies ont vu les prix et les performances de l'ensemble des circuits évoluer très rapidement.
1. 1. 1. - LE CIRCUIT NAND
Son symbole est celui de la figure 1.
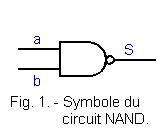
Un circuit NAND est obtenu en mettant en série une porte ET et un inverseur comme représenté figure 2.
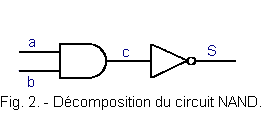
Étudions la relation existant entre a, b et S ; pour cela partons d'un circuit ET suivi d'un circuit inverseur.
On obtient la table de vérité du
circuit NAND en écrivant d'abord l'équation
c = a . b puis S = ![]() .
.
La table de vérité du circuit ET est représentée figure 3 :
.gif)
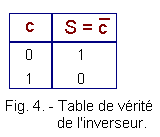
La table de vérité du circuit inverseur est reproduite figure 4 :
On peut facilement en déduire la table de vérité du circuit NAND qui est représentée figure 5 :
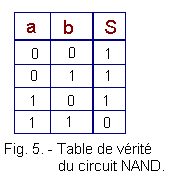
La sortie d'un circuit NAND n'est à l'état logique 0 que lorsque les deux entrées sont à l'état 1. Il suffit qu'une seule des entrées soit à 1 pour que la sortie devienne 1.
La fonction logique NAND
peut être résumée par l'équation booléenne ![]() suivant le nombre des entrées.
suivant le nombre des entrées.
On retrouve le signe . symbolisant le produit ET et la barre indiquant la complémentation.
1. 1. 2. - REPRÉSENTATION D'EULER (figure 6)
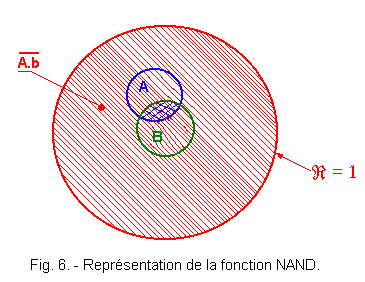
La fonction ET
telle que S = a . b est l'intersection de
A
et B (surface hachurée bleue) alors que
l'inverse de a . b
soit ![]() est l'ensemble des surfaces hachurées rouge.
est l'ensemble des surfaces hachurées rouge.
1. 1. 3. - CIRCUIT ÉLECTRIQUE (Retour à la théorie N°3 TS)
La figure 7 représente le circuit électrique utilisé pour réaliser une fonction NAND à deux variables d'entrées a et b, S étant la sortie.
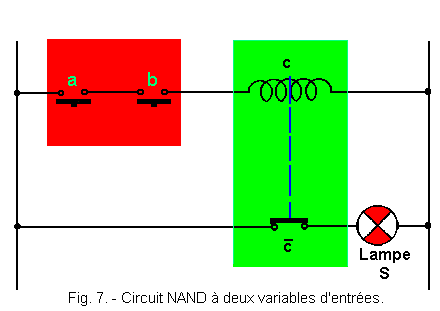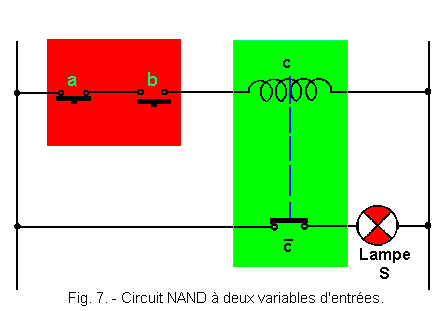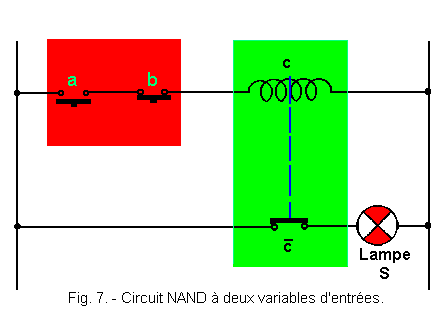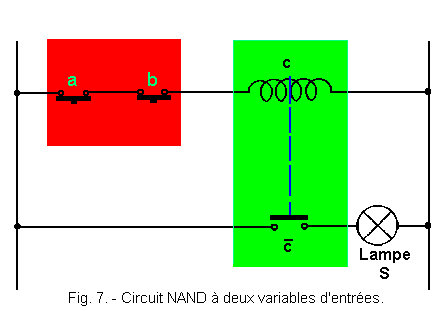
Les contacts utilisés a et b sont des contacts travail, c'est-à-dire ouverts au repos. Si nous nous reportons à la théorie 2, nous voyons que l'ensemble représenté en rouge est un ET réalisé avec des contacts de telle sorte que a . b = C.
Or, C à l'intérieur de l'ensemble tramé en vert, est un relais dont la bobine est matérialisée
par le signe ![]() .
Il commande le contact
.
Il commande le contact ![]() qui est un contact repos de telle sorte que l'on peut écrire le tableau de
fonctionnement représenté figure 8.
qui est un contact repos de telle sorte que l'on peut écrire le tableau de
fonctionnement représenté figure 8.

Avec la convention logique positive, on peut écrire :
Contact fermé = 1 ; contact ouvert = 0
Lampe allumée = 1 ; lampe éteinte = 0
Relais alimenté = 1 ; relais non alimenté = 0
D'où la table de vérité représentée figure 9 :

Nous voyons dans cette table de vérité que la sortie est toujours à 1 sauf pour les deux entrées à 1 ou S = 0.
![]() 1. 2. - FONCTION NOR
(Retour à la théorie N° 3 TS)
1. 2. - FONCTION NOR
(Retour à la théorie N° 3 TS)
Comme pour la porte ET qui devient après adjonction d'un inverseur une porte NAND, avec un circuit OU suivi d'un inverseur à sa sortie on obtient un circuit NOR dont le symbole graphique est celui de la figure 10-a :
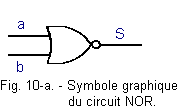
Le circuit NOR équivaut à un circuit OU suivi d'un inverseur comme représenté figure 10-b :
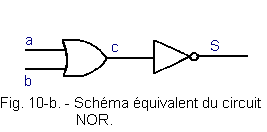
Étudions la relation existante entre a, b et S, pour cela partons d'un circuit OU suivi d'un circuit inverseur.
On obtient la table de vérité du
circuit NOR en écrivant d'abord l'équation
C = a + b puis
S = ![]() .
.
La table de vérité du circuit OU est représentée figure 11 :
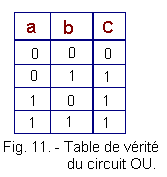
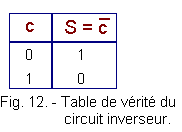
La table de vérité du circuit inverseur est représentée figure 12 :
La table de vérité du circuit NOR peut alors être facilement déduite (figure 13) :
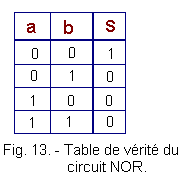
La sortie d'un circuit NOR n'est à l'état logique 1 que lorsque les deux entrées sont à 0.
La fonction logique
NOR
peut être résumée par l'équation booléenne ![]() suivant le nombre des entrées.
suivant le nombre des entrées.
On retrouve le signe + symbolisant la somme logique OU et la barre indiquant la complémentation.
1. 2. 1. - REPRÉSENTATION D'EULER (figure 14)

La fonction OU
tel que S = a + b est l'union de
A et B (surface hachurée bleue) alors que
l'inverse de a + b soit ![]() est l'ensemble des surfaces hachurées rouge.
est l'ensemble des surfaces hachurées rouge.
1. 2. 2. - CIRCUIT ÉLECTRIQUE
La figure 15 représente le circuit électrique utilisé pour réaliser une fonction NOR.
Les contacts utilisés a et b sont des contacts travail, c'est-à-dire ouverts au repos. Si nous nous reportons à la théorie 2, nous voyons que l'ensemble représenté en rouge est un OU réalisé avec des contacts de telle sorte que a + b = C.
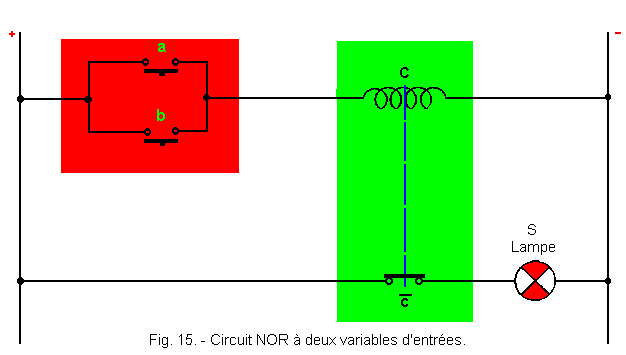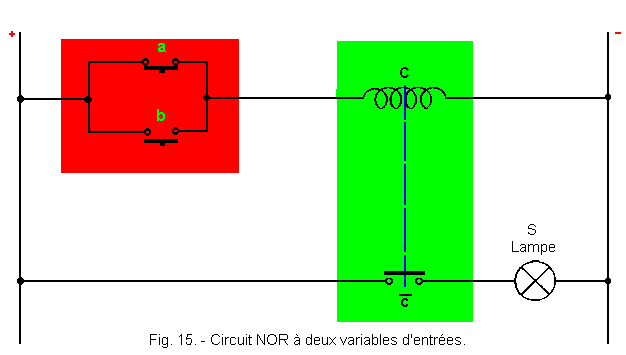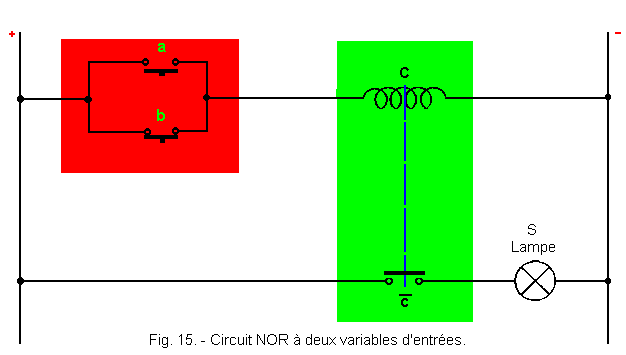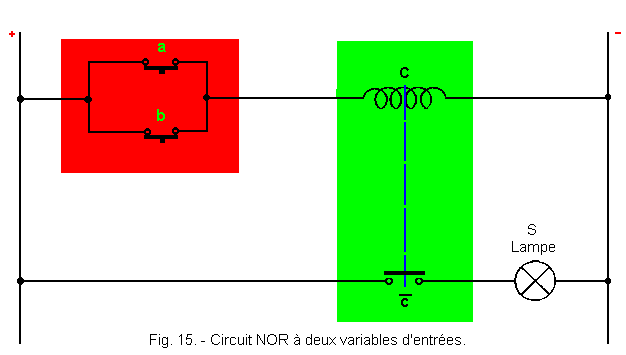
Or, C
à l'intérieur de l'ensemble hachuré vert est un relais dont la bobine est matérialisée
par le signe ![]() .
Il commande le contact
.
Il commande le contact ![]() qui est un contact repos de telle sorte que l'on peut écrire le tableau de
fonctionnement suivant (figure 16) :
qui est un contact repos de telle sorte que l'on peut écrire le tableau de
fonctionnement suivant (figure 16) :
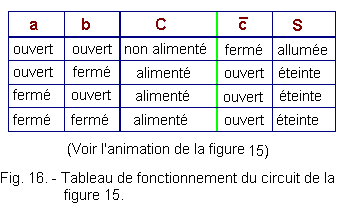
Compte tenu de la convention logique positive, on peut déduire la table de vérité de la figure 17 :
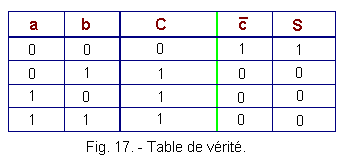
Nous voyons dans cette table de vérité que la sortie est toujours à 0 sauf pour les deux entrées à 0 ou S = 1.
![]() 1. 3. - FONCTION OU
EXCLUSIF (EXCLUSIVE OR)
1. 3. - FONCTION OU
EXCLUSIF (EXCLUSIVE OR)
1. 3. 1. - TABLE DE VÉRITÉ
La fonction OU exclusif est plus complexe que l'ensemble des fonctions que nous venons d'analyser.
Rappelons-nous la table de vérité de la fonction OU inclusif (figure 18) :
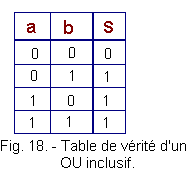
Nous voyons que la sortie S de l'opérateur OU était à 1 lorsque a OU b ou les deux étaient à 1.
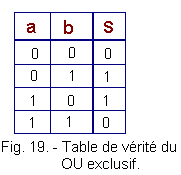
Dans le cas du OU exclusif, il n'en sera pas de même. En effet, pour S = 1, il faudra que a OU b soit à 1 exclusivement, c'est-à-dire que S ne sera pas à 1 lorsque a et b sont simultanément à 1. Le OU exclusif comme son nom l'indique exclut cette possibilité.
La figure 19 montre la table de vérité du OU exclusif :
On écrit alors que S
= a ![]() b que l'on énonce S égal a OU exclusif b.
b que l'on énonce S égal a OU exclusif b.
Le signe ![]() est le symbole du OU exclusif dans les équations logiques.
est le symbole du OU exclusif dans les équations logiques.
Dans les schémas, on utilise le symbole graphique représenté figure 20.
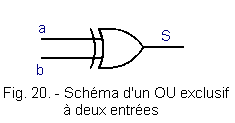
1. 3. 2. - REPRÉSENTATION D'EULER (Figure 21)
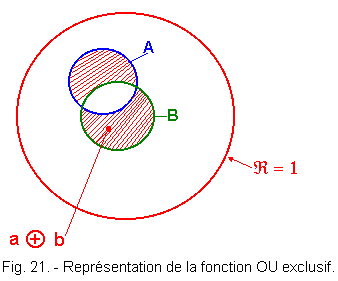
La fonction OU
exclusif telle que S = a
![]() b est la surface hachurée telle que S = 1
pour a = 1 ou
b = 1,
c'est-à-dire la réunion des ensembles A et B à l'exclusion de la surface commune à
A et B.
b est la surface hachurée telle que S = 1
pour a = 1 ou
b = 1,
c'est-à-dire la réunion des ensembles A et B à l'exclusion de la surface commune à
A et B.
1. 3. 3. - SCHÉMA RÉALISÉ AVEC DES OPÉRATEURS LOGIQUES SIMPLES
Comme nous l'avons dit au début de ce chapitre, la fonction OU exclusif est plus complexe que les fonctions NAND ou NOR.
Essayons par le raisonnement
graphique de trouver une équation de S
telle que le signe ![]() disparaisse pour ramener la fonction OU exclusif
à des fonctions ET et
OU
classiques ou des fonctions inversions.
disparaisse pour ramener la fonction OU exclusif
à des fonctions ET et
OU
classiques ou des fonctions inversions.
Nous voyons que S est formée de deux surfaces distinctes :
-
- La surface S1 incluse à l'intérieur de A
-
- La surface S2 incluse à l'intérieur de B.
Représentons figure 22 la surface S1.

L'ensemble ![]() hachuré en rouge est le complément de B par rapport à Â.
hachuré en rouge est le complément de B par rapport à Â.
Nous voyons que la surface S1,
représentée par l'ensemble hachuré verticalement en noir, est l'intersection
de ![]() et de A.
et de A.
Nous pouvons donc écrire S1 = a![]() car si A et B sont les ensembles pour lesquels a et
b sont respectivement à 1, S1 sera l'ensemble pour lequel a = 1 et b = 0.
car si A et B sont les ensembles pour lesquels a et
b sont respectivement à 1, S1 sera l'ensemble pour lequel a = 1 et b = 0.
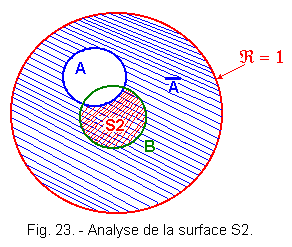
Nous pouvons facilement en suivant
le même raisonnement voir sur la figure 23 que S2 = ![]() b
puisque S2 est l'intersection de
b
puisque S2 est l'intersection de ![]() et de B.
et de B.
A partir de la table de vérité de la fonction OU exclusif (figure 19), nous pouvons établir le tableau de karnaugh de cette fonction représenté figure 24.
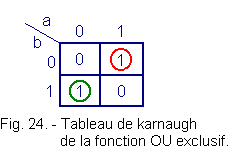
A cet égard, il est absolument fondamental de se rappeler comment on réalise un tableau de karnaugh à partir de la table de vérité.
Les valeurs de la sortie S pour une combinaison de a et de b donnée sont reportées dans la case se trouvant à l'intersection des valeurs de a et b considérées, portées sur les côtés de la table. Nous vous conseillons de revenir éventuellement à la théorie 2 afin de revoir si nécessaire les tableaux de karnaugh.
On en déduit :
-
groupement rouge S = a
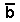 ,
, -
groupement vert S =
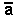 b,
b,
D'où l'on peut écrire :
S = ![]() b
+ a
b
+ a![]()
Ceci confirme le résultat obtenu par la décomposition graphique réalisée grâce à la représentation d'Euler.
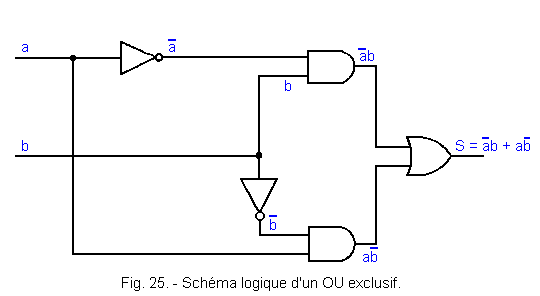
Nous pouvons donc maintenant construire le schéma de la figure 25 qui représente une fonction OU exclusif réalisée à partir de fonctions ET, OU et NON.
![]() 1. 3. 4. - VÉRIFICATION
DU FONCTIONNEMENT A PARTIR DU SCHÉMA LOGIQUE ET RECONSTITUTION
DE LA TABLE DE VÉRITÉ
1. 3. 4. - VÉRIFICATION
DU FONCTIONNEMENT A PARTIR DU SCHÉMA LOGIQUE ET RECONSTITUTION
DE LA TABLE DE VÉRITÉ
Sur les figures 26 a, b, c et d sont reportées les quatre combinaisons pouvant être prises par deux entrées a et b.
Sur chacune de ces figures sont reportées les différents niveaux logiques en entrée et en sortie de chaque porte.
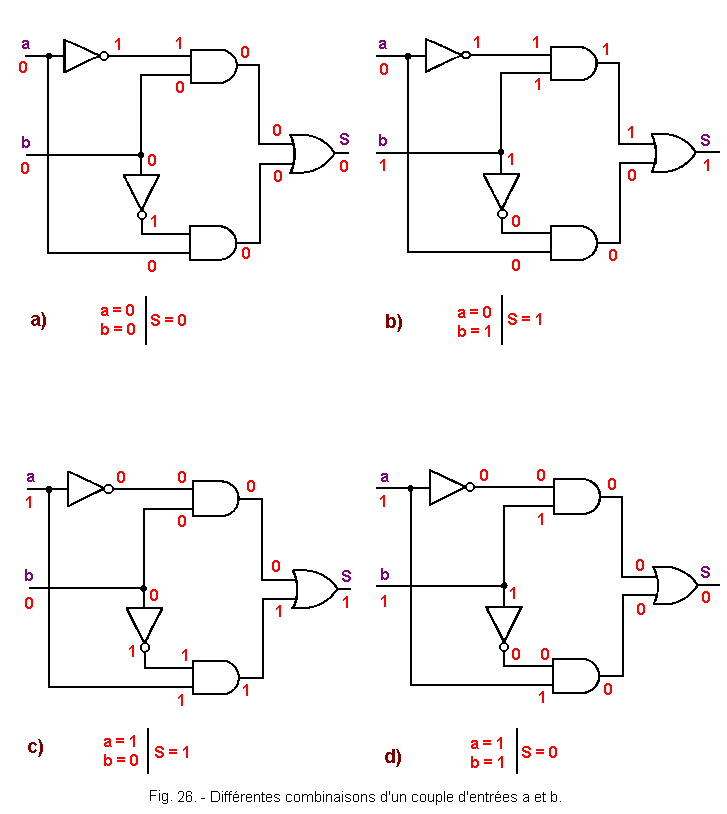
Nous pouvons récapituler les quatre cas de la figure 26 dans le tableau de Karnaugh de la figure 27. Le tableau obtenu correspond bien en tous points au tableau de la fonction OU exclusif.
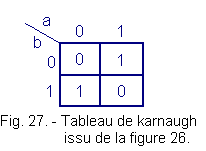
Ce dernier exercice a pu vous paraître inutile, en réalité il n'en est rien car il est nécessaire de se sentir parfaitement à l'aise dans les tableaux de Karnaugh, les tables de vérités et les schémas afin de pouvoir faire la transformation dans un sens ou dans l'autre sans erreur et éventuellement lors de l'élaboration d'un circuit complexe de se vérifier en utilisant chaque fois une méthode différente.
![]() 1. 4. - FONCTION NOR
EXCLUSIF (EXCLUSIVE NOR)
1. 4. - FONCTION NOR
EXCLUSIF (EXCLUSIVE NOR)
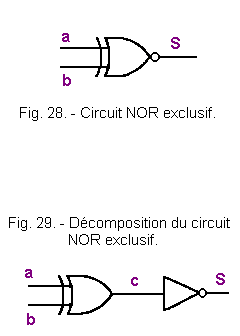
Le circuit NOR exclusif dont le symbole est représenté figure 28 s'obtient d'une manière identique aux NAND et aux NOR mais en utilisant un circuit OU exclusif suivi d'un inverseur (figure 29).
L'équation logique du
NOR exclusif à deux entrées est ![]() .
Cette équation indique bien que le NOR exclusif
réalise
l'opération OU exclusif et complémente le
résultat (barre au-dessus).
.
Cette équation indique bien que le NOR exclusif
réalise
l'opération OU exclusif et complémente le
résultat (barre au-dessus).
Vous pouvez utiliser vous-même le processus suivi pour les portes NAND et NOR afin de retrouver la table de vérité. Nous nous bornerons à indiquer cette table, figure 30, pour un NOR exclusif à deux entrées.
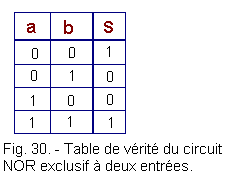
Un circuit NOR exclusif, comme un circuit OU exclusif, sert à détecter la présence d'un signal unique soit a, soit b (on dit que le signal a ou b est présent lorsqu'il a un niveau logique 1).
Dans le cas du circuit NOR exclusif, on peut également vérifier l'égalité entre deux signaux a et b. En effet, S est à 1 pour a et b simultanément à 1, mais aussi pour a et b simultanément à 0.
![]() 1. 5. - FONCTION IDENTITÉ LOGIQUE
1. 5. - FONCTION IDENTITÉ LOGIQUE
La fonction identité logique n'existe pas en tant que telle sous forme de circuits intégrés. Toutefois, elle peut rendre des services dans certains automatisme pour créer des sécurités.
Supposons, par exemple, que d'une part une variable a indique le sens de rotation d'un moteur (a = 1 "marche avant", a = 0 "marche arrière") et, que d'autre part pour des raisons de sécurité on doit vérifier qu'un outil est bien positionné sur la machine suivant le sens de rotation choisi (b = 1 "taille avant", b = 0 "taille arrière").
On voit immédiatement que par raison de sécurité, il faut que la mise en route soit autorisée uniquement pour a = b = 1 OU pour a = b = 0. La matérialisation de l'autorisation de mise en route sera réalisée par exemple au moyen d'une lampe.
L'équation d'une telle identité logique est :
S = ab + ![]()
![]()
Que l'on écrit :
S = a ![]() b
b
La figure 31 donne le schéma électrique de cette identité logique réalisée avec des contacts.
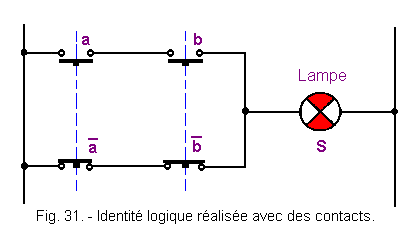
Vous savez maintenant qu'un ET se matérialise par des contacts en série et un OU par des contacts en parallèle.
La rangée de contacts travail a,
b matérialise donc ab alors que la rangée de contacts repos matérialise
![]()
![]() .
Les deux rangées de contacts étant en parallèle, on a donc :
.
Les deux rangées de contacts étant en parallèle, on a donc :
S = ab + ![]()
![]()
La figure 32 donne le schéma électrique de la même identité logique mais réalisée cette fois-ci à l'aide de portes électroniques.
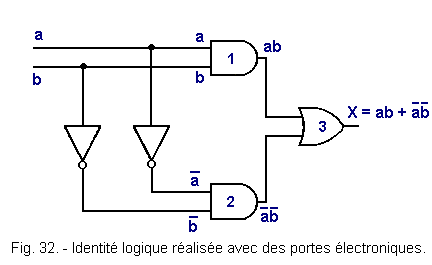
La réalisation d'un tel schéma est
encore plus simple, on établit ab et ![]()
![]() au moyen de deux portes ET
(respectivement portes n° 1 et n° 2),
au moyen de deux portes ET
(respectivement portes n° 1 et n° 2), ![]() et
et ![]() étant obtenus auparavant par deux inverseurs.
étant obtenus auparavant par deux inverseurs.
Le circuit OU (porte n° 3) réalise quant à lui l'opération finale pour obtenir :
S = ab + ![]()
![]()
Nous allons étudier maintenant la logique négative et le théorème de DE MORGAN sur une autre page afin de ne pas encombrer celle-ci.
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente |
 Page suivante Page suivante |
Nombre de pages vues, à partir de cette date : le 15 JUILLET 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.