 Les Multiplexeurs |
Bas de page |
Les Comparateurs Binaires - Les Multiplexeurs :
2. - LES COMPARATEURS BINAIRES
Un comparateur binaire est un circuit logique qui effectue la comparaison entre 2 nombres binaires généralement notés A et B.
Il possède 3 sorties notées A = B, A > B et A < B qui indiquent le résultat de la comparaison comme suit :
Si le nombre A
est égal au nombre
B (A
= B), la sortie A = B passe à l'état
1 tandis que les sorties
A
> B et A < B passent à l'état
0.
Si le nombre A
est strictement supérieur au nombre B,
seule la sortie
A > B passe à l'état
1.
Si le nombre A
est strictement inférieur au nombre B,
seule la sortie
A < B passe à l'état
1.
Nous allons voir comment réaliser à l'aide de portes logiques un comparateur de 2 chiffres binaires.
2. 1. - COMPARATEUR DE DEUX CHIFFRES BINAIRES
Soit à comparer les deux chiffres binaires A et B. Examinons les cas où A = b, A > B et A < B.
Les deux nombres A et B sont égaux si
A = B = 1 ou
A = B = 0. La sortie
A = B doit donc passer à
l'état 1 uniquement pour ces deux
combinaisons. Son équation est donc A . B
+ 
. 
.
Le nombre A est strictement supérieur au
nombre B seulement si A = 1 et
B = 0. La sortie
A > B
doit donc passer à l'état 1 uniquement
pour cette combinaison. Son équation est donc A.
Le nombre A est strictement inférieur au
nombre B seulement si A = 0
et B = 1. La sortie
A < B
doit donc passer à l'état 1
uniquement
pour cette combinaison. Son équation B.
Toutes ces considérations sont traduites dans la table de vérité de la figure 19.
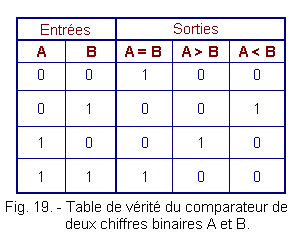
Reprenons l'équation de la sortie A
= B, AB + .
Nous savons que AB +
+ A
+ B
= 1 car quel que soit les états de A et B, l'une des quatre combinaisons vaut
1.
Nous en déduisons que AB +
est le complément logique de A
+ B
puisque la somme logique de ces deux expressions est 1.
Donc, AB +
= A
+ B.
Nous sommes ainsi conduits au schéma logique de la figure 20 qui fournit les trois signaux A < B, A = B et A > B à partir des bits A et B.
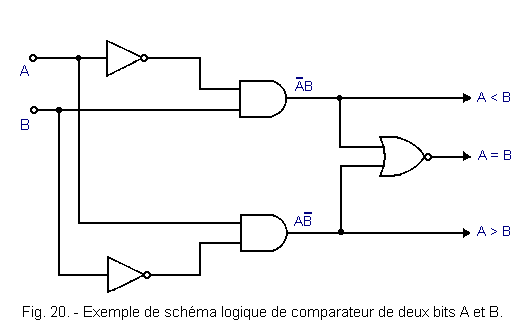
2. 2. - ANALYSE D'UN COMPARATEUR INTÉGRÉ : LE 7485
Le circuit intégré 7485 est un comparateur 4 bits, c'est-à-dire qu'il effectue la comparaison de deux nombres de 4 bits.
De plus, il dispose de 3 entrées notées A = B, A > B et A < B qui autorisent la mise en cascade de plusieurs circuits comparateurs du même type.
Ainsi, on peut comparer des nombres de 8, 12, 16 bits....
Le brochage de ce circuit est donné à la figure 21, tandis que la figure 22 représente son schéma logique.
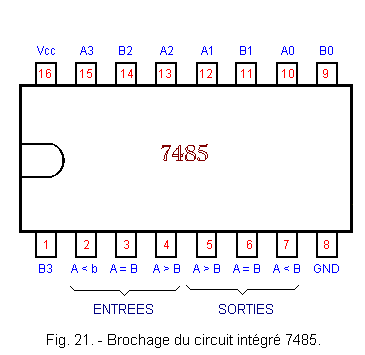
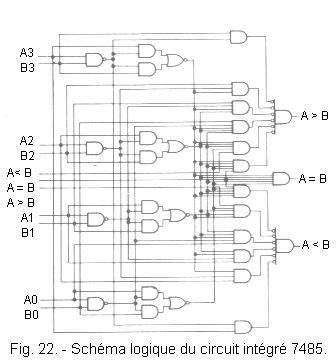
Avec ce circuit, on compare le nombre A composé des bits A3, A2, A1 et A0 (A3 = MSB et A0 = LSB) avec le nombre B composé des bits B3, B2, B1 et B0 (B3 = MSB et B0 = LSB).
La table de vérité de la figure 23 met en évidence l'action des entrées A > B, A < B et A = B.
Si l'on souhaite que la sortie
A
= B passe à l'état
1 chaque
fois que les deux nombres binaires sont égaux, il suffit de porter l'entrée A
= B à l'état 1, l'état des
entrées A < B et
A > B n'ayant alors pas d'importance.
Si l'on souhaite que la sortie
A
> B passe à l'état 1 également
dans le cas où les deux nombres binaires sont égaux, il suffit de porter
l'entrée A > B à l'état
1 et de porter les entrées A < B
et A = B à l'état
0.
Dans cette configuration de l'état des entrées A > B, A < B et A = B, la sortie A > B est à l'état 1 lorsque le nombre binaire A est supérieur au nombre binaire B ou quand ces deux nombres sont égaux. Elle indique donc si A ³ B.
De même, en portant l'entrée A
< B à l'état 1 et les entrées
A > B et
A = B
à l'état 0, la sortie A
< B indique le nombre binaire A
est inférieur ou égal au nombre binaire B.
En mettant en série deux comparateurs 7485, on peut comparer deux nombres de 8 bits. Il suffit de relier la sortie A = B du premier comparateur à l'entrée correspondante du second et de faire de même avec les sorties A > B et A < B. Les liaisons à effectuer sont indiquées à la figure 24.
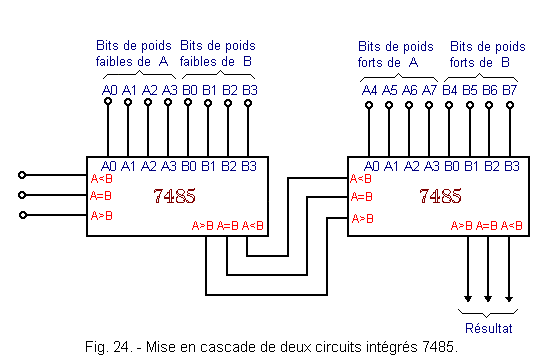
Ainsi, on compare le nombre A formé des 8 bits A7 à A0 (A7 = MSB et A0 = LSB) et le nombre B formé des 8 bits B7 à B0 (B7 = MSB et B0 = LSB).
Le premier circuit compare les poids faibles de A avec le poids faibles de B. Le résultat de cette comparaison est transmis aux entrées A < B, A = B et A > B du deuxième circuit.
Celui-ci compare les poids forts de A avec les poids forts de B et, en fonction du résultat de la comparaison des bits de poids faibles de A et B, indique sur ses sorties A > B, A = B et A < B le résultat de la comparaison des nombres A et B.
3. - LES MULTIPLEXEURS
Dans ce chapitre, nous allons examiner des circuits logiques très utilisés pour aiguiller des données : les multiplexeurs.
Ces circuits possèdent plusieurs entrées de données et une seule sortie.
A l'aide d'une ou plusieurs entrées de commande, on aiguille une des entrées de données vers la sortie. La sortie «recopie» l'entrée sélectionnée.
Un multiplexeur peut être comparé à un commutateur mécanique. Le nombre des entrées de données d'un multiplexeur définit le nombre de voies d'un multiplexeur. Si un multiplexeur possède n entrées de données, on dit qu'il s'agit d'un multiplexeur à n voies.
Le nombre des entrées de commande est fonction du nombre de voies du multiplexeur. Par exemple pour un multiplexeur à 4 voies, on a besoin de 2 entrées de commande. En effet, avec 2 entrées de commande, on peut former 2² = 4 combinaisons logiques distinctes pour différencier les 4 voies du multiplexeur. Un multiplexeur à 8 voies exigerait 3 entrées de commande puisque 23 = 8.
Examinons le plus simple des multiplexeurs, celui à 2 voies.
3. 1. - LE MULTIPLEXEUR A 2 VOIES
La figure 25 donne le schéma symbolique et l'équivalent mécanique d'un multiplexeur à 2 voies.
Suivant l'état de l'entrée de sélection A, la sortie S recopie soit l'entrée D0, soit l'entrée D1.
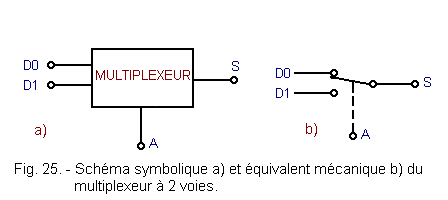
Supposons que pour A = 0, S = D0 et que pour A = 1, S = D1.
Nous en déduisons l'équation de S suivante :
S = D0
+ D1A
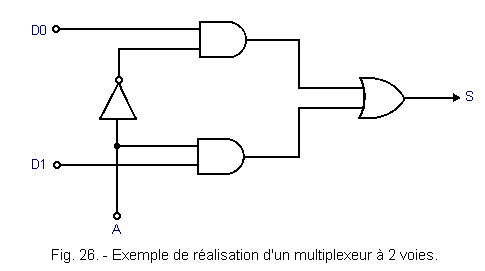
Le réseau combinatoire de la figure 26 peut fournir le signal S.
3. 2. - ANALYSE D'UN MULTIPLEXEUR À DEUX VOIES INTÉGRÉ : LE 74157
Le circuit intégré 74157 est un quadruple multiplexeur à 2 voies à entrée de sélection commune. L'entrée de validation (STROBE), également commune, force les quatre sorties au niveau L quand elle est soumise au niveau H.
Le brochage et le schéma logique de ce circuit sont donnés à la figure 27.
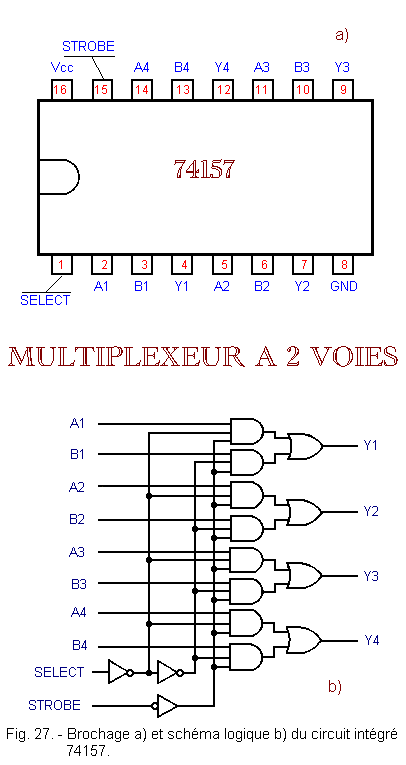
La table de vérité de la figure 28 montre que la donnée Ai est transférée en Yi lorsque l'entrée SELECT est à l'état 0. Lorsque cette entrée est à l'état 1, c'est la donnée Bi qui est transférée en Yi.
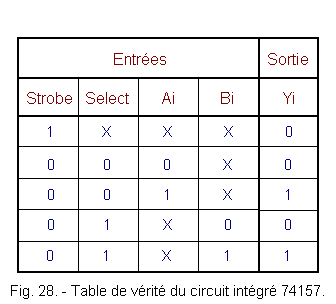
Considérons la donnée A constituée des bits A1, A2, A3 et A4, la donnée B constituée des bits B1, B2, B3 et B4 et la donnée Y constituée des bits Y1, Y2, Y3 et Y4.
En fonctionnement normal, l'entrée STROBE est maintenue à 0.
Si l'entrée SELECT est à l'état 0, la donnée Y est égale à la donnée A.
Si l'entrée SELECT est à l'état 1, la donnée Y est égale à la donnée B.
Un multiplexeur peut donc aiguiller des données constituées de plusieurs bits.
3. 3. - LE MULTIPLEXEUR A QUATRE VOIES
La figure 29 représente le schéma symbolique et l'équivalent mécanique d'un multiplexeur à 4 voies.
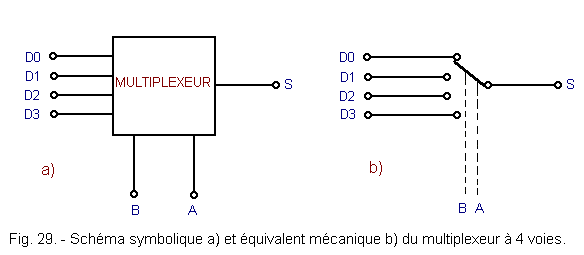
Le multiplexeur dispose de deux entrées de commande A et B pour sélectionner une des quatre entrées D0, D1, D2 ou D3.
En général, l'entrée sélectionnée porte en indice l'état correspondant à la combinaison des entrées de commande. Cela est traduit dans le tableau de la figure 30.
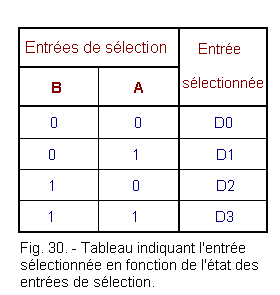
De ce tableau, on peut extraire l'équation de la sortie S suivante :
S =
.
. D0 +
. A . D1 + B .
. D2 + B . A . D3
On aboutit au schéma logique de la figure 31.
.gif)
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
 Haut de page |
|
Page précédente |
 Page suivante |
Nombre de pages vues, à partir de cette date : le 15 JUILLET 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.