Les Réseaux Logiques Programmables Les Réseaux Logiques Programmables |
 Les PLA "Programmable Logic Array" Les PLA "Programmable Logic Array"
|
 Les FPLA Les FPLA
|
 FPLA avec Mémoire FPLA avec Mémoire
|
 Bas de page Bas de page |
Les Réseaux Logiques Programmables - "PLA" - Les FPLA :
Dans la théorie précédente, nous avons vu l'utilisation que nous pouvions faire des mémoires ROM, pour remplacer un circuit combinatoire formé généralement avec des portes logiques NAND, NOR,....
Cette évolution technologique en direction des circuits programmables, déjà relevée lors de l'examen des multiplexeurs, a conduit les fabricants de circuits intégrés à réaliser d'autres dispositifs logiques programmables connus sous l'appellation PLA (Programmable Logic Array).
Les PLA, ainsi que les multiplexeurs, démultiplexeurs et les mémoires micro-électroniques, sont le résultat des technologies récentes d'intégration, lesquelles ont également conduit à la conception et à la réalisation de circuits très complexes tels que les microprocesseurs et leurs circuits associés.
Cette évolution vers les circuits à haut niveau d'intégration a également posé de nouveaux problèmes liés à l'assemblage des circuits intégrés entre eux et à leur interfaçage qui est l'ensemble des principes et des techniques permettant de relier plusieurs systèmes électroniques entre eux.
Dans cette théorie, nous donnerons une vue générale sur ces circuits récents, ainsi que sur l'ensemble des problèmes qui s'y rattachent.
![]() 1. - LES RÉSEAUX LOGIQUES PROGRAMMABLES
1. - LES RÉSEAUX LOGIQUES PROGRAMMABLES
1. 1. - LES CIRCUITS INTÉGRÉS COMPLEXES
Le niveau d'intégration des circuits ne cesse de s'accroître et l'on s'accorde à reconnaître les catégories de circuits intégrés suivantes :
![]() S.S.I.
(Short
Scale
Integration) : 1 à 10 transistors par circuit intégré.
S.S.I.
(Short
Scale
Integration) : 1 à 10 transistors par circuit intégré.
![]() M.S.I.
(Medium
Scale
Integration) : 10 à quelques centaines de
transistors.
M.S.I.
(Medium
Scale
Integration) : 10 à quelques centaines de
transistors.
![]() L.S.I.
(Large
Scale Integration) : de quelques centaines à
10 000 transistors.
L.S.I.
(Large
Scale Integration) : de quelques centaines à
10 000 transistors.
![]() V.L.S.I.
(Very
Large
Scale
Integration) : plus de 10 000
transistors.
V.L.S.I.
(Very
Large
Scale
Integration) : plus de 10 000
transistors.
L'évolution des circuits intégrés a été telle que le coût par transistor intégré s'est réduit au cours des vingt dernières années à un millionième de celui initial.
Il est désormais possible de concentrer sur un seul circuit intégré tout un ensemble de fonctions logiques autrefois réalisées par plusieurs circuits intégrés. Pensez par exemple aux calculatrices de bureau : vers la fin des années soixante, on a commencé à les construire avec plusieurs dizaines de circuits S.S.I. et M.S.I. ; aujourd'hui, un seul circuit intégré L.S.I. effectue toutes les opérations nécessaires.
C'est parce que ces calculatrices peuvent être diffusées à plusieurs dizaines de milliers d'exemplaires qu'il est apparu plus avantageuse de concevoir et de produire un seul circuit intégré regroupant toutes les fonctions de la calculatrice.
Généralement, le constructeur achète le ou les circuits intégrés nécessaires, les accessoires mécaniques, électriques, les afficheurs et procède à l'assemblage final de ces différents éléments pour construire ces calculatrices.
La même procédure est habituellement suivie pour la fabrication des montres digitales.
Pour une production en petite série, un fabricant peut employer d'autres méthodes, en particulier utiliser des composants standards.
Le facteur déterminant est la quantité d'un produit donné qui sera écoulée sur le marché. En général, quand cette quantité est assez importante, le constructeur fait réaliser un circuit approprié (ou plusieurs) par un fabricant de circuits intégrés.
Ces circuits intégrés sont appelés CUSTOM (client), car ils sont développés à la demande d'un client bien précis.
Le premier microprocesseur a été créé de cette façon.
Pour une production en petite série, la solution la plus économique consiste à utiliser les composants standards disponibles sur le marché. Dans certains cas, il existe plusieurs solutions pour réaliser une fonction. Par exemple, on peut soit concevoir un réseau combinatoire, soit utiliser des ROM ou des multiplexeurs, comme cela a été indiqué dans les théories précédentes.
En règle générale, il est préférable d'utiliser des circuits intégrés plus complexes en nombre restreint plutôt qu'une grande quantité de circuits intégrés moins complexes. En effet, le coût de revient d'un circuit complexe (par exemple L.S.I.) est à peine plus élevé que celui d'un circuit simple (S.S.I.).
Il faut noter, par ailleurs, qu'un circuit L.S.I. peut être nettement plus cher qu'un circuit S.S.I. dans la première phase de production de ce circuit car le coût est directement lié à la quantité produite. Comme l'indique la figure 1, le prix de revient diminue très rapidement quand la production augmente.
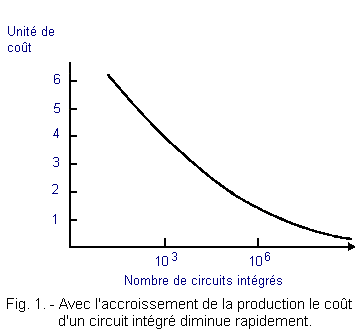
Les circuits intégrés complexes présentent donc plusieurs avantages ; ils peuvent remplacer plusieurs circuits intégrés moins complexes, ils permettent de réduire la dimension des circuits imprimés, de faciliter les opérations de montage et finalement de diminuer le prix de revient.
Nous pouvons noter également que dans le coût global d'un système microélectronique, le prix des circuits intégrés représente environ 10 % du montant total, les 90 % restants se répartissant entre les différents postes suivants :
-
Circuit imprimé,
-
Connecteurs,
-
Insertion et soudure des circuits intégrés,
-
Liaisons,
-
Alimentation,
-
Châssis,
-
Condensateurs de découplage,
-
Essai du système,
A ce coût de fabrication s'ajoutent les frais relatifs à l'étude du système électronique, au stockage des produits finis et des composants du système, à l'administration, etc...
Il a été calculé que la somme de tous les frais, dans le cas d'un système numérique moyen, est égale à environ vingt fois le coût des circuits intégrés composant ce système. Si par exemple, le prix du composant est d'un euro, le prix de revient global sera de vingt euros.
Donc le coût total d'un système est fonction du nombre de circuits intégrés qui le composent même s'il n'est pas directement proportionnel à celui-ci.
Sur le graphique de la figure 2, on voit qu'un système composé de 200 circuits intégrés coûte 2 unités et que celui nécessitant 800 circuits intégrés revient à 4 unités.
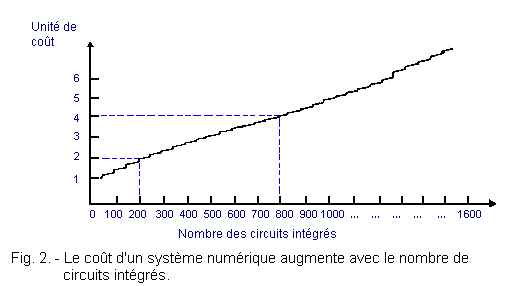
Le nombre de circuits intégrés est multiplié par 4 alors que le coût du système double seulement.
Si maintenant les deux systèmes étaient intégrés en un seul circuit, leurs coûts globaux seraient à peu près équivalents puisque les deux circuits intégrés reviendraient pratiquement au même prix.
Ces différentes notions sont bien connues des producteurs de circuits intégrés ainsi que de leur clientèle. Néanmoins, il existe un inconvénient : les circuits intégrés complexes sont très spécialisés et très variés. Par conséquent, ils sont généralement produits en quantité plus faible que les circuits standards.
Sous la pression de ces différents problèmes, on a cherché à concevoir des circuits à haut niveau d'intégration, mais qui puissent remplir des fonctions très variées. Ceci a conduit à la conception des PLA ou Réseaux Logiques Programmables.
![]() 1. 2. - LES RÉSEAUX
LOGIQUES PROGRAMMABLES (PLA)
1. 2. - LES RÉSEAUX
LOGIQUES PROGRAMMABLES (PLA)
Les PLA ont
été conçus en partant du principe que toute fonction logique peut être écrite
sous la forme d'une somme de mintermes (forme
canonique). Soit par exemple la fonction : F = ![]() bd
+ ab
bd
+ ab![]()
![]() + a
+ a![]() cd.
cd.
Cette fonction est la somme des trois
mintermes suivants : ![]() bd,
ab
bd,
ab![]()
![]() et a
et a![]() cd.
cd.
Les PLA permettent de générer un certain nombre de mintermes à partir de n variables et d'effectuer la somme de ces mintermes.
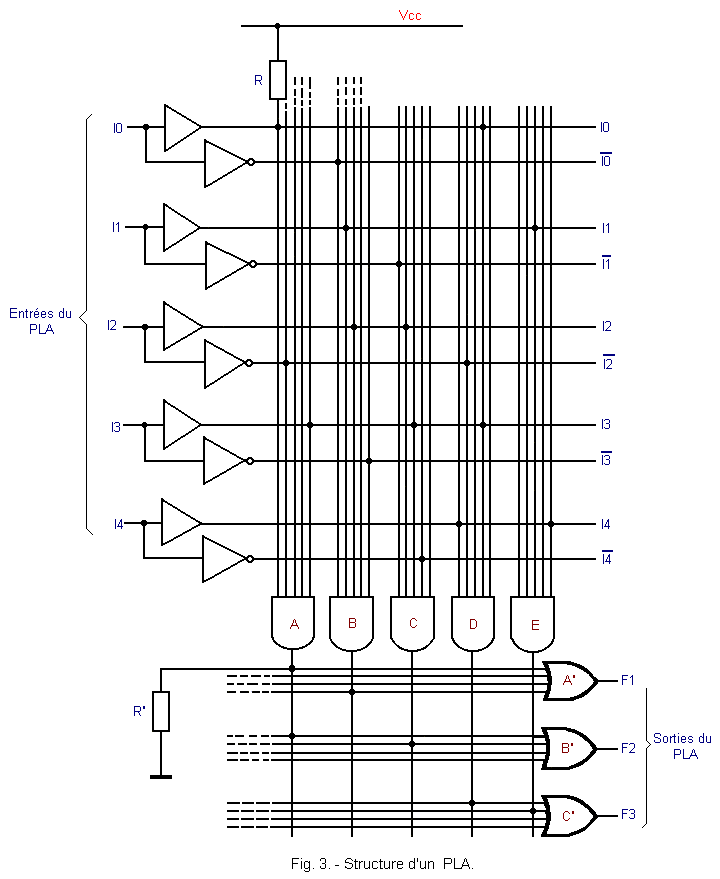
La figure 3 représente la structure fondamentale d'un PLA.
Chaque porte ET (A, B, C, D, E) à cinq entrées permet de générer un minterme à partir des cinq variables d'entrée (I0, I1, I2, I3, I4).
Chaque porte OU (A', B', C') à quatre entrées permet d'effectuer la somme des mintermes nécessaires à l'obtention d'une fonction logique définie.
Le circuit est disposé en forme de matrice avec des liaisons horizontales et verticales.
Dans la partie supérieure, les lignes horizontales représentent les entrées I0, I1, I2, I3 et I4 du PLA et les lignes verticales correspondent aux entrées des portes ET.
Initialement, les lignes horizontales et verticales se croisent sans contact entre elles. La programmation consistera ultérieurement à réunir une ligne horizontale avec une ligne verticale en un point de jonction symbolisé sur la figure 3 par un point.
L'état logique de la sortie d'une porte ET correspond donc à la valeur d'un minterme.
Il suffira, lors de la programmation, de réunir les sorties des portes ET que l'on souhaite aux entrées des portes OU afin de réaliser la somme logique de ces mintermes.
Dans l'exemple de la figure 3, on a «créé» ainsi trois réseaux combinatoires ; leurs sorties respectives étant les trois sorties F1, F2 et F3.
Le circuit ayant pour sortie F1 est formé avec la porte OU (A') et avec les portes ET A et B ; celui ayant pour sortie F2 est formé avec les portes B', A et C ; enfin, celui ayant pour sortie F3 est formé avec les portes C', D et E.
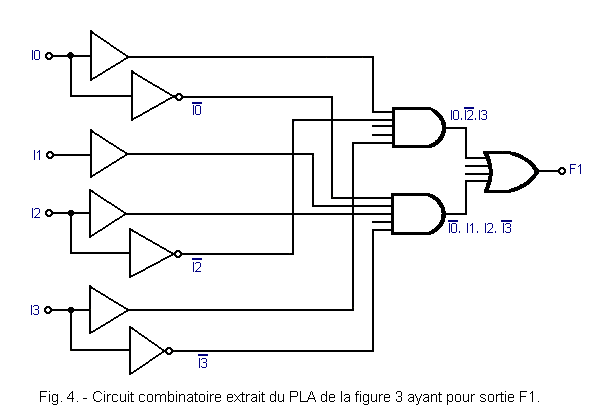
La figure 4 représente le premier de ces trois circuits combinatoires.
La fonction logique F1 s'écrit :
![]()
En règle générale, la programmation d'un PLA est effectuée par le constructeur à partir des données fournies par le client.
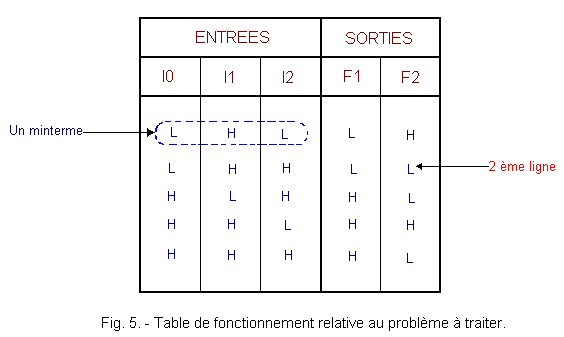
Ce dernier, peut par exemple, fournir une table de fonctionnement relative au problème é résoudre.
Nous allons examiner un exemple volontairement simple à partir du tableau situé figure 5.
Il est nécessaire de constituer cinq mintermes. Il faut donc au minimum cinq portes ET à trois entrées (il y a trois variables). Il faut également deux portes OU puisqu'il y a deux fonctions (F1 et F2) à générer.
Le PLA programmé pour répondre au problème posé est donné figure 6.
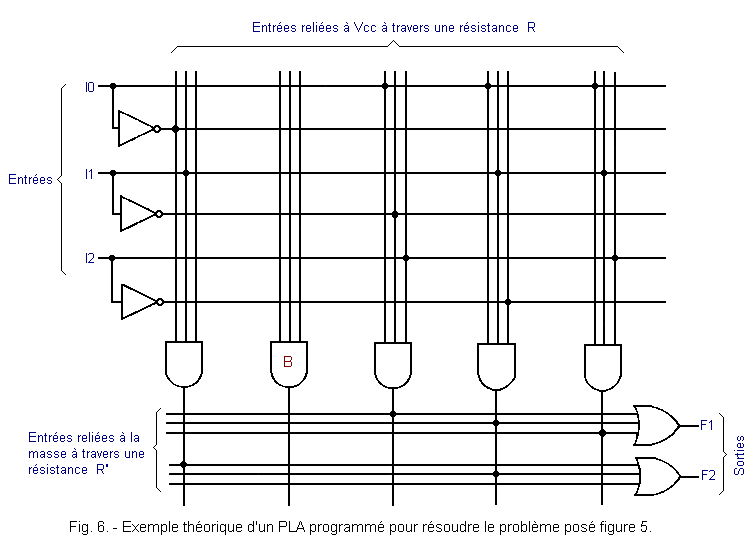
Vous remarquez que le ET noté B n'est pas utilisé. En effet, dans la table de fonctionnement de la figure 5, à la deuxième ligne, vous constatez que les deux sorties F1 et F2 sont à l'état L, donc il n'est pas nécessaire de câbler les entrées de la porte B.
Finalement, quatre portes ET sont suffisantes pour résoudre le problème posé.
Il serait possible de résoudre ce problème en utilisant une ROM. Théoriquement, il faudrait une ROM possédant trois entrées et deux sorties soit une mémoire ROM dont la capacité serait de 23 (combinaisons possibles avec trois entrées) multipliée par 2 (nombre de sorties), soit 8 x 2 = 16 bits.
Dans le cas d'un PLA, on définit la capacité de matrice qui est égale au produit du nombre de portes ET par le nombre de portes OU. Cette capacité s'exprime en bits. Dans le cas présent, elle est de 4 x 2 = 8 bits.
L'avantage du PLA par rapport à la ROM est manifeste si l'on considère un PLA à 14 entrées et 8 sorties, disponible sur le marché.
Considérons un PLA comportant 96 portes ET, ce qui permet déjà de nombreuses possibilités, par exemple la constitution de 96 mintermes. La capacité de matrice de ce PLA est égale à 96 x 8 = 768 bits.
Une ROM équivalente devrait avoir une capacité de 214 x 8 = 131 072 bits.
Un PLA est donc beaucoup plus avantageux qu'une ROM. En effet, dans le cas de cette dernière, il faut tenir compte de toutes les combinaisons possibles des entrées : avec 14 entrées, il faut donc une ROM avec 214 = 16 384 adresses, tandis qu'avec un PLA on ne s'intéresse qu'aux combinaisons données par la table de fonctionnement qui sont nécessaires pour résoudre le problème.
![]() 1. 3. - LES
FPLA
1. 3. - LES
FPLA
Comme les constructeurs ont conçu et produit les PROM après les ROM, les FPLA (Field Programmable Logic Array = réseaux logiques programmables par fusibles) sont apparus après les PLA.
Leur principe reste le même que celui des PLA. Les FPLA sont facilement programmables par l'utilisateur. Il suffit pour cela de posséder un appareil à programmer qui est souvent un simple programmateur de PROM.
Le principe de la programmation de ces FPLA consiste à faire fondre des fusibles aux endroits adéquats en les faisant traverser par une brève surintensité de courant, exactement comme l'on procède avec les mémoires PROM.
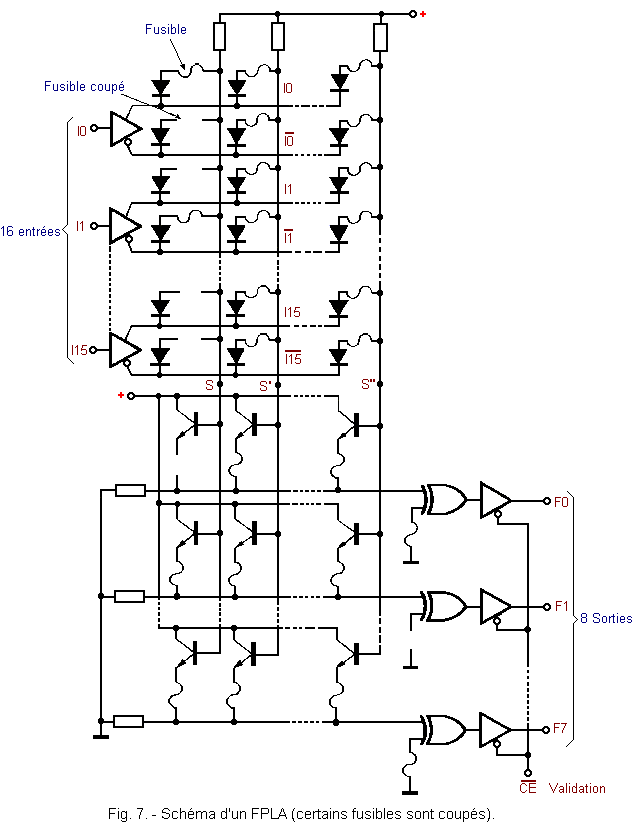
La figure 7 représente le schéma
d'un FPLA déjà programmé. Les fusibles
sont représentés par le symbole ![]() .
.
Le FPLA représenté possède 16 entrées notées I0 à I15 et 8 sorties notées F0 à F7.
Pour chaque entrée du FPLA, il y a deux lignes horizontales ; le signal présent sur l'une étant complémentaire de celui présent sur l'autre, ainsi que l'indique le symbole suivant :
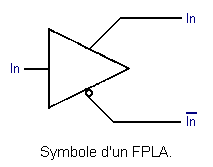
Le point S (ainsi que S', S"...) est la sortie d'un ET constitué par des diodes en parallèle.
Si l'on veut représenter le premier ET de FPLA, on obtient le schéma de la figure 8.
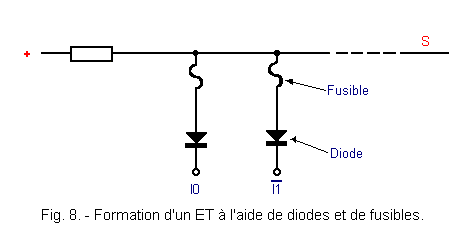
Ce premier minterme peut s'écrire ainsi :
S = I0 . ![]() 1
1
De la même façon, le deuxième minterme (sortie S') s'écrira :
S' = I0 . ![]() 0
. I1 .
0
. I1 . ![]() 1...
I15 .
1...
I15 . ![]() 15
15
Il est bien évident que S' = 0 pour toutes les combinaisons des variables d'entrée.
Les OU sont constitués par des transistors en parallèle. Le premier OU correspondant à la sortie F0 peut être représenté comme indiqué figure 9.
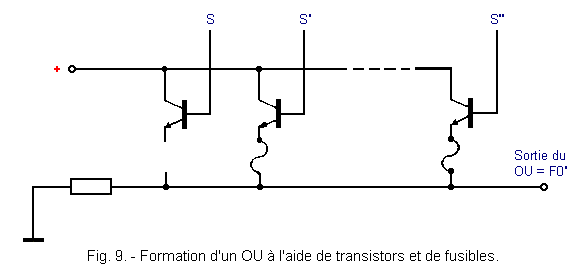
La sortie F0' du OU est égale à F0' = S' + S".
La porte OU Exclusif permet d'inverser le signal de sortie du OU correspondant. Il suffit pour cela de faire fondre le fusible et cette entrée se trouve alors au niveau logique H. C'est le cas de la sortie F1 (figure 7).
Exemple :
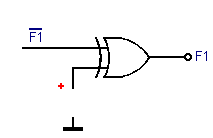
Il existe une entrée de commande
notée ![]() (initiales de
Chip
Enable = validation de boîtier). Elle valide
les huit sorties quand elle est au niveau
L.
Par contre, quand cette entrée est au niveau
H,
les huit sorties sont à l'état haute impédance (sorties tri-state).
(initiales de
Chip
Enable = validation de boîtier). Elle valide
les huit sorties quand elle est au niveau
L.
Par contre, quand cette entrée est au niveau
H,
les huit sorties sont à l'état haute impédance (sorties tri-state).
![]() 1. 4. - FPLA AVEC
MÉMOIRE
1. 4. - FPLA AVEC
MÉMOIRE
Un autre type de réseau logique s'est également développé, le FPLA avec mémoire.
Ce FPLA possède un registre, généralement constitué par un ensemble de bascules synchrones de type RS.
Ce registre permet l'implantation dans le FPLA d'un circuit logique séquentiel. L'état des sorties est à la fois fonction de l'état des entrées et de l'état logique des sorties avant le front d'horloge.
Le synoptique de la figure 10 représente un FPLA avec mémoire.
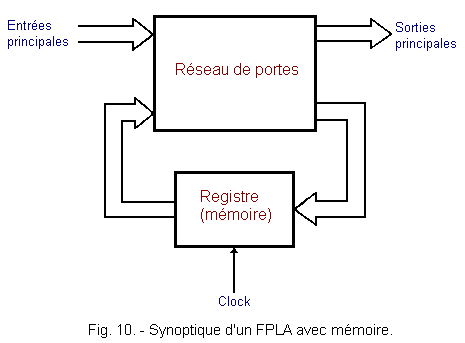
Grâce au registre, les données présentes en sortie du FPLA sont réintroduites à l'entrée du réseau de portes au front d'horloge suivant.
Le schéma de la figure 11 est un synoptique plus développé d'un FPLA avec mémoire appelé FPLS (Field Programmable Logic Sequencer).
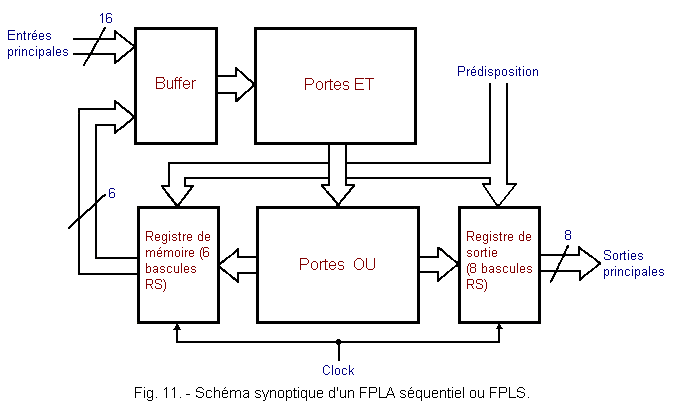
Le buffer est un ensemble logique qui recueille à la fois les données présentes sur les 16 entrées principales et sur les 6 sorties du registre de mémorisation.
Le registre de sortie sert à maintenir les données entre deux impulsions d'horloge.
On retrouve par ailleurs le réseau de portes ET et OU caractéristique des PLA.
1. 5. - GATE ARRAY
Parfois, les PLA décrits dans les paragraphes précédents, sont inadaptés pour résoudre certains problèmes ; soit qu'ils ne soient pas suffisamment souples d'emploi, soit qu'il faille réaliser un nombre important de circuits assez complexes.
Une première solution consiste à concevoir des customs ou circuits intégrés spécifiques.
Une seconde solution consiste à utiliser des circuits dont le principe est intermédiaire entre celui des PLA et celui des customs et que l'on nomme Gate Array (réseau de portes logiques) ou encore FPGA (Field Programmable Gate Array).
Ces circuits sont constitués d'un nombre important de portes NAND situé généralement entre 500 et 2 000.
La technologie employée est, soit la technologie TTL S (Schottky), soit la technologie CMOS.
La programmation consiste à relier entre elles des portes NAND afin de constituer le réseau logique adéquat.
L'avantage du Gate Array réside dans le fait qu'on peut le produire à grande échelle pour des applications variées.
Un circuit intégré de ce type peut remplacer jusqu'à 50 circuits intégrés S.S.I. et M.S.I.
Le
Gate
Array,
comme le
PLA
est programmé
par le constructeur à partir du problème spécifique proposé par le client.
Tous les circuits que nous venons de voir, FPLA, FPLS,
et FPGA
sont parfois appelés
IFL
(Integrated
Fuse
Logic = logique par
fusibles intégrés).
 Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. Cliquez ici pour la leçon suivante ou dans le sommaire prévu à cet effet. |
|
 Page précédente Page précédente |
 Page suivante Page suivante |
Nombre de pages vues, à partir de cette date : le 15 JUILLET 2019
Envoyez un courrier électronique à Administrateur Web Société pour toute question ou remarque concernant ce site Web.
Version du site : 10. 4. 12 - Site optimisation 1280 x 1024 pixels - Faculté de Nanterre - Dernière modification : 02 Septembre 2016.
Ce site Web a été Créé le, 14 Mars 1999 et ayant Rénové, en Septembre 2016.